Enchaînons sur la série GT avec les strip plot. Il s’agit ici, non plus comme avec les histogrammes de figurer les observations au travers d’objets dont la taille et la forme varie en fonction de la fréquence d’une valeur, mais plus directement de montrer les données. Pour ce faire, chaque observation est représentée par un point placé en fonction de sa valeur le long d’un axe vertical ou horizontal unique. Les différents points sont ainsi amenés à se rapprocher ou s’éloigner les uns des autres en fonction de la dispersion des valeurs. Une accumulation de points sur l’axe à un endroit donné marque l’importance de la fréquence d’une valeur sur la distribution. Pour les mettre en valeur les points, et/ou simplement éviter que l’ensemble apparaisse trop peu lisible, il est utile sur un strip plot de jouer sur les couleurs ou les degrés de transparence, voire sur les positions des points sur la dimension ne servant pas à marquer les valeurs par exemple en les y plaçant de manière aléatoire. Les possibilités sont multiples. Il sera d’autant plus important de les mettre en oeuvre que le nombre d’observations est important.
Pour l’illustration, restons sur l’effet weekend sur lequel nous avons travaillé dans le précédent post. Mais avant d’aller plus loin, rappelons rapidement ce dont il s’agit.
Dans les années 80-90, une série d’études est venue mettre en évidence la présence de régularités dans les rendements des actions. Ces constats sont en contradiction avec l’hypothèse d’efficience des marchés financiers qui était à l’époque centrale en Finance (depuis la Finance comportementale a fait son chemin). Cette hypothèse postule notamment que les rendements ne sont pas systématiquement prévisibles. Il ne devrait donc pas y avoir de régularité dans les rendements des titres. En fait, dans le cadre de l’efficience, seules les informations nouvelles concernant les perspectives de gains futures tirés des titres devraient affecter les prix. Le timing de ces nouvelles informations est aléatoire et donc tout régularité calendaire dans les rendements est une anomalie.
L’une des premières anomalie relevée, notamment par @french1980, concerne les rendements des lundi et de vendredi. Sur sa période d’étude, il constate des rendements en moyenne plus petits que les autres jours de la semaine les lundi et plus important les vendredi. Attention! Avant de vous précipiter, pour arbitrer l’anomalie et faire fortune, je tiens à préciser que, sur la plupart des marchés, cette anomalie n’est plus constatée. N’allons pas plus loin sur le sujet et commençons à travailler nos graphes.
Préalablement, comme toujours commençons par charger les packages qui nous serons utiles par la suite. Nous nous contenterons ici des seuls tidyverse, scales et tidyquant.
library(tidyverse)
library(scales)
library(tidyquant)Ceci fait, chargeons les données concernant l’indice Standard & Poor 500 à partir de la fonction tq_get(). Indiquons le ticker correspondant à titre de premier argument, “^GSPC”, ainsi que la période retenue pour l’analyse qui est ici 1954-2023. Visualisons le résultat via glimpse().
dat<-tq_get("^GSPC",from="1954-01-31", to = "2023-05-04")
glimpse(dat)## Rows: 17,434
## Columns: 8
## $ symbol <chr> "^GSPC", "^GSPC", "^GSPC", "^GSPC", "^GSPC", "^GSPC", "^GSPC"…
## $ date <date> 1954-02-01, 1954-02-02, 1954-02-03, 1954-02-04, 1954-02-05, …
## $ open <dbl> 25.99, 25.92, 26.01, 26.20, 26.30, 26.23, 26.17, 26.14, 26.06…
## $ high <dbl> 25.99, 25.92, 26.01, 26.20, 26.30, 26.23, 26.17, 26.14, 26.06…
## $ low <dbl> 25.99, 25.92, 26.01, 26.20, 26.30, 26.23, 26.17, 26.14, 26.06…
## $ close <dbl> 25.99, 25.92, 26.01, 26.20, 26.30, 26.23, 26.17, 26.14, 26.06…
## $ volume <dbl> 1740000, 1420000, 1690000, 2040000, 2030000, 2180000, 1880000…
## $ adjusted <dbl> 25.99, 25.92, 26.01, 26.20, 26.30, 26.23, 26.17, 26.14, 26.06…Nous ne travaillerons pas directement à partir des prix mais des rendements. Calculons-les à partir des prix ajustés (adjusted).
dat<-dat %>% select(date,adjusted) %>%
mutate(ret=adjusted/lag(adjusted)-1) %>%
drop_na()Marquons les jours de la semaine. Ajoutons les mois, trimestres et années que l’on pourra utiliser par la suite en compléments.
dat<-dat%>% mutate(day_of_the_week=wday(date),
day_lab=wday(date,label=TRUE,abbr=FALSE),
mois_lab=month(date,label=TRUE,abbr=FALSE),
trimestre=quarter(date),
annee=year(date)) %>%
select(date,day_of_the_week,day_lab,
mois_lab,trimestre,annee,ret)Maintenant que nos données sont prêtes, passons au graphe. La procédure est simple. Il s’agit d’utiliser le geom_point() en indiquant comme esthétique pour l’axe des abscisses day_lab et pour les ordonnées ret.
ggplot(data=dat,aes(x=day_lab,y=ret))+
geom_point()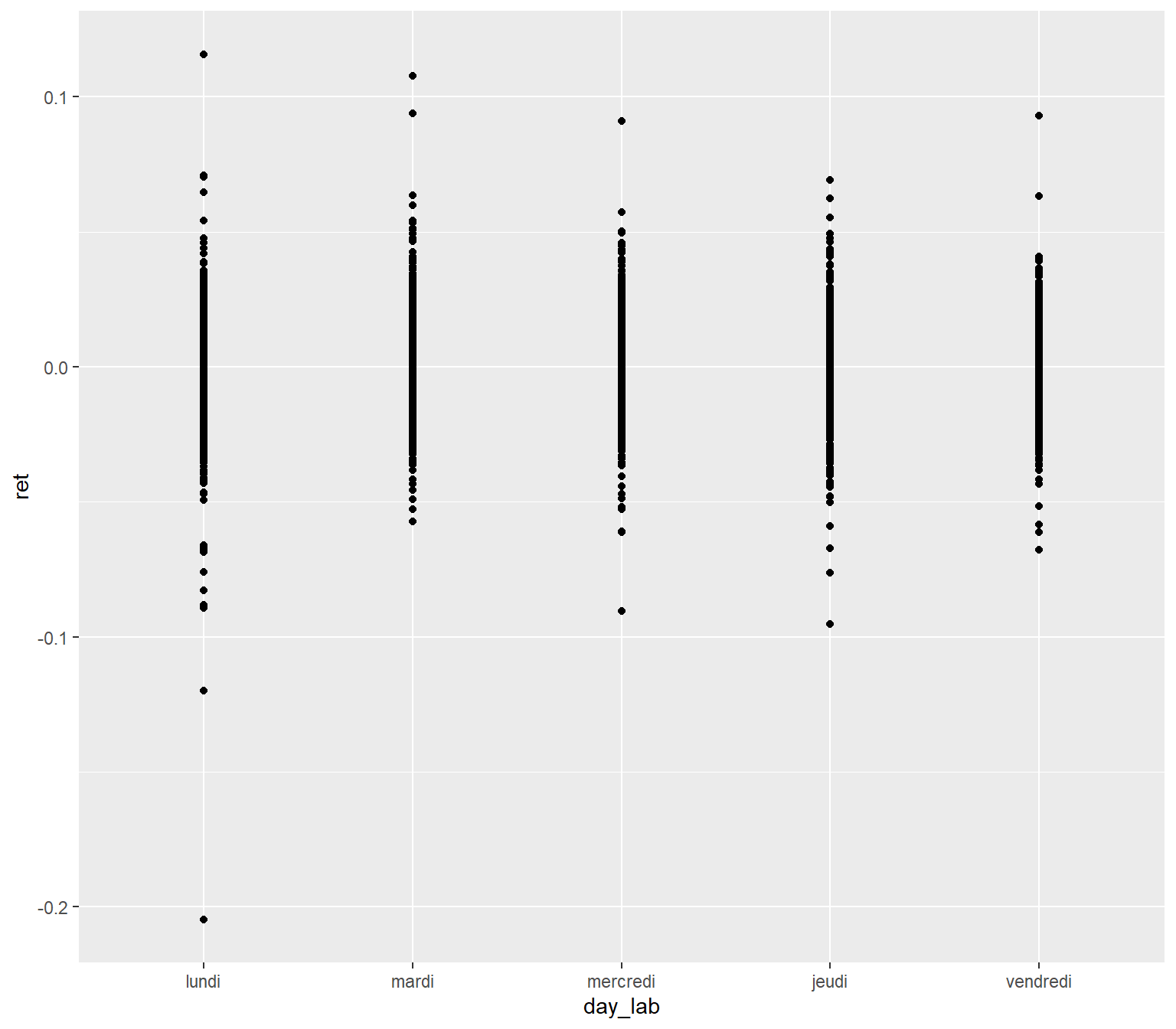
Cette représentation présente le défaut de superposer les points. Pour s’en convaincre, dénombrons les observations associées aux différents jours de la semaine.
dat %>% group_by(day_lab) %>%
count()## # A tibble: 5 × 2
## # Groups: day_lab [5]
## day_lab n
## <ord> <int>
## 1 lundi 3332
## 2 mardi 3559
## 3 mercredi 3553
## 4 jeudi 3507
## 5 vendredi 3482On est loin de voir les plus de trois milles points différents sur chaque jours de la semaines…
Essayons de faire ressortir de manière plus nette les différents points et profitons-en pour procéder à un peu de mise en forme. Commençons par réduire la taille des points et appliquons leur de la transparence (alpha).
ggplot(data=dat,aes(x=day_lab,y=ret))+
geom_point(alpha=0.25,size=1)+
labs(title="Rendement journaliers du S&P 500",
subtitle ="période 1954-2023",
caption="Source: données Yahoo! Finance")+
scale_y_continuous(labels = label_percent())+
theme_minimal()+
theme(
plot.title = element_text(hjust=0.5,face='bold'),
plot.subtitle = element_text(hjust=0.5,face='italic'),
plot.caption = element_text(hjust=1,face='italic'),
axis.title = element_blank(),
axis.line.y.left = element_line(color="black"),
)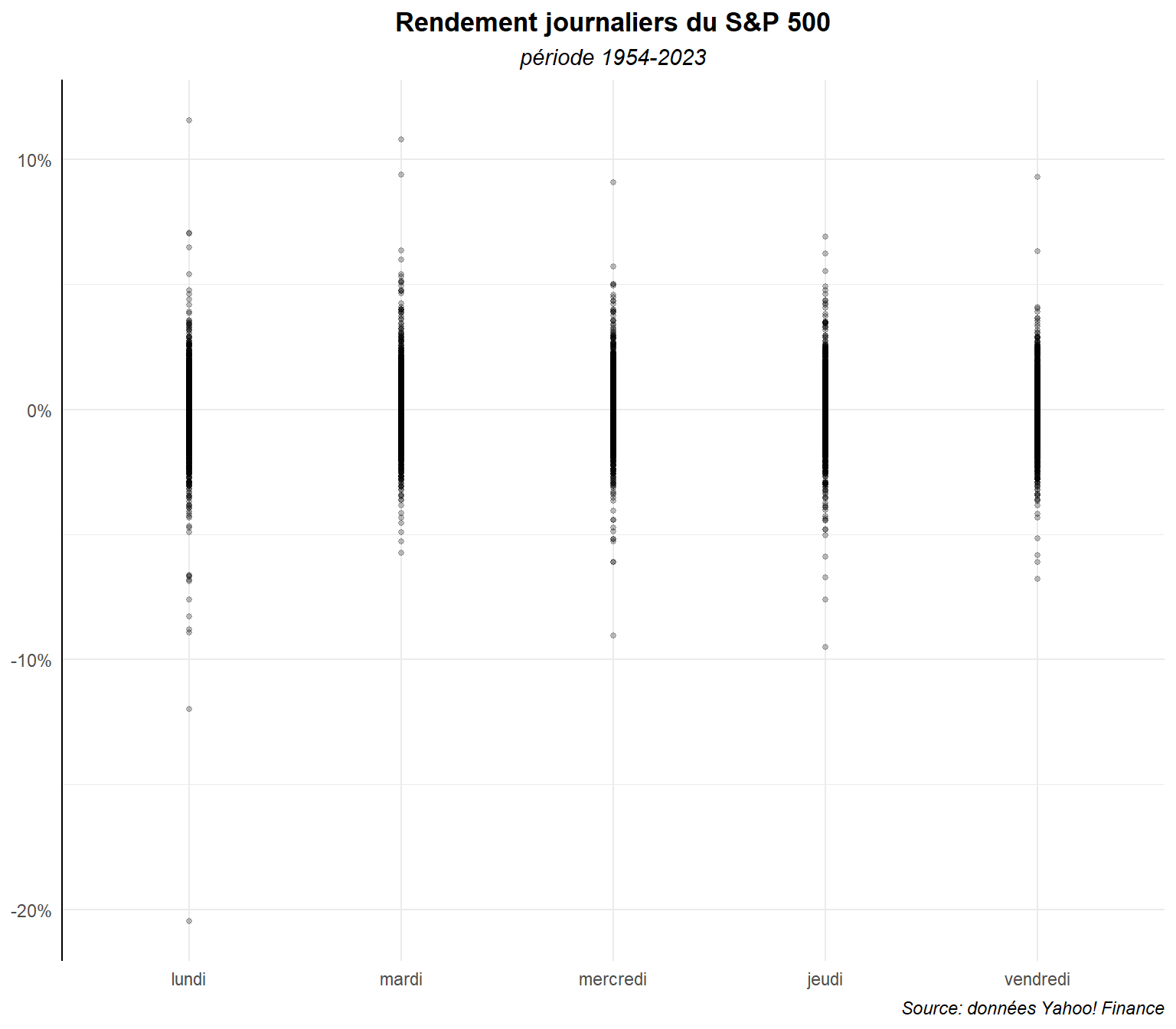
La transparence permet de mieux distinguer les différents degrés de regroupement d’observations. Les choses pourraient être plus signifiante si on ajoutait des repères. Plaçons sur le graphe des éléments marquant le rendement moyen sur la période globale et sur chaque jours. Cette moyenne est de :
mean(dat$ret)## [1] 0.0003414452Les moyennes pour chaque jours sont :
dat %>% group_by(day_lab) %>%
summarise(moyenne=mean(ret))## # A tibble: 5 × 2
## day_lab moyenne
## <ord> <dbl>
## 1 lundi -0.000523
## 2 mardi 0.000479
## 3 mercredi 0.000762
## 4 jeudi 0.000329
## 5 vendredi 0.000611Indiquons les en rouge sur le graphe.
ggplot(data=dat,aes(x=day_lab,y=ret,group=day_lab))+
geom_point(alpha=0.25,size=1)+
geom_hline(yintercept = mean(dat$ret), color='red')+
geom_text(aes(label="moyenne",x="lundi", y=0.01), color="red",
size=2,nudge_x=-0.35)+
stat_summary(fun=mean, geom="point",
size=1, color="red")+
labs(title="Rendement journaliers du S&P 500",
subtitle ="période 1954-2023",
caption="Source: données Yahoo! Finance")+
scale_y_continuous(labels = label_percent())+
theme_minimal()+
theme(
plot.title = element_text(hjust=0.5,face='bold'),
plot.subtitle = element_text(hjust=0.5,face='italic'),
plot.caption = element_text(hjust=1,face='italic'),
axis.title = element_blank(),
axis.line.y.left = element_line(color="black"),
)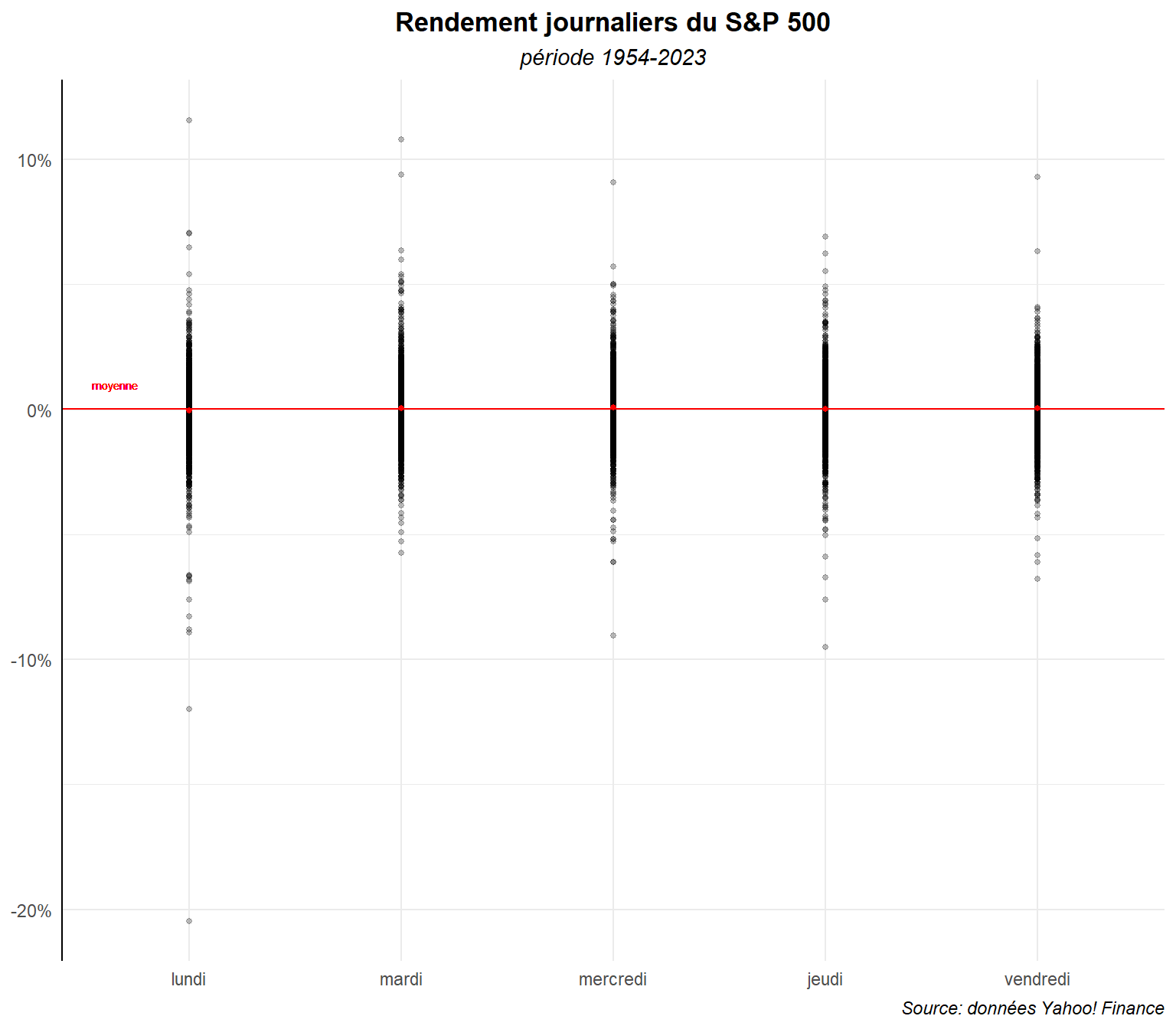
On voit clairement que les moyennes différents difficilement d’un jours à l’autre voir même de la moyenne sur l’ensemble de la période. Voyons rapidement ce qu’il en est sur la période étudiée par French (1980), autrement-dit 1953-1977.
ggplot(data=filter(dat,date>date("1953/01/01")&
date<date("1977/12/31")),
aes(x=day_lab,y=ret,group=day_lab))+
geom_point(alpha=0.25,size=1)+
geom_hline(yintercept = mean(dat$ret), color='red')+
geom_text(aes(label="moyenne",x="lundi", y=0.01), color="red",
size=2,nudge_x=-0.35)+
stat_summary(fun=mean, geom="point",
size=1, color="red")+
labs(title="Rendement journaliers du S&P 500",
subtitle ="période 1954-1977",
caption="Source: données Yahoo! Finance")+
scale_y_continuous(labels = label_percent())+
theme_minimal()+
theme(
plot.title = element_text(hjust=0.5,face='bold'),
plot.subtitle = element_text(hjust=0.5,face='italic'),
plot.caption = element_text(hjust=1,face='italic'),
axis.title = element_blank(),
axis.line.y.left = element_line(color="black"),
)
Le contraste est plus marqué mais l’ensemble reste confus. Voyons ce qu’il en est si on winsorise (si on enlève les observations les plus extrêmes, les 1% de valeurs plus grande et plus petite).
ggplot(data=filter(dat,date>date("1953/01/01")&
date<date("1977/12/31")&
ret>=quantile(ret,probs=.01)&
ret<quantile(ret,probs=.99)),
aes(x=day_lab,y=ret,group=day_lab))+
geom_point(alpha=0.25,size=1)+
geom_hline(yintercept = mean(dat$ret), color='red')+
geom_text(aes(label="moyenne",x="lundi", y=0.01), color="red",
size=2,nudge_x=-0.35)+
stat_summary(fun=mean, geom="point",
size=1, color="red")+
labs(title="Rendement journaliers du S&P 500",
subtitle ="période 1954-1977",
caption="Source: données Yahoo! Finance")+
scale_y_continuous(labels = label_percent())+
theme_minimal()+
theme(
plot.title = element_text(hjust=0.5,face='bold'),
plot.subtitle = element_text(hjust=0.5,face='italic'),
plot.caption = element_text(hjust=1,face='italic'),
axis.title = element_blank(),
axis.line.y.left = element_line(color="black"),
)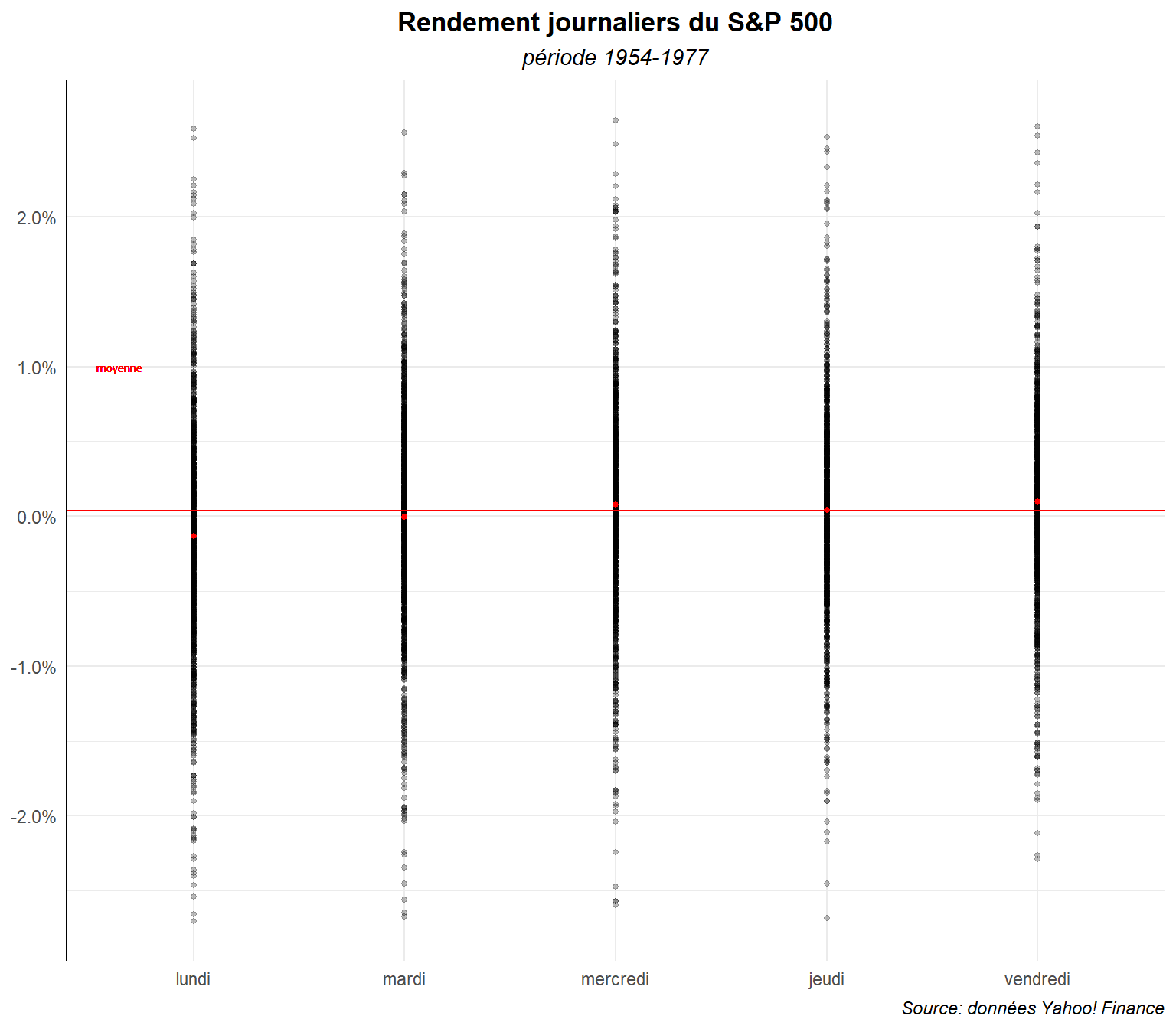
Cela améliore légèrement les choses mais au prix d’une perte d’informations.
Revenons à nos données sur l’ensemble de la période. Essayons de réduire la superposition des points en les étalant plus sur l’axe horizontale sans les faire empiéter sur ceux des jours voisins. Pour cela, à la place d’utiliser le geom_point(), utilisons le geom_jitter().
ggplot(data=dat,aes(x=day_lab,y=ret,group=day_lab))+
geom_jitter(width = 0.35,alpha=0.25,size=1) +
geom_hline(yintercept = mean(dat$ret), color='red')+
geom_text(aes(label="moyenne",x="lundi", y=0.01), color="red",
size=2,nudge_x=-0.35)+
stat_summary(fun=mean, geom="point",
size=1, color="red")+
labs(title="Rendement journaliers du S&P 500",
subtitle ="période 1954-2023",
caption="Source: données Yahoo! Finance")+
scale_y_continuous(labels = label_percent())+
theme_minimal()+
theme(
plot.title = element_text(hjust=0.5,face='bold'),
plot.subtitle = element_text(hjust=0.5,face='italic'),
plot.caption = element_text(hjust=1,face='italic'),
axis.title = element_blank(),
axis.line.y.left = element_line(color="black"),
)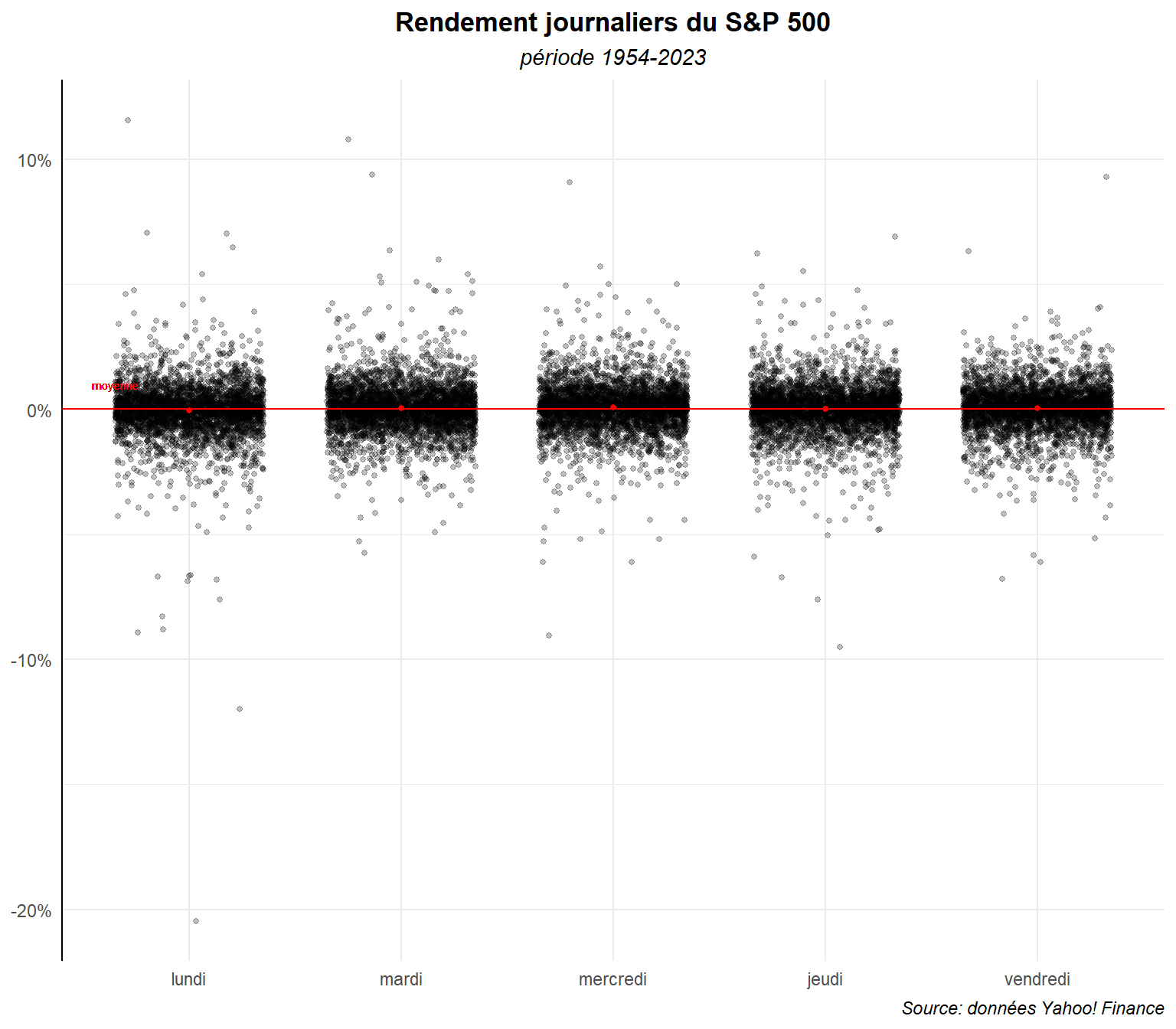
On voit plus nettement ici l’importance du nombre d’observations et des chevauchements de valeurs. L’ensemble reste néanmoins confus. On peut envisager d’ajouter des éléments d’information pour essayer de rendre les choses plus clairs comme par exemple une couleur différentes en fonction des mois où les observations sont réalisées.
ggplot(dat,
aes(y=ret,x=day_lab,color=mois_lab))+
geom_jitter(width = 0.35,alpha=0.5,size=1) +
geom_hline(yintercept=mean(dat$ret),
color='red') +
stat_summary(fun=mean, geom="point",
size=1, color="red")+
labs(title="Rendement journaliers du S&P 500",
subtitle ="période 1954-2023",
caption="Source: données Yahoo! Finance")+
scale_y_continuous(labels = label_percent())+
guides(color=guide_legend(nrow=2))+
theme_minimal()+
theme(
plot.title = element_text(hjust=0.5,face='bold'),
plot.subtitle = element_text(hjust=0.5,face='italic'),
plot.caption = element_text(hjust=1,face='italic'),
axis.title = element_blank(),
axis.line.y.left = element_line(color="black"),
legend.position = 'top',
legend.background = element_rect(color='black',
linewidth = 0.1),
legend.text = element_text(size=4),
legend.title = element_blank(),
legend.margin = margin(t=2,r=2,l=2,b=2,unit='pt'),
legend.key.size = unit(5, "pt"),
legend.byrow = TRUE
)
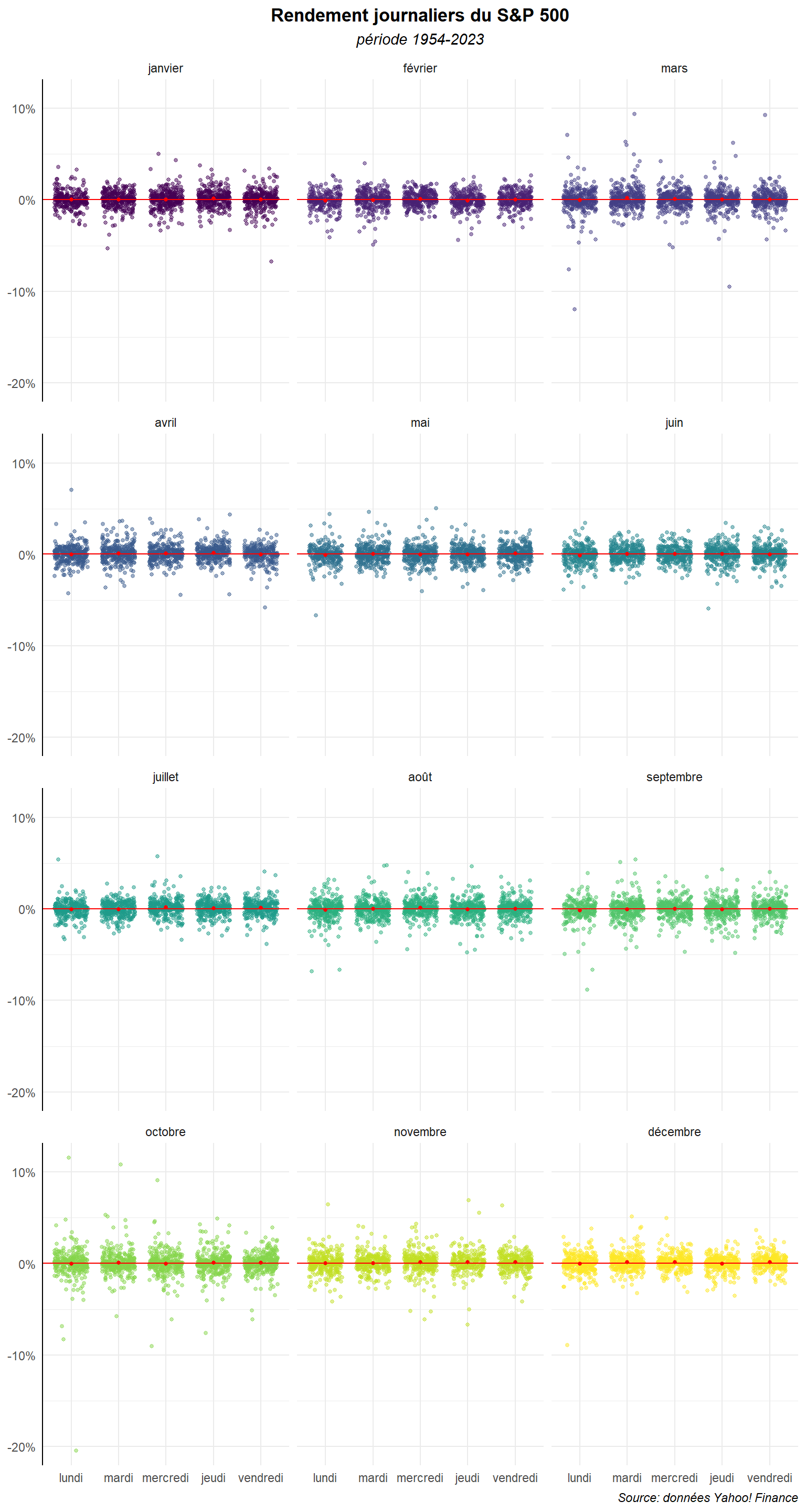
On voit encore mieux l’importance des superpositions, mais on est incapable de voir s’il y a des tendances différentes d’un mois à l’autre. Voyons ce qu’il en est, si on fait un graphe par mois à partir de la commande facet_warp().
ggplot(dat,
aes(y=ret,x=day_lab,color=mois_lab))+
geom_jitter(width = 0.35,alpha=0.5,size=1) +
geom_hline(yintercept=mean(dat$ret),
color='red') +
stat_summary(fun=mean, geom="point",
size=1, color="red")+
labs(title="Rendement journaliers du S&P 500",
subtitle ="période 1954-2023",
caption="Source: données Yahoo! Finance")+
scale_y_continuous(labels = label_percent())+
facet_wrap(~mois_lab, ncol = 3)+
theme_minimal()+
theme(
plot.title = element_text(hjust=0.5,face='bold'),
plot.subtitle = element_text(hjust=0.5,face='italic'),
plot.caption = element_text(hjust=1,face='italic'),
axis.title = element_blank(),
axis.line.y.left = element_line(color="black"),
legend.position = 'none'
)
Ajustons la taille de l’ensemble pour y voir quelque chose.
ggplot(dat,
aes(y=ret,x=day_lab,color=mois_lab))+
geom_jitter(width = 0.35,alpha=0.5,size=1) +
geom_hline(yintercept=mean(dat$ret),
color='red') +
stat_summary(fun=mean, geom="point",
size=1, color="red")+
labs(title="Rendement journaliers du S&P 500",
subtitle ="période 1954-2023",
caption="Source: données Yahoo! Finance")+
scale_y_continuous(labels = label_percent())+
facet_wrap(~mois_lab, ncol = 3)+
theme_minimal()+
theme(
plot.title = element_text(hjust=0.5,face='bold'),
plot.subtitle = element_text(hjust=0.5,face='italic'),
plot.caption = element_text(hjust=1,face='italic'),
axis.title = element_blank(),
axis.line.y.left = element_line(color="black"),
legend.position = 'none'
)
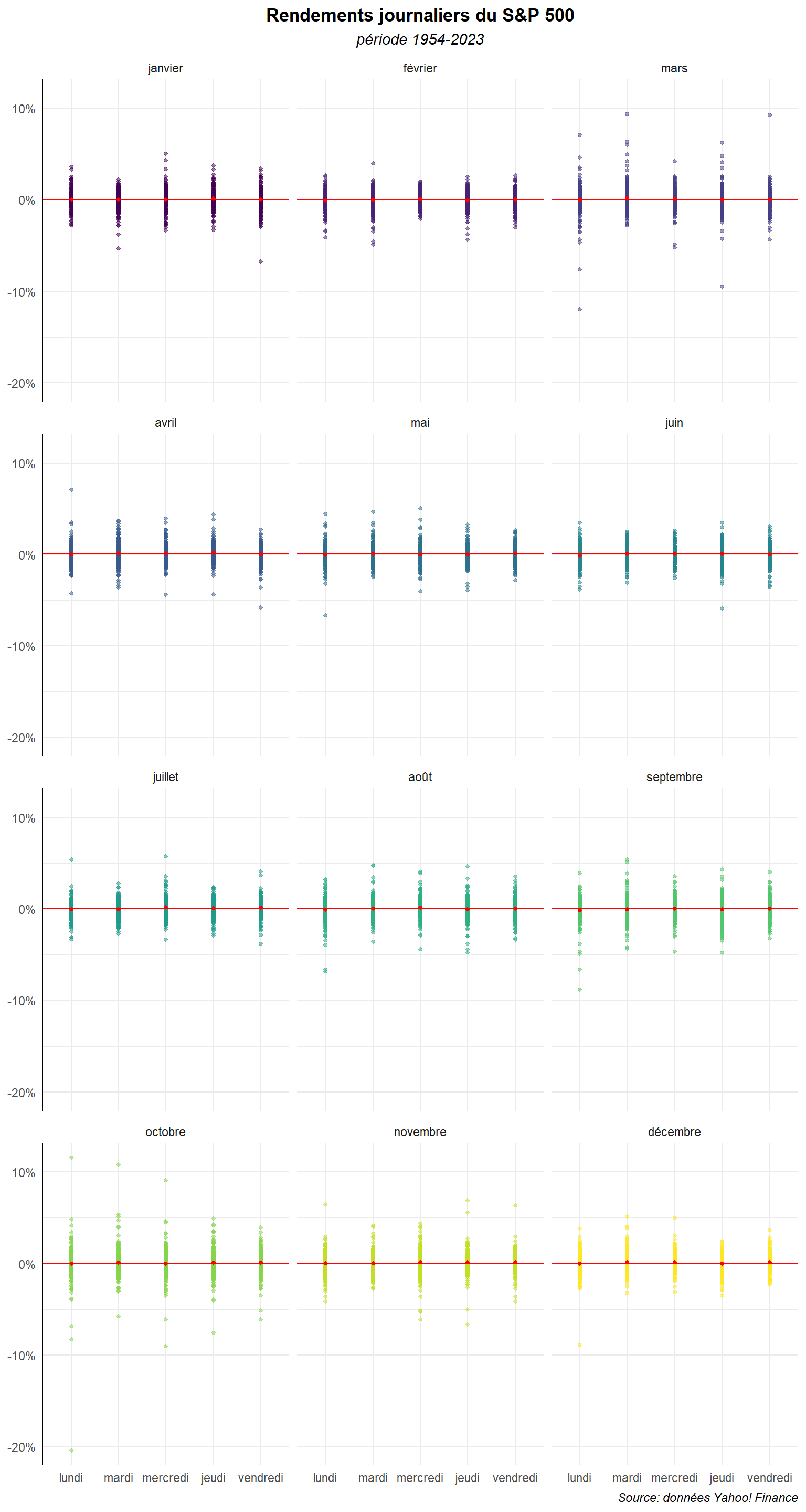
Faisons-le également pour le graphe utilisant le geom_point().
ggplot(dat,aes(y=ret,x=day_lab,color=mois_lab))+
geom_point(alpha=0.5,size=1)+
geom_hline(yintercept=mean(dat$ret),
color='red') +
stat_summary(fun=mean, geom="point",
size=1, color="red")+
labs(title="Rendements journaliers du S&P 500",
subtitle ="période 1954-2023",
caption="Source: données Yahoo! Finance")+
scale_y_continuous(labels = label_percent())+
facet_wrap(~mois_lab, ncol = 3)+
theme_minimal()+
theme(
plot.title = element_text(hjust=0.5,face='bold'),
plot.subtitle = element_text(hjust=0.5,face='italic'),
plot.caption = element_text(hjust=1,face='italic'),
axis.title = element_blank(),
axis.line.y.left = element_line(color="black"),
legend.position = 'none'
)
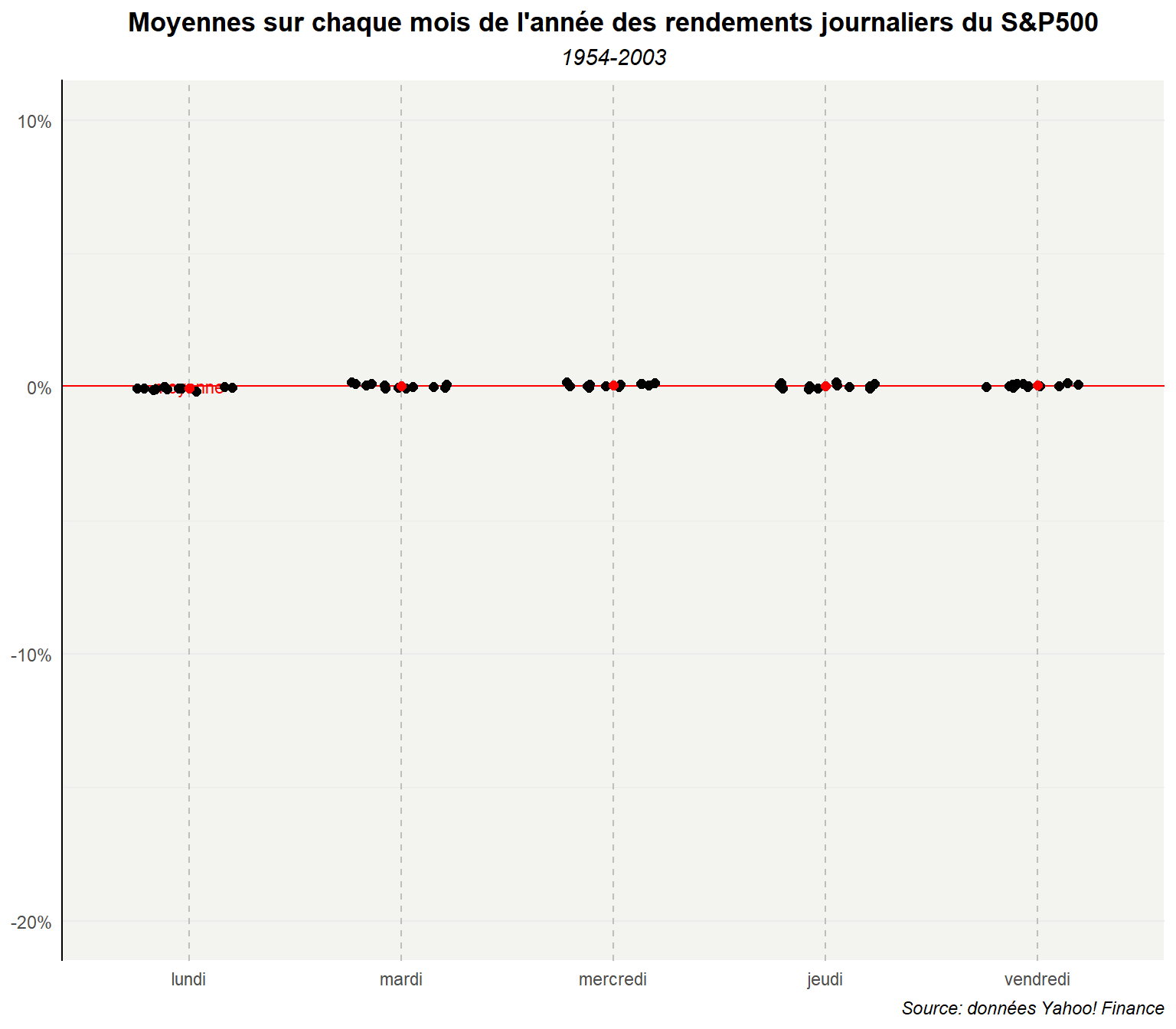
Les strip plot ne sont pas réellement adaptés à des échantillons trop gros. D’autres graphes peuvent apparaître plus pertinent. Mais, si l’on veut continuer à travailler avec ce type de représentation, on peut procéder à des regroupements de données de manières à simplifier les informations. On est alors dans une forme de bin plot. Calculons les rendements journaliers moyenne sur chaque mois (ajoutons la médiane). Marquons également les trimestres pour les utiliser plus tard pour mieux distinguer l’enchaînement des mois.
dat %>% group_by(day_lab,mois_lab) %>%
reframe(moy_md=round(mean(ret),digits=6),
med_md=round(median(ret),digits=6))->dd
dd## # A tibble: 60 × 4
## day_lab mois_lab moy_md med_md
## <ord> <ord> <dbl> <dbl>
## 1 lundi janvier 0.000105 -0.00018
## 2 lundi février -0.000878 -0.000659
## 3 lundi mars -0.000464 0
## 4 lundi avril 0.000046 0.000369
## 5 lundi mai -0.000593 -0.0005
## 6 lundi juin -0.00105 -0.000688
## 7 lundi juillet -0.00045 0
## 8 lundi août -0.000889 0.00006
## 9 lundi septembre -0.00171 -0.000716
## 10 lundi octobre -0.000243 0.000235
## # ℹ 50 more rowsÉtablissons le graphe sur cette base agrégée. On a alors 12 points par jours de la semaine, un pour chaque mois, plus la moyenne (en rouge).
ggplot(dd,aes(y=moy_md,x=day_lab))+
geom_hline(yintercept=mean(dat$ret),color='red') +
annotate(geom="text",label="moyenne",x="lundi", y=0.0005,
color="red",size=3)+
geom_jitter(width = 0.25,size=2) +
stat_summary(fun=mean, geom="point", shape=19,
size=2, color="red")+
labs(title="Moyennes sur chaque mois de l'année des rendements journaliers du S&P500",
subtitle = "1954-2003",
caption="Source: données Yahoo! Finance",
color="Mois")+
scale_y_continuous(labels = label_percent())+
scale_color_viridis_d(option="G")+
scale_shape_manual(values=c(15:17,18))+
theme_minimal()+
theme(
plot.title = element_text(hjust=0.5,face='bold'),
plot.subtitle = element_text(hjust=0.5,face='italic'),
plot.caption = element_text(hjust=1,face='italic'),
axis.title = element_blank(),
axis.line.y.left = element_line(color="black"),
panel.grid.major.x = element_line(linetype = "dashed",
colour = "gray"),
panel.background = element_rect(fill='#F3F3EF',colour = 'white'),
panel.border = element_blank(),
legend.position = 'none'
)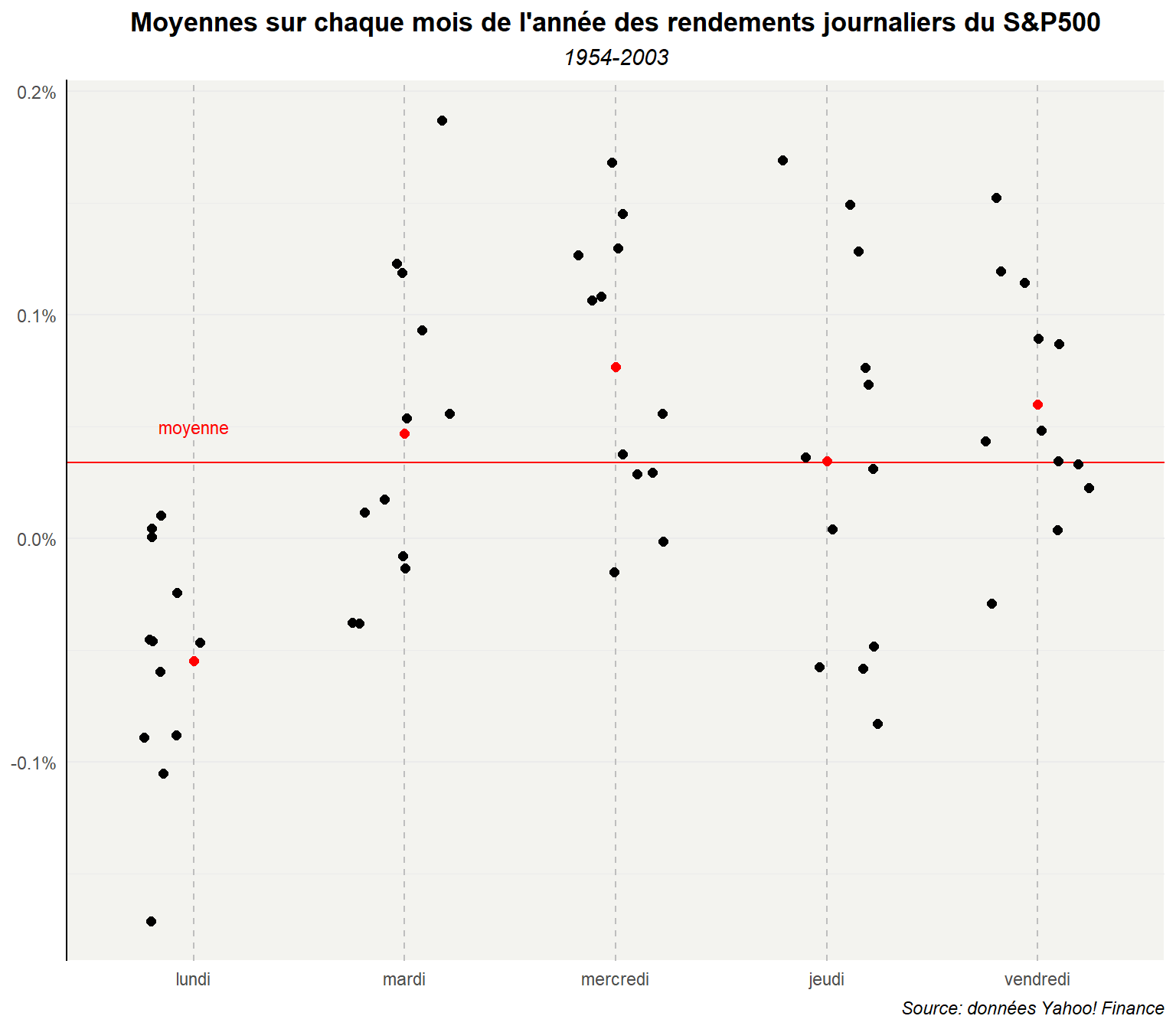
L’effet lundi semble ici plus marqué. Néanmoins, il faut se méfier d’une part parce que la moyennisation réduit l’étendu de valeur et d’autre part qu’il faut éviter d’interpréter les corrélations relevées sur les moyennes sur une base désagrégée. Il y a un risque d’erreur écologique (ecological fallacy). Il ne faut pas faire d’inférences abusives. Certaines structures dans les données individuelles peuvent être distordues pour la moyennisation autour de groupe désignée arbitrairement. Par ailleurs, au sein de ces groupes la distribution des valeurs peut être asymétrique et dans ces conditions on peut difficilement dire que les tendances constatées sur la base des moyennes reflètent parfaitement ce que l’observerait pour des unités tirées au hasard dans les différents groupes d’agrégation.
Pour illustrer le premier point, reprenons le graphe et étendons les plages de valeurs pour avoir les mêmes que dans le cas non agrégé.
ggplot(dd,aes(y=moy_md,x=day_lab))+
geom_hline(yintercept=mean(dat$ret),color='red') +
annotate(geom="text",label="moyenne",x="lundi", y=0.0005,
color="red",size=3)+
geom_jitter(width = 0.25,size=2) +
stat_summary(fun=mean, geom="point", shape=19,
size=2, color="red")+
labs(title="Moyennes sur chaque mois de l'année des rendements journaliers du S&P500",
subtitle = "1954-2003",
caption="Source: données Yahoo! Finance",
color="Mois")+
scale_y_continuous(labels = label_percent())+
scale_color_viridis_d(option="G")+
scale_shape_manual(values=c(15:17,18))+
coord_cartesian(ylim=c(-0.2,0.1))+
theme_minimal()+
theme(
plot.title = element_text(hjust=0.5,face='bold'),
plot.subtitle = element_text(hjust=0.5,face='italic'),
plot.caption = element_text(hjust=1,face='italic'),
axis.title = element_blank(),
axis.line.y.left = element_line(color="black"),
panel.grid.major.x = element_line(linetype = "dashed",
colour = "gray"),
panel.background = element_rect(fill='#F3F3EF',colour = 'white'),
panel.border = element_blank(),
legend.position = 'none'
)
Pour illustrer le second point, réalisons le graphe à partir des médianes.
ggplot(dd,aes(y=med_md,x=day_lab))+
geom_hline(yintercept=median(dat$ret),color='red') +
annotate(geom="text",label="médiane",x="lundi", y=0.0005,
color="red",size=3)+
geom_jitter(width = 0.25,size=2) +
stat_summary(fun=mean, geom="point", shape=19,
size=2, color="red")+
labs(title="Médiane sur chaque mois de l'année des rendements journaliers du S&P500",
subtitle = "1954-2003",
caption="Source: données Yahoo! Finance",
color="Mois")+
scale_y_continuous(labels = label_percent())+
scale_color_viridis_d(option="G")+
scale_shape_manual(values=c(15:17,18))+
theme_minimal()+
theme(
plot.title = element_text(hjust=0.5,face='bold'),
plot.subtitle = element_text(hjust=0.5,face='italic'),
plot.caption = element_text(hjust=1,face='italic'),
axis.title = element_blank(),
axis.line.y.left = element_line(color="black"),
panel.grid.major.x = element_line(linetype = "dashed",
colour = "gray"),
panel.background = element_rect(fill='#F3F3EF',colour = 'white'),
panel.border = element_blank(),
legend.position = 'none'
)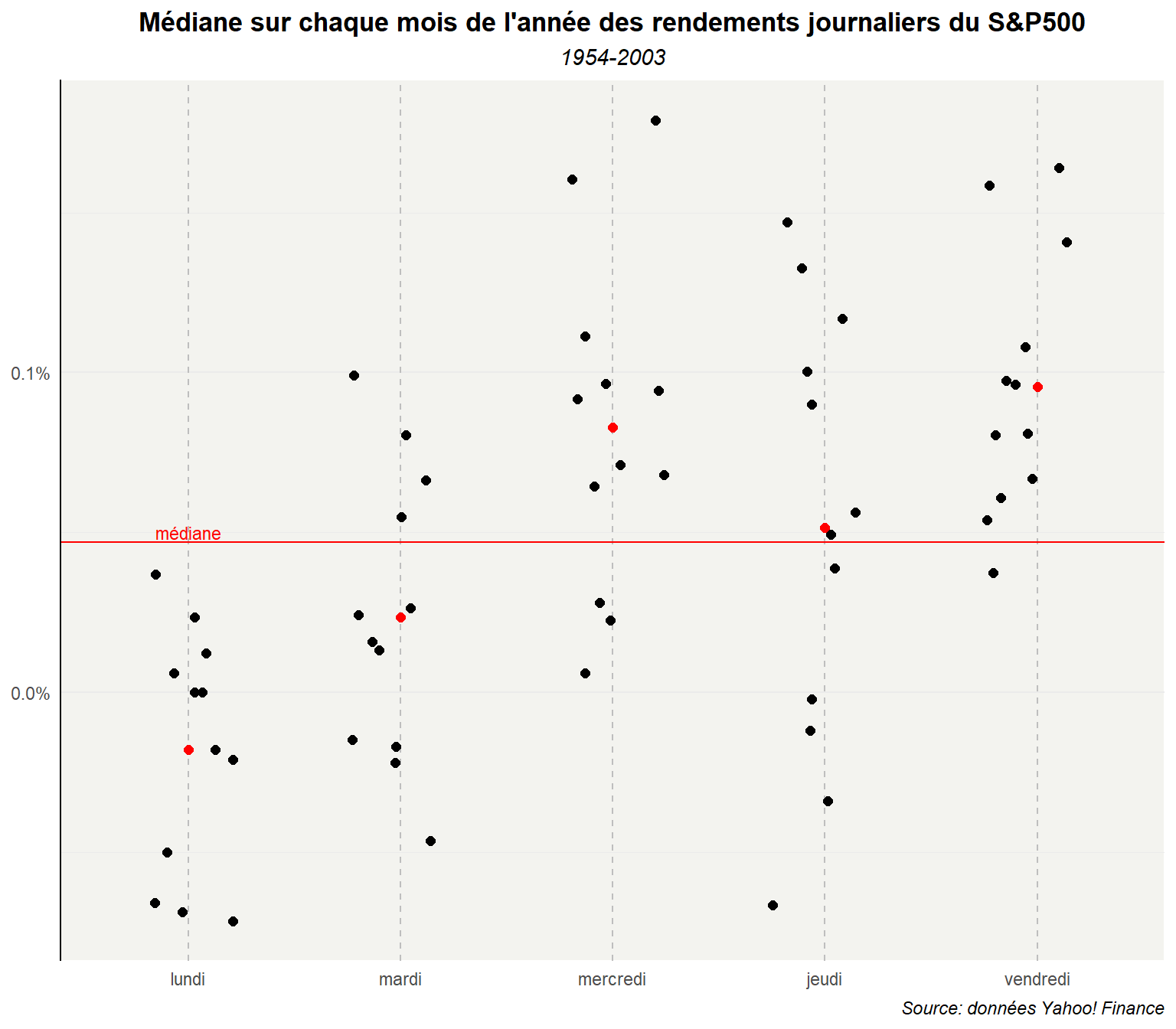
La médiane donne moins de poids aux valeurs extrêmes. Il en résulte des points plus proches les uns des autres.
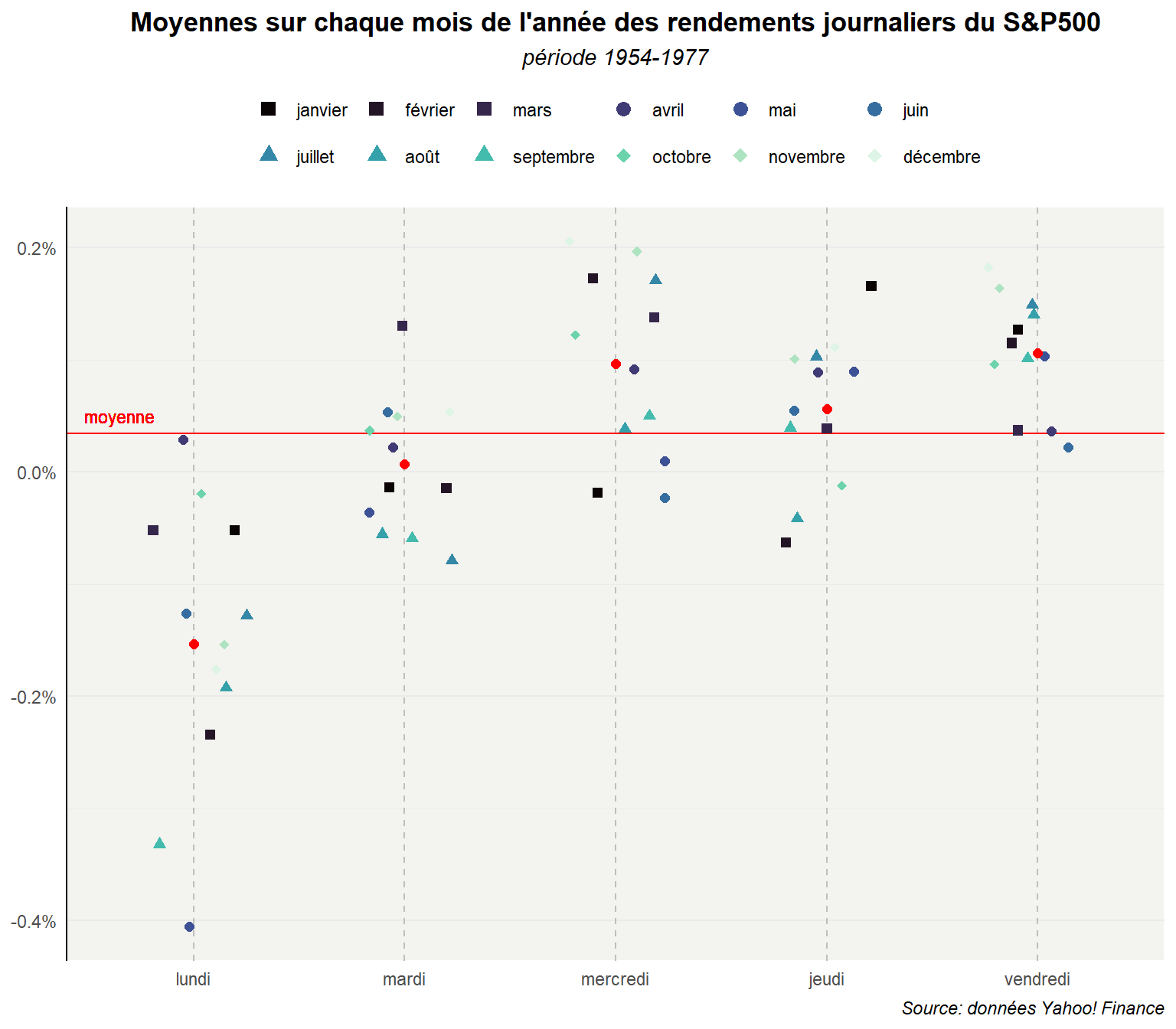
On peut réaliser le graphe pour la période 1954-77 et ajouter des informations complémentaires comme de la couleur pour distinguer les mois et des formes pour les trimestres. Revenons sur la configuration avec les moyennes. Commençons par préparer les données.
dat %>% filter(date>date("1953/01/01")&
date<date("1977/12/31")) %>%
group_by(day_lab,mois_lab) %>%
reframe(moy_md=round(mean(ret),digits=6),
trim=unique(trimestre))->dd_54_77
dd_54_77## # A tibble: 60 × 4
## day_lab mois_lab moy_md trim
## <ord> <ord> <dbl> <int>
## 1 lundi janvier -0.000522 1
## 2 lundi février -0.00235 1
## 3 lundi mars -0.000523 1
## 4 lundi avril 0.000291 2
## 5 lundi mai -0.00406 2
## 6 lundi juin -0.00126 2
## 7 lundi juillet -0.00128 3
## 8 lundi août -0.00192 3
## 9 lundi septembre -0.00332 3
## 10 lundi octobre -0.000195 4
## # ℹ 50 more rowsLe graphe reprend alors les mêmes commandes.
ggplot(dd_54_77,
aes(y=moy_md,x=day_lab,color=mois_lab,
shape=factor(trim)))+
geom_hline(yintercept=mean(dat$ret),
color='red') +
geom_text(aes(label="moyenne",x="lundi", y=0.0005), color="red",
size=3,nudge_x=-0.35)+
geom_jitter(width = 0.25,size=2) +
stat_summary(fun=mean, geom="point", shape=19,
size=2, color="red")+
labs(title="Moyennes sur chaque mois de l'année des rendements journaliers du S&P500",
subtitle ="période 1954-1977",
caption="Source: données Yahoo! Finance",
color="Mois")+
scale_y_continuous(labels = label_percent())+
scale_color_viridis_d(option="G")+
scale_shape_manual(values=c(15:18))+
guides(
shape="none",
color = guide_legend(override.aes = list(size = 3,
shape=c(15,15,15,
16,16,16,
17,17,17,
18,18,18)),
nrow=2))+
theme_minimal()+
theme(
plot.title = element_text(hjust=0.5,face='bold'),
plot.subtitle = element_text(hjust=0.5,face='italic'),
plot.caption = element_text(hjust=1,face='italic'),
axis.title = element_blank(),
axis.line.y.left = element_line(color="black"),
panel.grid.major.x = element_line(linetype = "dashed",
colour = "gray"),
panel.background = element_rect(fill='#F3F3EF',colour = 'white'),
panel.border = element_blank(),
legend.position = 'top',
legend.title = element_blank(),
legend.byrow = TRUE
)
Comme vous le voyez les possibilités sont multiples que l’on travail avec des données individuelles ou des données agrégées même si dans ce cas il faudra être précautionneux sur l’interprétation. Lorsque comme ici l’on a un grand nombre d’observations données le strip plot n’est pas toujours le plus adapté. Dans les prochains postes nous verrons des modes de représentations plus performants.