Dans cet avant dernier post consacré à la représentation des séries temporelles, nous revenons sur la question de l’évolution du lien entre deux variables dans le temps. Nous l’avions déjà aborder lorsque nous avions traité des graphes à doubles ordonnées (dual axis plot). J’avais alors émis certaines réserves concernant cette représentation, qui peut donner l’illusion d’une corrélation voir d’une causalité. J’avais alors indiqué ma préférence pour les nuages de points quitte à marquer le temps à l’aide d’une progression de couleurs. Ici, la démarche est proche si ce n’est que le temps est marqué par une série d’étiquettes attachées aux différents points.
Pour illustrer sa construction et la lecture que l’on peut en faire, considérons l’évolution conjointe PIB per capita (par habitant) aux Etats-Unis et du prix du mètre cube de pétrole sur la période 1964-2018. Nous tirons les données, comme souvent, du site Ourworldindata.org. Nous y reviendrons. Mais, avant d’aller plus loin, chargeons les packages mobilisés par la suite. Nous y incluons, comme toujours, le très classique tidyverse mais aussi scales, qui nous servira à mettre en forme les axes du repaire, et ggrepel, qui permet de placer des étiquettes.
library(tidyverse)
library(scales)
library(ggrepel)Ceci fait, chargeons les données. Commençons par les prix du pétrole. La série est obtenue à partir de la page dédiée du site ourworldindata. Vous pouvez également la trouver ici. Stockons-la dans une dataframe nommée oil et profitons-en pour pratiquer quelques mises en forme (changement de nom de variables, limitations). Visualisons le résultat.
oil<- read_csv("crude-oil-prices.csv") %>%
rename(Oil=`Oil price - Crude prices since 1861 (current US$)`) %>%
select(Year,Oil) %>%
filter(Year>=1964&Year<=2018)
glimpse(oil)## Rows: 55
## Columns: 2
## $ Year <dbl> 1964, 1965, 1966, 1967, 1968, 1969, 1970, 1971, 1972, 1973, 1974,…
## $ Oil <dbl> 11.32164, 11.32164, 11.32164, 11.32164, 11.32164, 11.32164, 11.32…Chargeons également le PIB per capita. On le trouve également dans ourworldindata ou l’obtenir à partir de ce lien ici. Nommons-la dataframe obtenue gdp. Profitons-en pour limiter la base aux seuls Etats-Unis, aux variables d’intérêt et à la période 1964-2018. Renommons la variable “GDP per capita” pour en avoir une version plus simple à manipuler.
gdp<- read_csv("gdp-per-capita-maddison.csv") %>%
filter(Entity=='United States') %>%
select(-Entity,-Code,-`417485-annotations`) %>%
rename(PIB="GDP per capita") %>%
filter(Year>=1964&Year<=2018)
glimpse(gdp)## Rows: 55
## Columns: 2
## $ Year <dbl> 1964, 1965, 1966, 1967, 1968, 1969, 1970, 1971, 1972, 1973, 1974,…
## $ PIB <dbl> 20360, 21390, 22529, 22842, 23691, 24195, 23958, 24394, 25414, 26…Réunissons les deux dataframe dans une seule. Utilisons l’année Year comme clé de croisement.
dat<-left_join(gdp,oil,by = join_by(Year))
glimpse(dat)## Rows: 55
## Columns: 3
## $ Year <dbl> 1964, 1965, 1966, 1967, 1968, 1969, 1970, 1971, 1972, 1973, 1974,…
## $ PIB <dbl> 20360, 21390, 22529, 22842, 23691, 24195, 23958, 24394, 25414, 26…
## $ Oil <dbl> 11.32164, 11.32164, 11.32164, 11.32164, 11.32164, 11.32164, 11.32…Maintenant que nous avons les données, voyons ce que donne les séries une à une. Commençons par établir une courbe de l’évolution du PIB. Mettons-la directement en forme.
ggplot(data=dat,aes(x=Year,PIB))+
geom_line(color='blue')+
labs(title="Evolution du PIB per capita",
subtitle = "(aux Etats-Unis sur la période 1964-2018)",
caption = "Source: OurWorldinData.com")+
scale_x_continuous(breaks=seq(1965,2020,5))+
scale_y_continuous(breaks=seq(20000,55000,5000),labels = label_dollar())+
coord_cartesian(xlim=c(1963,2019),ylim=c(20500,57000),expand = FALSE)+
theme_minimal()+
theme(
plot.title = element_text(hjust = 0.5,face='bold'),
plot.subtitle = element_text(hjust = 0.5,face='italic'),
plot.caption = element_text(hjust = 1, face='italic'),
axis.title = element_blank(),
axis.line = element_line(),
axis.ticks = element_line(),
panel.grid.minor = element_blank()
)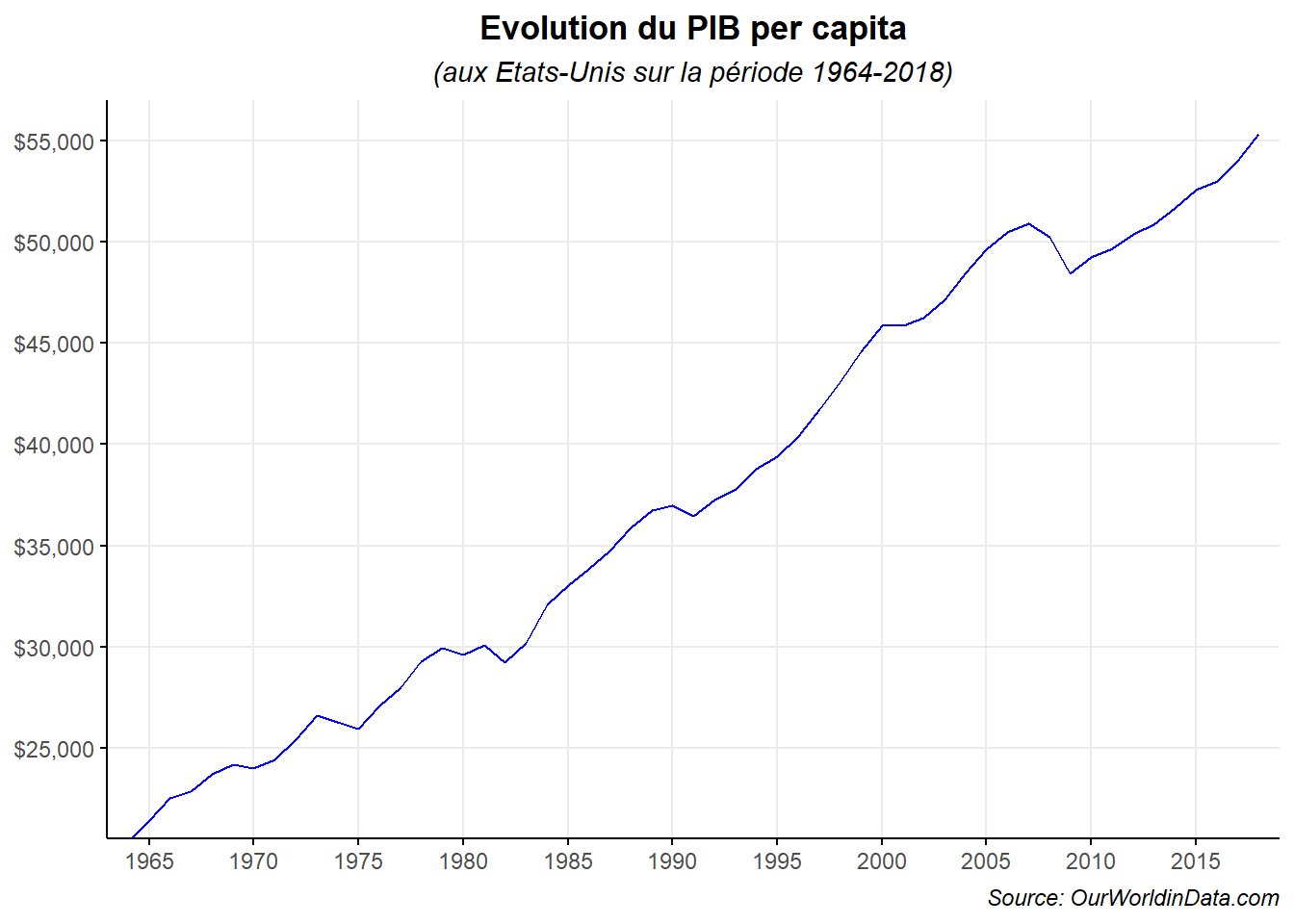
On constate une hausse nette du PIB per capital entre 1964 et 2018 avec des périodes d’accélération et de ralentissement. Voyons sur le même modèle le prix du métre cube de pétrole.
ggplot(data=dat,aes(x=Year,Oil))+
geom_line(color='blue')+
labs(title="Evolution du prix du métre cube de pétrole",
subtitle = "(sur la période 1964-2018)",
caption = "Source: OurWorldinData.com")+
scale_x_continuous(breaks=seq(1965,2020,5))+
scale_y_continuous(breaks=seq(0,800,200),label=label_dollar())+
coord_cartesian(xlim=c(1963,2019),ylim=c(0,800),expand = FALSE)+
theme_minimal()+
theme(
plot.title = element_text(hjust = 0.5,face='bold'),
plot.subtitle = element_text(hjust = 0.5,face='italic'),
plot.caption = element_text(hjust = 1, face='italic'),
axis.title = element_blank(),
axis.line = element_line(),
axis.ticks = element_line(),
panel.grid.minor = element_blank()
)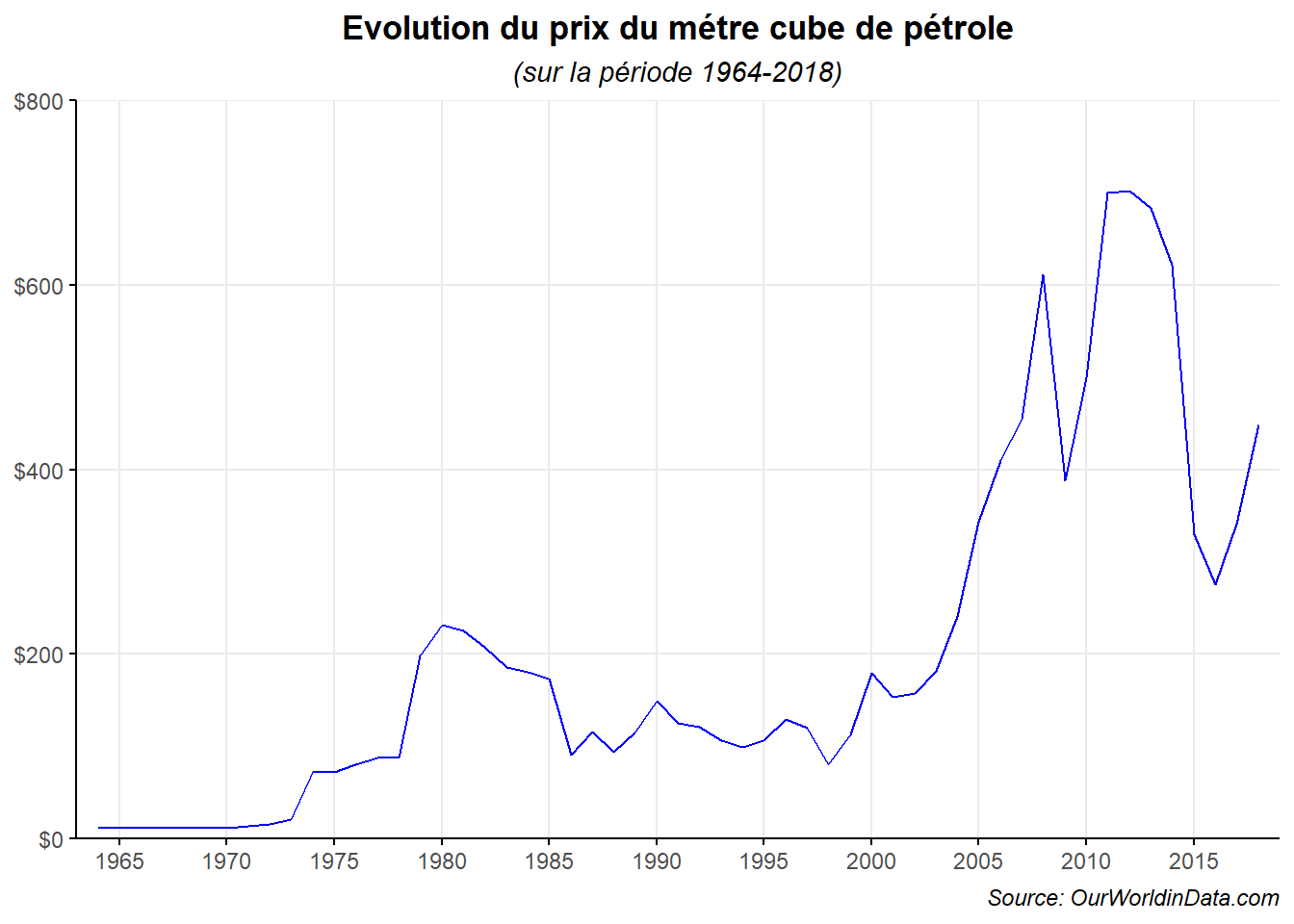
On a également une série croissante sur la période mais cette fois celle-ci est plus heurté avec de claires phases intermédiaires de décroissance, de stagnation et de croissance.
Avant plus réalisons quelques tests statistiques.Prenons l’ensemble de la période.
round(c(cor.test(dat$PIB,dat$Oil)$estimate,
cor.test(dat$PIB,dat$Oil)$statistic,
p_value=cor.test(dat$PIB,dat$Oil)$p.value),digits=3)## cor t p_value
## 0.763 8.580 0.000On a bien une corrélation forte entre le PIB et le prix du pétrole si on considère l’ensemble de la période. Mais qu’en est-il si l’on s’intéresse au sous période. Prenons par exemple la sous-période 1986-2000 sur laquelle le prix du pétrole varie relativement peu. 7
dat_1986_2000<-filter(dat,Year>=1986&Year<=2000)
round(c(cor.test(dat_1986_2000$PIB,dat_1986_2000$Oil)$estimate,
cor.test(dat_1986_2000$PIB,dat_1986_2000$Oil)$statistic,
p_value=cor.test(dat_1986_2000$PIB,dat_1986_2000$Oil)$p.value),digits=3)## cor t p_value
## 0.341 1.307 0.214Sur la sous période, la corrélation des séries n’est pas statistiquement significative.
Le nuage de points connectés permet de mettre en évidence ce type de tendance.Pour cela, nous utilisons geom_point(), geom_segment() et geom_text_repel(). Le premier marque d’un point l’intersection des valeurs du PIB et du prix du pétrole pour chaque observation (année). Le second permet de relier ces points.Pour cela, nous utilisons la fonction lead() pour désigner les points d’arrivé des segments (end). Le troisième positionne les étiquette indiquant l’année de manière à la rendre lisible. Concernant la mise en forme gardons la même que celle utilisée pour les courbes de série temporelle classique.
ggplot(data=dat,aes(x = PIB,y = Oil))+
geom_point()+
geom_segment(color="#69b3a2",
aes(xend=lead(PIB),yend=lead(Oil)))+
geom_text_repel(aes(label=as.character(Year)))+
labs(title="Evolution du PIB per capita aux Etats-Unis et du prix du métre cube de pétrole",
subtitle = "(sur la période 1964-2018)",
caption = "Source: OurWorldinData.com")+
scale_x_continuous(breaks=seq(20000,55000,5000),labels = label_dollar())+
scale_y_continuous(breaks=seq(0,800,200),label=label_dollar())+
theme_minimal()+
theme(
plot.title = element_text(hjust = 0.5,face='bold'),
plot.subtitle = element_text(hjust = 0.5,face='italic'),
plot.caption = element_text(hjust = 1, face='italic'),
axis.title = element_blank(),
axis.line = element_line(),
axis.ticks = element_line(),
panel.grid.minor = element_blank())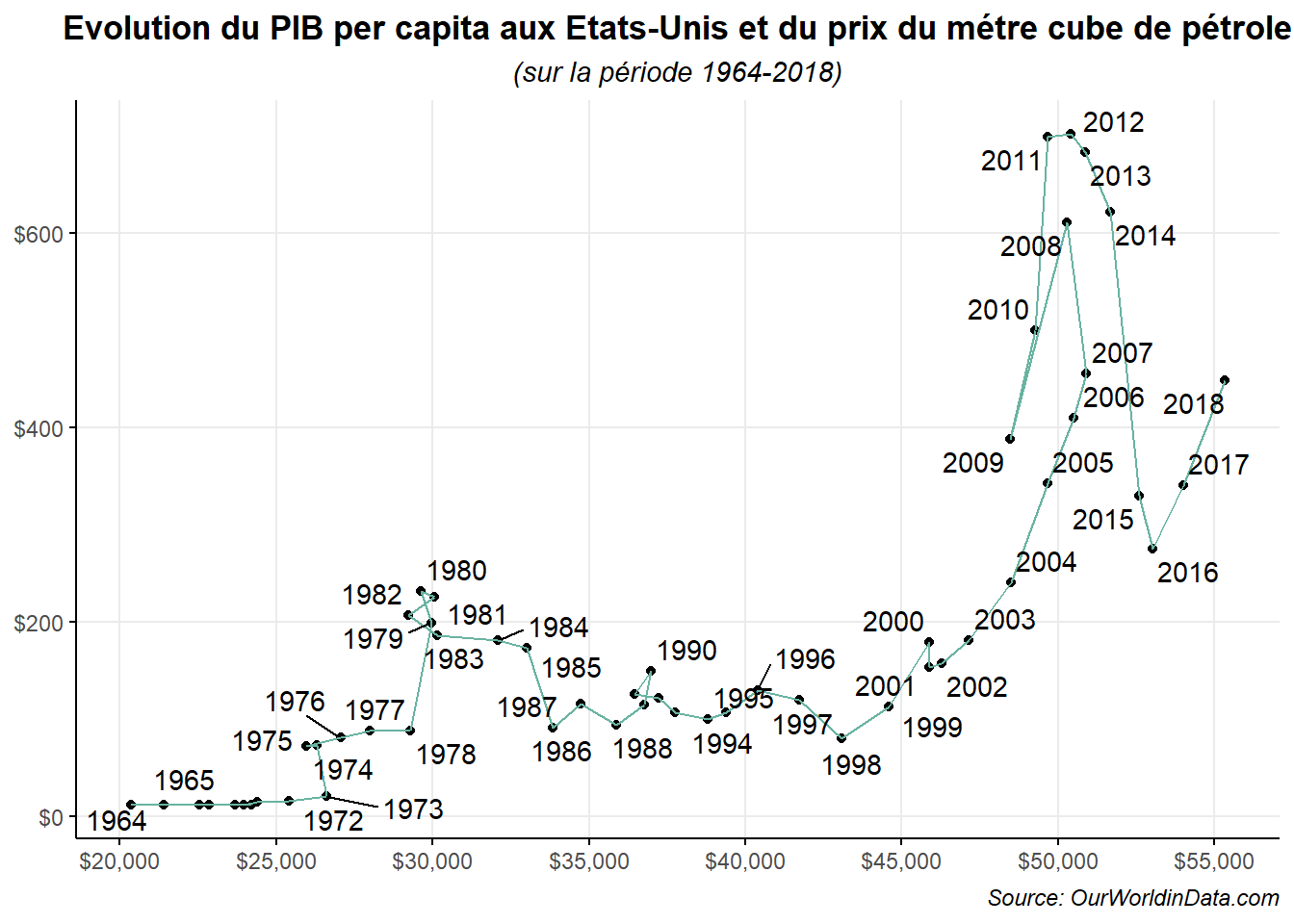
On voit nettement que sur le début de la période entre 1964 et 1973, le prix du pétrole ne varie pas alors que le PIB augmente. On a donc une absence de corrélation. Puis, une augmentation du prix en 1974 est associé avec un léger recul du PIB. Ensuite, le prix stagne à nouveau jusqu’en 1978 tandis que le PIB augmente. En fait, on voit clairement que la période pour laquelle la corrélation positive entre les deux séries est la plus nette est celle courant entre 1998 et 2007.
Il serait possible d’aller plus loin dans le commentaire du graphe en détaillant les phases d’association ou de dissociation et les chocs conduisant à des changements. Mais, nous laissons au lecteur le loisir de le faire pour prendre conscience des possibilités de ce type de représentation en termes de mises au jours des complexités des phénomènes temporels étudiés.