Pour ce dernier poste de la série, l’idée est d’abordé rapidement les traitements de variables continuent qui s’éloignent d’une loi normale. Nous traiterons rapidement de la transformation logarithmique et la winsorisation. L’exemple pris n’est pas le plus pertinent (deux des trois variables suivent vraisemblablement des lois normales), mais les étudiants ont déjà utilisé ces données. J’en profites pour montrer comment on crée des fonctions permettant d’aller plus vite dans les traitements avec la création d’histogrammes et de tableaux de présentation des résultats de régression.
Comme à chaque fois, commençons par charger les packages que nous allons utiliser.
library(tidyverse)
library(scales)
library(patchwork)
library(haven)
library(moments)
library(lmtest)
library(sandwich)
library(broom)
library(DescTools)
library(gt)Chargeons les données sur lesquelles nous allons travailler. Utilisons une nouvelle fois l’étude sur les écoles californiennes.
dat<-read_dta("caschool.dta")Limitons notre attention sur l’explication des résultats au teste des niveau (testscr) par le nombre d’élèves par professeur (str) et le pourcentage d’élèves dont l’anglais n’est pas la langue natale (el_pct). Mais avant d’aller plus loin, voyons quelques statistiques descriptives.
| Average | Std. Dev. | Skewness | Kurtosis | Percentiles | |||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 10% | 25% | 40% | 50% | 60% | 75% | 90% | |||||
| score | 654.16 | 19.05 | 0.09 | 2.75 | 630.40 | 640.05 | 649.07 | 654.45 | 659.40 | 666.66 | 678.86 |
| taux d'encadrement | 19.64 | 1.89 | -0.03 | 3.61 | 17.35 | 18.58 | 19.27 | 19.72 | 20.08 | 20.87 | 21.87 |
| % de non angl | 15.77 | 18.29 | 1.43 | 4.44 | 0.00 | 1.94 | 5.01 | 8.78 | 13.14 | 22.97 | 43.78 |
La Kurtosis d’une distribution normale est 3. Au dessus de 3, la distribution est moins aplatie qu’une loi normale. En dessous de 3, la distribution est plus aplatie. La Skewness d’une distribution normale est 0. Au dessus de 0, la distribution est asymétrique sur la gauche. En dessous de 0, la distribution est asymétrique sur la droite.
Ici, on voit que l’on est pas très éloignés de la loi normale concernant la Kurtosis et la Skewness pour les testes de niveau (testscr) et le taux d’encadrement (str), mais que ce n’est pas le cas pour le pourcentage d’élève dont l’anglais n’est pas la première langue (el_pct).
Observons cela au travers d’histogrammes sur lesquels les lois normales correspondant aux données sont projetées. Pour éviter des réplication de codes trop long par la suite, créons une fonction.
hist_dist_<-function(var1,df,nom){
attach(df)
x<-var1
detach()
ggplot(data = df,aes(x=x))+
geom_histogram(aes(y =after_stat(density)),bins=30,
fill='grey',color='black')+
geom_vline(xintercept = mean(x) ,color='red')+
stat_function(fun = dnorm,
args = list(mean = mean(x), sd = sd(x)))+
labs(x=nom)+
#scale_y_continuous(labels = label_percent())+
theme_minimal()}Ceci fait, présentons les graphes de nos trois variables.
G1<-hist_dist_(var1 = testscr,df=dat,nom="score")
G2<-hist_dist_(var1 = str,df=dat,nom="taux d'encadrement")
G3<-hist_dist_(var1 = el_pct,df=dat,nom="% de non angl")
G1/(G2+G3)
Évaluons le modèle linéaire expliquant les résultats du teste par le taux d’encadrement et le pourcentage de non anglophone. Utilisons une estimation robuste à l’hétéroscédasticité des tests sur les coefficients.
Comme nous allons estimé plusieurs fois le modèle est qu’à chaque fois nous souhaitons avoir un tableau de résultat élégant, créons comme une fonction permettant de les répliquer plus facilement.
reg_<-function(model,don,lab,opt="lign"){
reg<-lm(model,data=don)
reg_t<-tidy(coeftest(reg,vcov=vcovHC(reg,'HC0'))) %>%
mutate(term=c(lab),
estimate=round(estimate,digits=3),
std.error=round(std.error,digits=3),
statistic=round(statistic,digits=3),
p.value=round(p.value,digits=3),
star=ifelse(p.value<=0.01,'***',
ifelse(p.value>0.01|p.value<=0.05,'**',
ifelse(p.value>0.05|p.value<=0.1,'*',' '))))
gl<-glance(reg)
qa<-round(gl$adj.r.squared,digits=4)
fish<-round(gl$statistic,digits=2)
df<-gl$nobs
eto<-ifelse(gl$p.value<=0.01,'***',
ifelse(gl$p.value>0.01|gl$p.value<=0.05,'**',
ifelse(gl$p.value>0.05|gl$p.value<=0.1,'*',' ')))
if (opt=="lign") {
R2<-c('Adj_R2',qa,'','','','')
fisher<-c('F de fisher',fish,eto,'','','')
nb<-c('nobs',df,'','','','')
reg_t<-rbind(reg_t,R2,fisher,nb)
return(reg_t)}
if (opt=="col_sd"){
ff<-c();mod<-c();st<-c()
for (i in 1:length(lab)){
f<-rbind(reg_t[i,1],'')
g<-rbind(reg_t$estimate[i],
paste('(',reg_t$std.error[i],')'))
s<-rbind(reg_t$star[i],'')
ff<-rbind(ff,f)
mod<-rbind(mod,g)
st<-rbind(st,s)}
tb<-tibble(ff,mod,' '=st)
R2<-c('Adj_R2',qa,'')
fisher<-c('F de fisher',fish,eto)
nb<-c('nobs',df,'')
tb<-rbind(tb,R2,fisher,nb)}
return(tb)}La fonction prévoit deux types de sortie que l’on peut appeler par l’option opt. La première ‘lign’, qui est celle donné par défaut, présente les coefficient, l’erreur standard, les t stat, les p-value et les étoiles d’interprétation.
r1<-reg_(testscr~str+el_pct,don=dat,
lab=c('constante',"taux d'encadrement",'% de non angl'))Créons une fonction pour la mise en forme de ce type de tableau à partir du package gt.
mis_lign<-function(t){
gt(t) %>%
tab_style(style=list(cell_fill(color = "#F9E3D6"),
cell_text(style = "italic")),
locations = cells_body(columns = c(2:6),
rows=c(1:3)))%>%
tab_style(style = cell_borders(sides = "bottom",color = "black",
weight = px(2),style = "solid"),
locations = cells_body(columns = everything(),
rows = c(3,6)))}Voyons ce que cela donne.
mis_lign(r1)| term | estimate | std.error | statistic | p.value | star |
|---|---|---|---|---|---|
| constante | 686.032 | 8.697 | 78.882 | 0 | *** |
| taux d'encadrement | -1.101 | 0.431 | -2.553 | 0.011 | ** |
| % de non angl | -0.65 | 0.031 | -21.014 | 0 | *** |
| Adj_R2 | 0.4237 | ||||
| F de fisher | 155.01 | *** | |||
| nobs | 420 |
La second option ‘col_sd’ présente les résultats en colonnes mais en se limitant pour les testes à fournir l’erreur-standard entre parenthèses sous le coefficient.
reg_base<-reg_(testscr~str+el_pct,don=dat,opt='col_sd',
lab=c('constante',"taux d'encadrement",
'% de non angl'))
reg_base## # A tibble: 9 × 3
## term mod[,1] ` `[,1]
## <chr> <chr> <chr>
## 1 "constante" 686.032 "***"
## 2 "" ( 8.697 ) ""
## 3 "taux d'encadrement" -1.101 "**"
## 4 "" ( 0.431 ) ""
## 5 "% de non angl" -0.65 "***"
## 6 "" ( 0.031 ) ""
## 7 "Adj_R2" 0.4237 ""
## 8 "F de fisher" 155.01 "***"
## 9 "nobs" 420 ""Procédons de la même manière que précédemment en créant une fonction de mise en forme.
mis_col_sd<-function(t){
gt(t) %>%
tab_style(style=list(cell_fill(color = "#F9E3D6"),
cell_text(style = "italic")),
locations = cells_body(columns = c(2:length(t)),
rows=c(1:6)))%>%
tab_style(style = cell_borders(sides = "bottom",color = "black",
weight = px(2),style = "solid"),
locations = cells_body(columns = everything(),
rows = c(6,9)))}Voyons ce que cela donne.
mis_col_sd(reg_base)| term | mod | |
|---|---|---|
| constante | 686.032 | *** |
| ( 8.697 ) | ||
| taux d'encadrement | -1.101 | ** |
| ( 0.431 ) | ||
| % de non angl | -0.65 | *** |
| ( 0.031 ) | ||
| Adj_R2 | 0.4237 | |
| F de fisher | 155.01 | *** |
| nobs | 420 |
Au delà des questions de mise en forme, on retrouve bien les résultats déjà mis en évidence dans le post TQG 4 (tâche 2). Si on examine les résidus de la régression, on est proche de la loi normale.
hist_dist_(var1 = lm(testscr~str+el_pct,data=dat)$residu,
df=dat,nom="residus")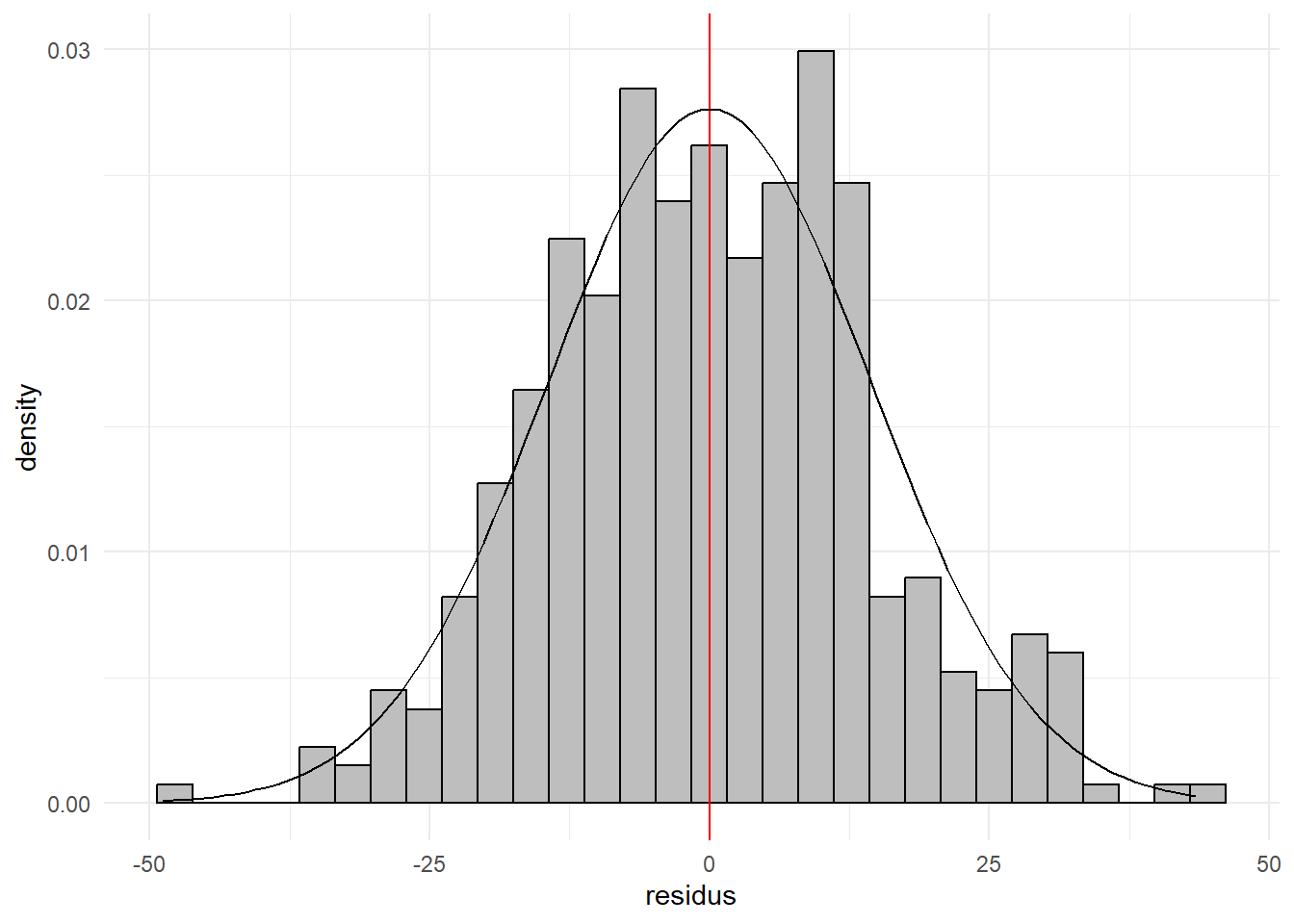
Cela se voit aussi bien graphiquement que sur la base des skewness et kurtosis.
c(sk=skewness(lm(testscr~str+el_pct,data=dat)$residu),
kurt=kurtosis(lm(testscr~str+el_pct,data=dat)$residu))## sk kurt
## 0.08779899 3.02389815le passage par le log
Une des façons de linéariser les relations mises en évidence dans une régression est de passer l’ensemble par le logarithme en veillant à éviter les cas de log(0). Le passage au log rapproche la distribution de la variable de celle d’une loi normale (log normale).
Procédons à la transformation sur nos variables.
dat_log<-dat %>% mutate(
testscr=log(testscr+1),str=log(str+1),el_pct=log(el_pct+1))Observons ses conséquences à partir des histogrammes des variables nouvelles versions.
G1<-hist_dist_(var1 = testscr,df=dat_log,nom="score")
G2<-hist_dist_(var1 = str,df=dat_log,nom="taux d'encadrement")
G3<-hist_dist_(var1 = el_pct,df=dat_log,nom="% de non angl")
G1/(G2+G3)
Si ce n’est les échelles, peu de choses ont changé concernant nos deux premières variables. Par contre, on voit clairement un changement pour le % de non anglophone. La distribution après légèrement moins éloignée d’une loi normale (même si c’est très loin d’être parfait).
Ré-estimons le modèle sur la base avec nos variables transformées et accolons ces résultats à ceux obtenus sur les données brutes.
reg_log<-reg_(testscr~str+el_pct,don=dat_log,opt='col_sd',
lab=c('constante',"taux d'encadrement",
'% de non angl'))
tab<-cbind(reg_base,reg_log[,2:3])
colnames(tab)<-c('variables','base','st','log','st_')
mis_col_sd(tab)| variables | base | st | log | st_ |
|---|---|---|---|---|
| constante | 686.032 | *** | 6.585 | *** |
| ( 8.697 ) | ( 0.047 ) | |||
| taux d'encadrement | -1.101 | ** | -0.024 | ** |
| ( 0.431 ) | ( 0.015 ) | |||
| % de non angl | -0.65 | *** | -0.013 | *** |
| ( 0.031 ) | ( 0.001 ) | |||
| Adj_R2 | 0.4237 | 0.346 | ||
| F de fisher | 155.01 | *** | 111.83 | *** |
| nobs | 420 | 420 |
Observons la forme des résidus de cette régression avec un nouvel histogramme.
hist_dist_(var1 = lm(testscr~str+el_pct,data=dat_log)$residu,
df=dat_log,nom="residus")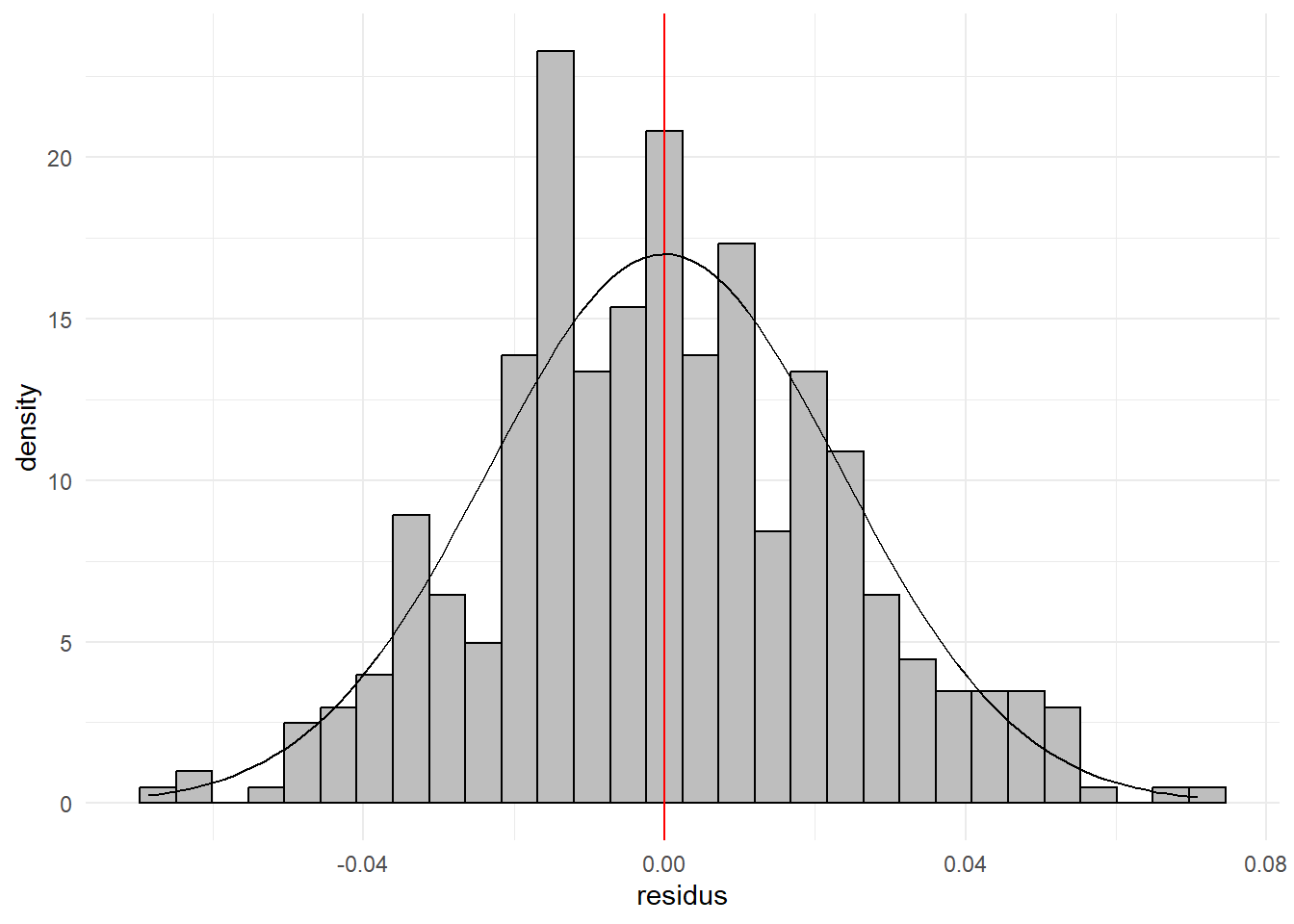
On est encore une fois (sans grande surprise) très proche d’une loi normale. On peut le voir également avec les skewness et kurtosis.
c(sk=skewness(lm(testscr~str+el_pct,data=dat_log)$residu),
kurt=kurtosis(lm(testscr~str+el_pct,data=dat_log)$residu))## sk kurt
## 0.1523924 3.0041134la winsorisation des variables
Une autre manière de traiter les difficultés associées à la forme des variables notamment la présence d’observations atypiques (extrêmes), il s’agit de la winsorisation. En l’appliquant, on remplace les valeurs les plus extrêmes (les plus grandes et les plus petites) par des moins extrêmes. En général, on remplace les données situées en dessous du cinquième percentile par ce percentile et celles situées au dessus de quatre vingt cinquième percentile par celui-ci.
Le package DescTools propose une fonction Winsorize(). Utilisons-la sur nos données.
dat_win<-dat %>% mutate(
testscr=Winsorize(testscr,probs = c(0.05, 0.95)),
str=Winsorize(str,probs = c(0.05, 0.95)),
el_pct=Winsorize(el_pct,probs = c(0.05, 0.95)))Observons une nouvelle fois les conséquences de cette transformations sur nos données à partir des histogrammes.
G1<-hist_dist_(var1 = testscr,df=dat_win,nom="score")
G2<-hist_dist_(var1 = str,df=dat_win,nom="taux d'encadrement")
G3<-hist_dist_(var1 = el_pct,df=dat_win,nom="% de non angl")
G1/(G2+G3)
L’étendu des variables a été réduite et une concentration importante apparaît aux bornes.
Ré-estimons le modèle avec les variables winsorisées.
reg_win<-reg_(testscr~str+el_pct,don=dat_win,opt='col_sd',
lab=c('constante',"taux d'encadrement",
'% de non angl'))
tab<-cbind(reg_base,reg_log[,2:3],reg_win[,2:3])
colnames(tab)<-c('variables','base','st','log','st_','win','st__')
mis_col_sd(tab)| variables | base | st | log | st_ | win | st__ |
|---|---|---|---|---|---|---|
| constante | 686.032 | *** | 6.585 | *** | 681.784 | *** |
| ( 8.697 ) | ( 0.047 ) | ( 8.512 ) | ||||
| taux d'encadrement | -1.101 | ** | -0.024 | ** | -0.896 | ** |
| ( 0.431 ) | ( 0.015 ) | ( 0.428 ) | ||||
| % de non angl | -0.65 | *** | -0.013 | *** | -0.673 | *** |
| ( 0.031 ) | ( 0.001 ) | ( 0.031 ) | ||||
| Adj_R2 | 0.4237 | 0.346 | 0.4389 | |||
| F de fisher | 155.01 | *** | 111.83 | *** | 164.87 | *** |
| nobs | 420 | 420 | 420 |
Examinons les résidus.
hist_dist_(var1 = lm(testscr~str+el_pct,data=dat_win)$residu,df=dat_win,
nom="residus")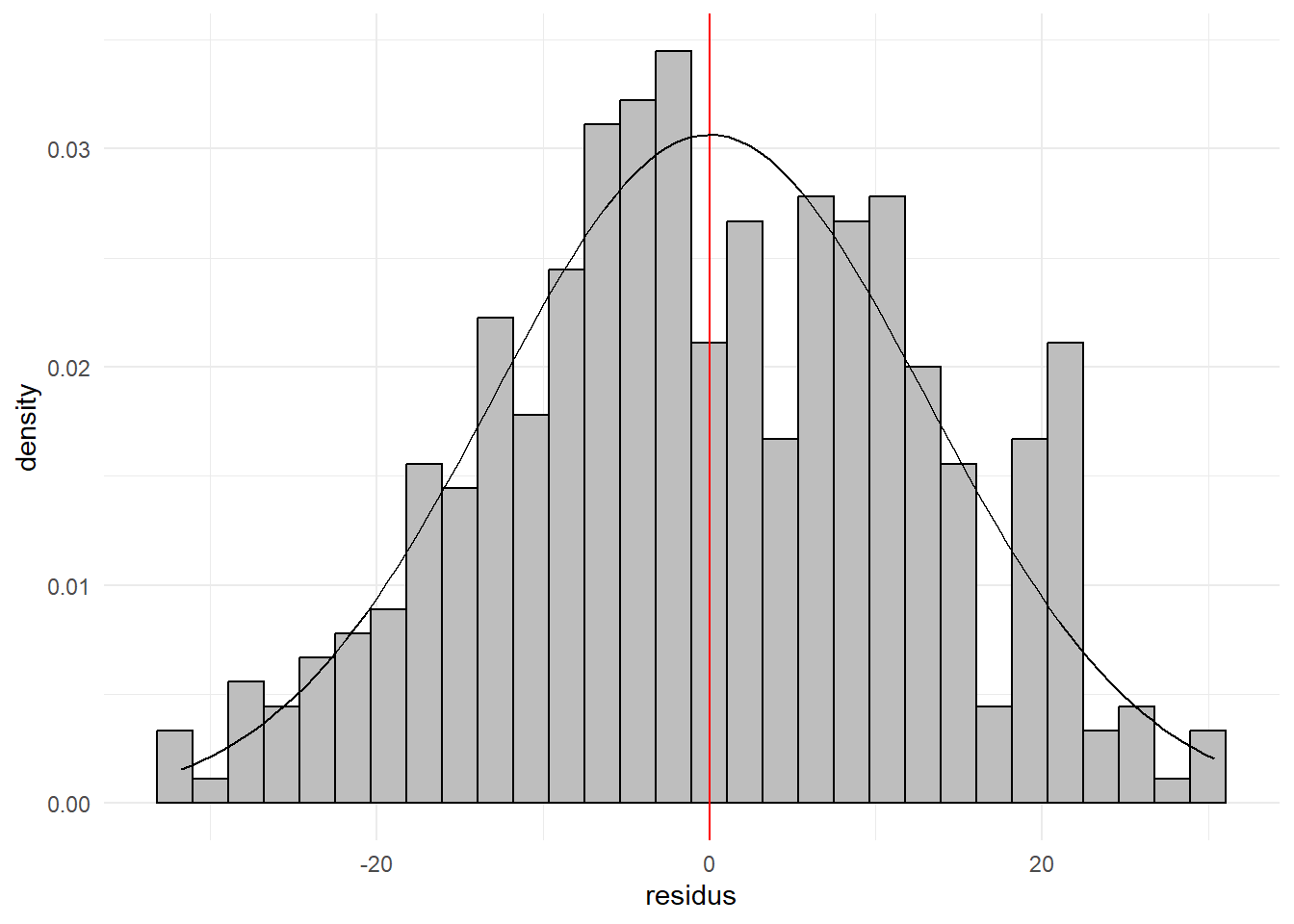
On est encore une fois (sans grande surprise) très proche d’une loi normale. On peut le voir également avec les skewness. Les choses sont moins nettes sur la kurtosis puisque l’on a renforcé les valeurs correspondant au 5ème et 95ème percentile.
c(sk=skewness(lm(testscr~str+el_pct,data=dat_win)$residu),
kurt=kurtosis(lm(testscr~str+el_pct,data=dat_win)$residu))## sk kurt
## -0.03580107 2.46159159