Dans ce dernier post de la série, nous allons aborder la question des problèmes d’hétérosdasticité qui peuvent affecter les régressions estimées via les moindres carrés ordinaires (MCO). Il s’agit des cas où le nuages de points représentant les erreurs d’estimation en fonction des valeurs de la variable explicative présente une forme d’hétérosgénéité. Cette forme indique que la variance de l’erreur en fonction de ces valeurs n’est pas homogène. Dans ce cas, les MCO ne sont plus BLUE (Best Linear Unbiased Estimator). Ils demeurent sans biais, mais l’erreur type est fausse. Cela signifie que les tests statistiques portant sur les coefficients sont moins fiables.
Commençons par charger les packages nécessaires à nos différents traitements. Notez ici la présence de deux nouveaux éléments lmtest et sandwich. Le premier comprend une série de fonctions permettant de tester différentes hypothèses associées au modèle de régression linéaire. Le second permet de traiter la matrice variance covariance de la régression pour corriger les tests portant sur les coefficients de l’hétéroscédasticité.
library(tidyverse)
library(haven)
library(lmtest)
library(sandwich)
library(gt)Chargeons les données portant sur les écoles californiennes que nous avons utilisé dans les précédents post et que vous pouvez retrouver ici.
caschool <- read_dta("caschool.dta")Procédons à la régression de testscor (le score moyen obtenu par l’école considérée au test de niveau de ses élèves) sur la variable str (le ratio nombre d’élèves par enseignant dans l’école).
reg_1<-lm(testscr~str,data=caschool)Observons les résultats au travers de la fonction summary().
summary(reg_1)##
## Call:
## lm(formula = testscr ~ str, data = caschool)
##
## Residuals:
## Min 1Q Median 3Q Max
## -47.727 -14.251 0.483 12.822 48.540
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 698.9330 9.4675 73.825 < 2e-16 ***
## str -2.2798 0.4798 -4.751 2.78e-06 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 18.58 on 418 degrees of freedom
## Multiple R-squared: 0.05124, Adjusted R-squared: 0.04897
## F-statistic: 22.58 on 1 and 418 DF, p-value: 2.783e-06Le coefficient associé à la variable explicative str apparaît négatif et statistiquement différent de zéro. Mais le test utilisé est-il assez rigoureux.
Pour le savoir, vérifions si la régression souffre d’hétéroscédasticité. Commençons par examiner le lien entre les résidus de la régression et la variable explicative au travers d’un graphe.
res_<-data.frame(str=caschool$str,resid=reg_1$residuals)
ggplot(data=res_,aes(x=str,y=resid))+
geom_point(size=0.5)+
geom_smooth(method='lm',size=0.5)+
coord_cartesian(expand=FALSE,xlim=c(13.5,26),ylim=c(-50,50))+
theme_minimal()## Warning: Using `size` aesthetic for lines was deprecated in ggplot2 3.4.0.
## ℹ Please use `linewidth` instead.## `geom_smooth()` using formula = 'y ~ x'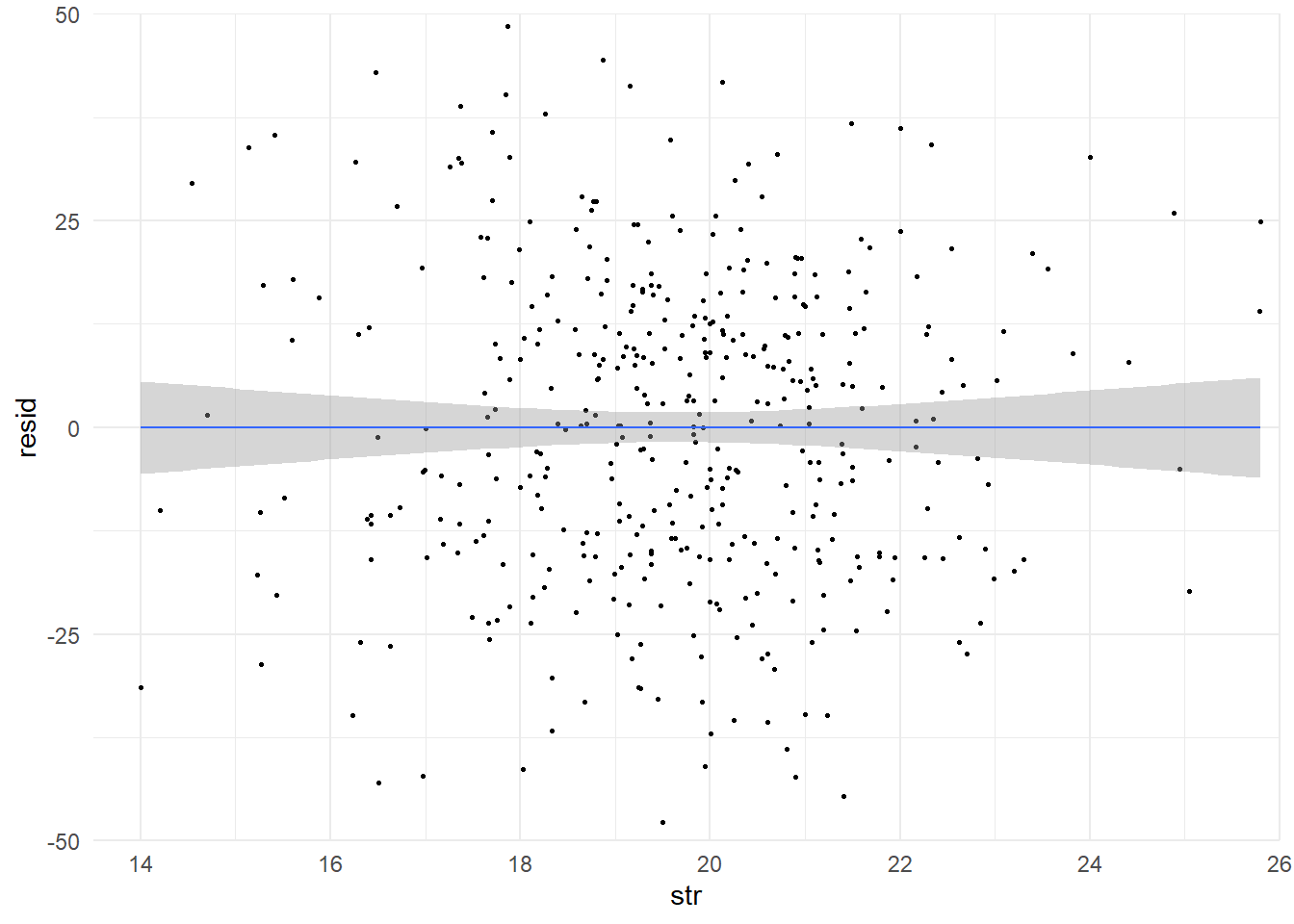
La droite passant au milieu du nuage le résume. La bande grise présente un intervalle de confiance pour chaque valeur. Son élargissement aux extrémités laisse penser à la présence d’hétéroscédasticité.
Approfondissons la question à partir de la procédure proposée par Breusch et Pagan en 1979. Commençons par régresser le carré des résidus de notre régression sur la variable explicative. Stockons le résumé de la régression dans un objet et affichons son contenu.
sum<-summary(lm(resid^2~str,data=res_))
sum##
## Call:
## lm(formula = resid^2 ~ str, data = res_)
##
## Residuals:
## Min 1Q Median 3Q Max
## -472.6 -279.4 -153.4 115.6 1965.3
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 865.47 216.82 3.992 7.75e-05 ***
## str -26.57 10.99 -2.418 0.016 *
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 425.5 on 418 degrees of freedom
## Multiple R-squared: 0.01379, Adjusted R-squared: 0.01143
## F-statistic: 5.847 on 1 and 418 DF, p-value: 0.01603Dans le cadre multivarié, si au moins une des variables est statistiquement différente de zéro. Cela signifie qu’on a des variables explicatives influences les résidus, bref que l’on est face à un problème d’hétéroscédasticité.
Pour tester cela rapidement, il suffit de reprendre le test de Fisher de la régression. Ici, si l’on fixe la limite le risque d’erreur de type 1 (rejeter H0 alors qu’elle est vraie) à 5%. Avec une p-value de 0,01603, on rejette H0 l’hypothèse selon laquelle tous les coefficients de la régression de nos résidus sont égale à 0. Au moins un des coefficient est statistiquement différent de zéro. On a bien de l’hétéroscédasticité.
La version le plus courante de ce test, le test de Breusch-Pagna, utilise procédure très légèrement différente. A la place de la statitistique de fisher, elle utilise BP qui correspond à la multiplication du \(R^2\) de la régression par le nombre d’observations. Celle-ci suit une loi du khi2 dont le nombre de degrés de liberté correspond au nombre de coefficients (constante inclus) moins 1.
420*sum$r.squared## [1] 5.7935971-pchisq(420*sum$r.squared,df=2-1)## [1] 0.01608464On aboutie sous surprise au même résultat. L’hypothèse d’homoscédasticité est rejété.
La fonction bptest() du package lmtest permet de réaliser le test plus rapidement.
bptest(reg_1)##
## studentized Breusch-Pagan test
##
## data: reg_1
## BP = 5.7936, df = 1, p-value = 0.01608Il existe d’autres test d’hétéroscédasticité comme le test de White. Mais ce n’est pas l’objet principal de ce post.
Maintenant que nous avons confirmation du problème que faire?
Utilisons un correctif pour nos erreurs types de manière à ajuster les test sur les coefficients. Encore une fois, il en existe plusieurs nous contenterons ici de celui mobilisé par défaut dans Stata.
Pour cela, nous utiliserons la fonction coeftest() du package lmtest qui permet de faire les tests de Student sur les coefficients et qui propose avec l’option vcov d’utiliser une matrice variance-covariance modifiée.
Utilisons-la simplement sur notre régression sans rien spécifier.
coeftest(reg_1)##
## t test of coefficients:
##
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 698.93295 9.46749 73.8245 < 2.2e-16 ***
## str -2.27981 0.47983 -4.7513 2.783e-06 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1On retrouve les mêmes résultats que dans la sortie issue de la fonction summary(). L’erreur type est obtenu sur la base de la matrice variance covariance suivante:
sum$cov.unscaled## (Intercept) str
## (Intercept) 0.25961704 -0.013097277
## str -0.01309728 0.000666853L’erreur type des coefficients est obtenu à partir de la formule suivante:
\[\sqrt{(M_{cov.res}.X^{T}.(s^2.I_n).X .M_{cov.res}).I_p}\]
Celle-ci peut paraître impressionnante. Mais elle se calcule assez facilement avec R. On retrouve de chaque côté la matrice variance-covariance des erreurs qui prend en sandwich une expression où l’on trouve la transposée de la matrice des variables du modèle, un matrice avec pour diagonal la variance des résidus du modèle et la matrice des variables du modèle. I représente la matrice identité si elle est indicée n sa taille correspond à celle de l’échantillon et si elle est indicée p aux nombre de paramètre du modèle. Appliquons-la.
s2 <- summary(reg_1)$sigma^2
X <- model.matrix(reg_1)
vce <- sum$cov.unscaled %*% (t(X) %*% (s2*diag(420)) %*% X) %*%
sum$cov.unscaled
sqrt(diag(vce))## (Intercept) str
## 9.4674914 0.4798256On retrouve bien les erreurs types du modèle. Le test de Breusch-Pagan indique que nous avons de l’hétéroscédasticité et donc qu’elle doivent être ajustées.
Pour cela, nous travaillerons avec le centre de l’expression (le milieu du sandwich, la garniture). Nous remplacerons \(s^2\) par une expression adaptée. Encore une fois, ici , plusieurs solutions sont possibles. Néanmoins, nous n’en illustrerons qu’une. Celle retenu par défaut dans Stata lorsque l’on indique robust (ou simplement r) dans les options de regress (aprés la virgule).
Ce correctif est nommé HC1 (Heteroscedasticity Consistent 1). Il consiste à remplacer la variance des erreurs par :
\[HC1=\frac{n}{n-p}res^2\]
Le carré des résidus ajusté par le ratio du nombre d’observation sur le nombre de degrés de liberté (nombre d’observation moins le nombre de paramètres). Appliquons le correctif à notre calcul étendu.
hc1 <- ((420)/(420-2))*reg_1$residuals^2
X <- model.matrix(reg_1)
vce <- sum$cov.unscaled %*% (t(X) %*% (hc1*diag(420)) %*% X) %*%
sum$cov.unscaled
sqrt(diag(vce))## (Intercept) str
## 10.3643599 0.5194892Le même résultat peut être obtenu plus rapidement en utilisant la fonction vcovHC() du package sandwich.
sqrt(diag(vcovHC(reg_1, "HC1")))## (Intercept) str
## 10.3643599 0.5194892Les tests sur les coefficients réalisés sur la base de cet ajustement peut être obtenu avec coeftest() en incluant dans l’option vcov la matrice variance-covariance modifiée issue de vcovHC().
coeftest(reg_1,vcov=vcovHC(reg_1, "HC1"))##
## t test of coefficients:
##
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 698.93295 10.36436 67.4362 < 2.2e-16 ***
## str -2.27981 0.51949 -4.3886 1.447e-05 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1Vous noterez ici que l’on aboutit à la même conclusion que si l’on ne fait pas à l’ajustement ce n’est pas toujours le cas. Quoiqu’il en soit le nouveau test est plus rigoureux dans la mesure où il teint compte du l’absence d’homogénéité de la variance pour mettre en oeuvre les tests de Student.