Pour cette seconde note “rapide” sur la méthode Difference-in-Difference, nous allons considérer un exemple tiré du chapitre 18 du livre The Effect de Nick Huntinghton-Klein, que vous trouverez ici (mais qui est également disponible en version papier dans toutes les bonnes librairies). Il s’agit d’une réplication d’une étude réalisée par Kessler and Roth (2014) plus spécifiquement d’une partie du tableau 2 que l’on peut trouver à la page 9.
Dans les papiers, les auteurs s’intéressent à la proportion d’individus acceptant d’être donneur d’organes aux USA. Les Etats-Unis sont un Etat fédéral. Il en résulte que les législations peuvent varier d’un Etat à l’autre. Dans la plus part d’entre eux, les individus sont supposés ne pas être donneur (c’est le choix par défaut). Néanmoins, lorsqu’ils réalisent les formalités pour obtenir leur permis de conduire, on leur donne la possibilité d’opter pour faire partir du programme de donneurs d’organes. S’ils cochent la casse, en cas de décès, leurs organes pourront être prélevés afin de sauver des vies. Le taux de donneurs aux Etat-Unis est plus faible que celui constaté dans d’autres pays notamment ceux où le choix de ne pas être donneur doit être exprimé plutôt que l’inverse. Les auteurs s’interrogent alors sur l’effet de la formulation de l’option sur le choix d’être donateur potentiel ou non.
En Juillet 2011, la Californie décide de changer la formulation de l’option proposée pour que l’on ne soit plus sur un non par défaut simple. L’ancienne formulation proposée de cocher soit une casse d’acceptation de la participation au programme soit une pour faire un don pécuniaire. La nouvelle ajoute une casse à cocher pour indiquer que l’on ne souhaite pas être donneur (voir figure 1 p.7 du papier). Ici, le choix de ne pas être donneur peut ainsi s’exprimer de manière active.
On a ici un cadre d’expérience permettant d’identifier (ou de chercher à identifier) l’effet du changement de formulation via une approche Difference-in-Difference avec pour traité la Californie et comme groupe de contrôle les Etats qui n’ont pas changé de formulation (ici 26 Etats).
Chargeons les packages et les données
Avant d’aller plus loin, chargeons les différents packages que nous allons mobiliser.
library(tidyverse)
library(scales)
library(zoo)
library(fixest)
library(lmtest)
library(sandwich)Les données sont disponibles dans la package causaldata. La base associée s’appelle organe_donations.
od <- causaldata::organ_donations
head(od)## # A tibble: 6 × 4
## State Quarter Rate Quarter_Num
## <chr> <chr> <dbl> <int>
## 1 Alaska Q42010 0.75 1
## 2 Alaska Q12011 0.77 2
## 3 Alaska Q22011 0.77 3
## 4 Alaska Q32011 0.78 4
## 5 Alaska Q42011 0.78 5
## 6 Alaska Q12012 0.79 6Pratiquons quelques transformations et mises en forme pour nous faciliter la tache par la suite. Marquons la Californie dans une variable binaire et passons les Quarter en format temps.
od<-od %>%
mutate(californie=State=="California",
Annee=substring(Quarter,first=3),
trim=substring(Quarter,first=2,last=2),
An_trim=paste0(Annee,".",trim),
Trimestre=yq(An_trim)) %>%
select(-Annee,-trim,-An_trim)Analyses préliminaires
Avant d’aller plus loin, voyons un peu ce que donne notre variable expliquée sur l’ensemble de la période d’étude pour chaque Etat. Pour ce faire, réalisons un strip chart en s’assurant de marquer spécifiquement les observations pour la Californie et la date du changement dans la formulation de la question.
G1<-ggplot(data=od,aes(x=Trimestre+30,y=Rate,
colour=californie,
shape=californie,
alpha=californie))+
geom_jitter(width = 30)+
geom_vline(xintercept = as.Date("2011-07-01"),
linewidth=0.1,linetype="dashed")+
geom_text(aes(label="Californie",
x=as.Date("2012-02-01"),
y=0.2))+
labs(title = "Taux de dons d'organes
en Californie et dans les autres Etats",
x="Trimestre")+
scale_x_date(labels=label_date(format = "%b %Y"))+
scale_y_continuous(labels = label_percent())+
scale_shape_manual(values=c(1, 16))+
scale_colour_manual(values=c("Black","Black"))+
scale_alpha_manual(values=c(0.5,1))+
theme_minimal()+
theme(
plot.title = element_text(hjust=0.5,face="bold"),
axis.title.y = element_blank(),
axis.line = element_line(color="black",
linewidth=0.1),
axis.ticks = element_line(color="black",
linewidth=0.1),
panel.grid = element_blank(),
legend.position="none"
)
G1
On note d’une part que quelle que soit la date considérée la Californie fait partie des Etats pour lesquels le taux de donneurs est le plus bas, et d’autre part que ce taux ne varie pas beaucoup sur l’ensemble de la période d’étude.
Voyons cela de manière plus précise au travers du tableau des moyennes (Control/Traité/Avant/Après).
moy_av_c<-mean(filter(od,
State!="California"&
Trimestre<as.Date("2011-07-01"))$Rate)
moy_ap_c<-mean(filter(od,
State!="California"&
Trimestre>=as.Date("2011-07-01"))$Rate)
moy_av_t<-mean(filter(od,
State=="California"&
Trimestre<as.Date("2011-07-01"))$Rate)
moy_ap_t<-mean(filter(od,
State=="California"&
Trimestre>=as.Date("2011-07-01"))$Rate)
table_moy<-data.frame(Avant=c(moy_av_c,moy_av_t),
Apres=c(moy_ap_c,moy_ap_t))
row.names(table_moy)<-c("Control","Traité (Californie)")
table_moy## Avant Apres
## Control 0.4449308 0.4588564
## Traité (Californie) 0.2713333 0.2628000La tableau confirme que la moyenne du taux de donneur en Californie est plus faible que celle du groupe de contrôle. Cette moyenne augmente très légèrement après le juillet 2011 pour le groupe de contrôle mais diminue légèrement pour la Californie. Visualisons les choses sur notre strip chart.
G1+
geom_segment(aes(x=as.Date("2010-10-01"),
xend=as.Date("2011-07-01"),
y= moy_av_c,
yend=moy_av_c),linewidth=0.7,
linetype="dashed",color="#817D7C")+
geom_segment(aes(x=as.Date("2011-07-01"),
xend=as.Date("2012-01-01")+60,
y= moy_ap_c,
yend=moy_ap_c),linewidth=0.7,
linetype="dashed",color="#817D7C")+
geom_segment(aes(x=as.Date("2010-10-01"),
xend=as.Date("2011-07-01"),
y= moy_av_t,
yend=moy_av_t),linewidth=0.7,
color="black")+
geom_segment(aes(x=as.Date("2011-07-01"),
xend=as.Date("2012-01-01")+60,
y= moy_ap_t,
yend=moy_ap_t),linewidth=0.7,
color="black")
Établissons les différences avant et après juillet 2011 pour les deux groupes.
table_d<-table_moy %>%
mutate(dif_av_a_p=Apres-Avant)
table_d %>% round(digits=3)## Avant Apres dif_av_a_p
## Control 0.445 0.459 0.014
## Traité (Californie) 0.271 0.263 -0.009Elles confirment la faible évolution positive du groupe de contrôle et la faible évolution négative pour la Californie. A partir de là, il est facile d’établir l’effet du traitement au travers la double différence (la difference-in-difference).
table_d$dif_av_a_p[2]-table_d$dif_av_a_p[1]## [1] -0.02245897La modification opérée en Californie à conduit à réduire le taux de donneurs de prés de 2,246%.
Analyse de régression
La table des moyennes nous permet d’avoir une valeur pour l’effet du traitement mais elle ne fournit par de tests statistiques sur cette valeur. Pour y remédier, estimons l’effet du traitement via une régression.
Pour cela, nous pouvons utiliser la spécification classique.
\[ outcome_{i,t}=\alpha+\beta_1.traite_i+\beta_2.post_t+\beta_3.traite_i\times{post_t}+\epsilon \]
Le modèle est estimé par les moindres carrés ordinaires. La variable traite correspond ici à notre variable Californie. Il nous faut coder la variable post. Appelons la ap (pour après).
od<-od %>%
mutate(ap=Trimestre>=as.Date("2011-07-01"))Maintenant que nous avons nos deux variables explicatives, nous pouvons les utiliser dans la régression avec leur interaction.
reg_1<-lm(Rate ~ californie+ap+californie*ap,
data=od)
summary(reg_1)##
## Call:
## lm(formula = Rate ~ californie + ap + californie * ap, data = od)
##
## Residuals:
## Min 1Q Median 3Q Max
## -0.33596 -0.09975 -0.00291 0.11394 0.33114
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 0.44493 0.01705 26.101 <2e-16 ***
## californieTRUE -0.17360 0.08858 -1.960 0.0518 .
## apTRUE 0.01393 0.02411 0.578 0.5643
## californieTRUE:apTRUE -0.02246 0.12527 -0.179 0.8579
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 0.1506 on 158 degrees of freedom
## Multiple R-squared: 0.05416, Adjusted R-squared: 0.0362
## F-statistic: 3.015 on 3 and 158 DF, p-value: 0.03172La valeur du coefficient associé au terme d’interaction correspond à l’arrondi prés à la difference-in-difference. Néanmoins, il n’apparaît pas statistiquement différent de zéro dans cette configuration du test. Isolons ce résultat en utilisant la fonction coeftest() du package lmtest.
coeftest(reg_1)[4,]## Estimate Std. Error t value Pr(>|t|)
## -0.02245897 0.12526689 -0.17928898 0.85794051On retrouve bien notre estimation primaire. Le test pratiqué a le défaut de ne pas prendre en compte la structure de la variabilité des valeurs. Celle-ci est plus importante dans sa dimension individuelle (Etat) que dans sa dimension temporelle. Aussi, un test considérant un clustering de la variable State apparaît plus approprié. Générons-le en spécifiant la matrice variance-covariance correspondant. Celle-ci est établie à partir de la fonction vcovCL() du package sandwich.
coeftest(reg_1,
vcov. = vcovCL(reg_1,
cluster= ~State))[4,]## Estimate Std. Error t value Pr(>|t|)
## -0.0224589744 0.0060727451 -3.6983232144 0.0002990217Le test cette fois permet largement de rejeter l’hypothèse d’absence d’effet du traitement (avec une p-value de moins de 0,03%).
On peut de manière équivalente estimer la difference-in-difference en utilisant une spécification alternative basé sur les two-way-fixed-effect.
\[ outcome_{i,t}=\alpha_i+\alpha_t+\beta.traited+\epsilon \]
On a ainsi un premier effet fixe individuel (contrôlant ici pour l’Etat) et un second effet fixe cette fois temporelle (contrôlant ici pour le trimestre). La variable traited est ici une variable binaire prenant la valeur 1 pour le groupe des traités une fois qu’ils ont reçu le traitement (la Californie à partir de juillet 2011). Codons cette variable.
od <- od %>%
mutate(Treated = State == 'California' &
Trimestre>=as.Date("2011-07-01"))Reste alors à estimer la régression. Pour cela, le plus simple est d’utiliser la fonction feols() (fixed effects OLS) du package fixest. Indiquons pour le tableau de régression que l’on considère un clustering individuel pour la calcul de l’erreur standard. Faisons-le en indiquant dans l’option vcov “cluster” (il prend la premier effet fixe comme référence).
clfe <- feols(Rate ~ Treated | State + Quarter,
data = od)
summary(clfe,vcov = "cluster")## OLS estimation, Dep. Var.: Rate
## Observations: 162
## Fixed-effects: State: 27, Quarter: 6
## Standard-errors: Clustered (State)
## Estimate Std. Error t value Pr(>|t|)
## TreatedTRUE -0.022459 0.006131 -3.66304 0.0011185 **
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## RMSE: 0.021982 Adj. R2: 0.974196
## Within R2: 0.009221On retrouve la même estimation de l’effet qui est statistiquement significatif. Cette estimation peut également être obtenue à partir de la fonction lm() de R base en portant State et Quarter comme variable effet fixe (série de dummies). N’affichons que la ligne qui nous intéresse dans le rendu de la régression, la dernière du tableau des coefficients.
reg_2<-lm(Rate~State+Quarter+Treated, data=od)
summary(reg_2)$coefficient[nrow(summary(reg_2)$coefficient),]## Estimate Std. Error t value Pr(>|t|)
## -0.02245897 0.02049686 -1.09572767 0.27523942On retrouve le coefficient correspondant à l’effet du traitement mais il apparaît non significatif à partir du test sans cluster. Réalisons le test sur le coefficient avec cluster sur State.
coeftest(reg_2,vcov. = vcovCL(reg_2,
cluster= ~State))[33,]## Estimate Std. Error t value Pr(>|t|)
## -0.022458974 0.006720766 -3.341728598 0.001089546Avec le clustering, on constate que le coefficient est bien statistiquement différent de 0.
Le traitement apparaît bien avoir un effet même si celui-ci est faible (une réduction de 2,24 points de pourcentage du taux de donneurs).
Examinons la parallel trend hypothesis
L’effet du traitement est identifié à la seule condition que l’hypothèse de tendance parallèle d’évolution de l’outcome entre le groupe traité et le groupe de contrôle en l’absence de traitement soit tenue. Par définition, celle-ci n’est pas testable dans la mesure où l’on ne peut pas observer l’évolution des traités s’ils n’avaient pas été traités. Néanmoins, cela ne signifie pas que l’on ne peut rien faire pour convaincre qu’elle est plausible. En l’absence de parallel trend, on ne peut être sûr que le changement constaté sur le groupe des traités est dû au traitement. Mais, même s’il n’y a pas de test définitif, on peut essayer de convaincre de la plausibilité du parallel trend au travers notamment de tests sur la tendance pré-traitement ou de tests placebo.
Commençons par la tendance pré-traitement. Il y a basiquement deux manières de procéder. La première est simplement d’observer l’évolution des moyennes de l’outcome pour les traités et non traités au travers d’un graphe. Pour le réaliser, calculons les moyennes trimestrielles sur le groupe de contrôle et la Californie.
par_1<-od %>%
group_by(californie,Trimestre) %>%
summarise(moy_=mean(Rate))
par_1## # A tibble: 12 × 3
## # Groups: californie [2]
## californie Trimestre moy_
## <lgl> <date> <dbl>
## 1 FALSE 2010-10-01 0.444
## 2 FALSE 2011-01-01 0.442
## 3 FALSE 2011-04-01 0.449
## 4 FALSE 2011-07-01 0.460
## 5 FALSE 2011-10-01 0.456
## 6 FALSE 2012-01-01 0.461
## 7 TRUE 2010-10-01 0.267
## 8 TRUE 2011-01-01 0.273
## 9 TRUE 2011-04-01 0.274
## 10 TRUE 2011-07-01 0.264
## 11 TRUE 2011-10-01 0.261
## 12 TRUE 2012-01-01 0.264
Créons le graphe.
ggplot(data=par_1,aes(x=Trimestre,y=moy_,
colour=californie,
shape=californie,
alpha=californie))+
geom_point()+
geom_line()+
geom_vline(xintercept = as.Date("2011-07-01"),
linewidth=0.1,linetype="dashed")+
geom_text(aes(label="Californie",
x=as.Date("2012-02-01"),
y=0.25))+
labs(title = "Taux de dons d'organes
en Californie et dans les autres Etats",
x="Trimestre")+
scale_x_date(labels=label_date(format = "%b %Y"))+
scale_y_continuous(labels = label_percent())+
scale_shape_manual(values=c(1, 16))+
scale_colour_manual(values=c("Black","Black"))+
scale_alpha_manual(values=c(0.5,1))+
theme_minimal()+
theme(
plot.title = element_text(hjust=0.5,face="bold"),
axis.title.y = element_blank(),
axis.line = element_line(color="black",
linewidth=0.1),
axis.ticks = element_line(color="black",
linewidth=0.1),
panel.grid = element_blank(),
legend.position="none"
)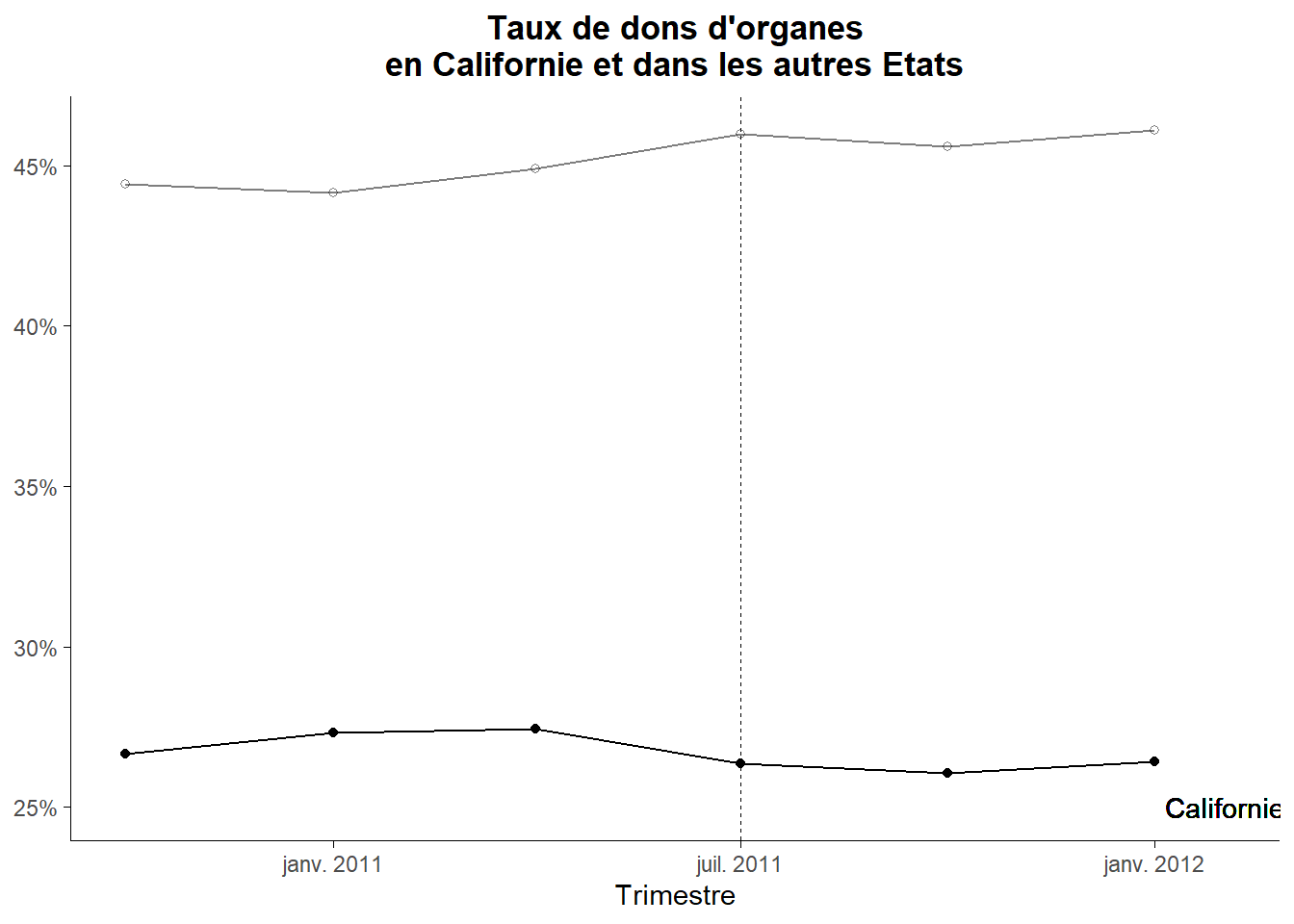
L’ensemble semble assez parallèle sur la période pré-traitement. Néanmoins, nous aimerions avoir un test statistique. Le plus simple consiste à estimer sur le période pré-traitement le modèle suivant:
\[ outcome_{i,t}=\alpha+\beta_1.periode+\beta_2.periode\times{Traite}+\epsilon \]
Où periode est l’indexation temporaire des observations sur la période et Traite l’affectation au groupe des traités (ici californie). Si \(\beta_2\) est statistiquement significatif, on peut questionner la parallel trend pré-traitement. La pente de la droite outcome/periode est différente entre les traités et les non traités.
reg_p1<-lm(Rate~Quarter_Num+Quarter_Num*californie,
data=filter(od,Trimestre<as.Date("2011-07-01")))
coeftest(reg_p1)[3,]## Estimate Std. Error t value Pr(>|t|)
## -0.1765397 0.2446478 -0.7216077 0.4727212Ici, il semble que la parallel trend pre-traitement tienne. La spécification retenu dans le test que nous venons de pratiquer est la plus simple possible. On peut envisager des formes plus complexes en ajoutant des termes polynomiaux ou d’autres éléments associés à une non linéarité de la tendance (qui peut être parallèle en étant non-linéaire).
Si on trouve qu’il y a une tendance différente (pré-traitement), on cherchera en quoi elle est différente. Est-ce qu’elle est juste légèrement différente mais que cette différence est statistiquement significative du fait de la taille de l’échantillon? Est ce que les tendances divergent à cause de brèves sous périodes il y a quelques années? Il faut comprendre d’où vient le décalage.
Lorsque le test de pré-tendance échoue, certains chercheurs cherchent à sauver leur travail en contrôlant pour la tendance en incluant une variable temps à la place des effets fixes temps dans régression. Cependant, cela n’est pas sans poser problème. Ce contrôle peut masquer une partir de l’effet du traitement tout particulièrement lorsque les effets sont de plus en plus fort ou de plus en plus faible à mesure que le temps passe (Wolfers (2006)). Il y a aussi des manières de contrôler uniquement pour les tendances pré-traitement qui consistent à réaliser une sorte d’étude d’évènements pour les groupes des traités et des non traités, mais cela peut rendre les choses encore pires (Roth (2018)).
Considérons maintenant les tests placebos. Ceux-ci peuvent se résumer en quatre étapes. Tout d’abord, on isole les observations pré-traitement. Puis, on choisi une période traitement fictive. On estime alors une difference-in-difference à partir de ces éléments fictifs. Si on trouve un effet du traitement fictif à une date où il ne devrait pas en avoir, c’est qu’il y a quelque chose qui cloche avec votre méthode de recherche (peut être une violation du parallel trend…).
Voyons cela sur nos données. Retenons deux tests placebos: le premier consistant à affecter le traitement au premier trimestre 2011 et le second consistant à l’affecter au second trimestre 2011. Commençons par limiter la base à la période pré-traitement. Puis, créons nos deux variables de traitements fictifs.
od_lim<-od %>%
filter(Trimestre<as.Date("2011-07-01")) %>%
mutate(trait_plac_1=californie==TRUE&
Quarter %in% c('Q12011','Q22011'),
trait_plac_2=californie==TRUE&
Quarter=='Q22011')Estimons les modèles Diff-in-Diff associés aux traitements placebos.
clfe1 <- feols(Rate ~ trait_plac_1 | State + Quarter,
data = od_lim)
clfe2 <- feols(Rate ~ trait_plac_2 | State + Quarter,
data = od_lim)
rbind(summary(clfe1,vcov = "cluster")$coeftable,
summary(clfe2,vcov = "cluster")$coeftable) %>%
round(digits=4)## Estimate Std. Error t value Pr(>|t|)
## trait_plac_1TRUE 0.0061 0.0051 1.1970 0.2421
## trait_plac_2TRUE -0.0017 0.0028 -0.5996 0.5540On constate que dans les deux cas les tests pour les placebos ne sont pas statistiquement significatifs ce qui est rassurant vis-à-vis du parallel trend (pre-traitement).
Une autre méthode placebo consiste, si on a plusieurs groupes de contrôle, à tous les utiliser, en excluant le groupe des traités et d’assigner de manière fictive le traitement à un des groupes de contrôle. Il s’agira alors d’estimer la Diff-in-Diff cette nouvelle base. Cette méthode est moins commune dans la mesure où elle ne traite pas du parallel trend directement. Mais c’est un test commun lorsque l’on utilise un groupe de contrôle synthétisé (Synthetic control).
Mesurer l’évolution de l’effet du traitement dans le temps
Dans l’analyse pratiquée jusqu’ici, l’effet du traitement se limite à une comparaison entre deux périodes: avant et après le traitement. Néanmoins, l’estimation en two-way-fixed-effect permet de considérer autant de périodes de temps qu’on le souhaite. Cela peut nous permettre de mettre au jour des détails utiles. Lorsque l’on est intéressé par un traitement donné, il se peut que celui-ci devienne plus ou moins efficace avec le temps ou même mette du temps avant de produire un effet. Il peut être utile dans ces cas de modifier la Diff-in-Diff pour autoriser l’effet du traitement à être différent à chaque période. Cette approche est qualifiée de dynamic treatment effects.
Une manière de pratiquer est de générer une variable temps centrée sur le traitement. Il s’agit simplement de prendre la variable temps et de lui enlever la période du traitement.
Faisons-le sur notre base où les périodes sont indexées dans Quarter_Num et la période de traitement est le quatrième trimestre. Calculons les différences et passons le résultat au format facteur puis établissons la référence sur la période juste avant le traitement (-1) : la période 3. La période -1 est la plus fréquemment utilisée comme référence dans ce type d’analyse.
od<-od %>%
mutate(dym=Quarter_Num-4,
dym_f=relevel(factor(dym),ref=3))Il s’agit alors d’estimer le modèle two-way-fixed-effect en considérant une série d’interaction entre la variable traited et les valeurs du facteur que l’on vient d’établir.
\[ outcome_{i,t}=\alpha_i+\alpha_t+\beta_1.T_{-3}.traited+\beta_2.T_{-2}.traited+\beta_3.T_0.traited+\beta_4.T_1.traited+\beta_5.T_2.traited+...+\epsilon \]
\(T_{-1}\) est ignoré pour éviter la colinéarité parfaite.
Utilisons feols() pour réaliser estimation et regardons le résultat pour les coefficients des variables d’interaction.
clfe_d_ <- feols(Rate ~ dym_f*californie |
State + Quarter_Num, data = od)## The variables 'dym_f-3', 'dym_f-2', 'dym_f0', 'dym_f1', 'dym_f2' and 'californieTRUE' have been removed because of collinearity (see $collin.var).summary(clfe_d_,vcov = "cluster")$coeftable %>%
round(digits = 4)## Estimate Std. Error t value Pr(>|t|)
## dym_f-3:californieTRUE -0.0029 0.0051 -0.5787 0.5678
## dym_f-2:californieTRUE 0.0063 0.0023 2.7788 0.0100
## dym_f0:californieTRUE -0.0216 0.0050 -4.2842 0.0002
## dym_f1:californieTRUE -0.0203 0.0045 -4.5363 0.0001
## dym_f2:californieTRUE -0.0222 0.0100 -2.2136 0.0358
## attr(,"type")
## [1] "Clustered (State)"On peut se passer de l’étape de calcule de la variable période centrée en utilisant la fonction i() qui permet d’établir des interactions en indiquant comme référence 3.
clfe_d <- feols(Rate ~ i(Quarter_Num, californie, ref = 3) |
State + Quarter_Num, data = od)
summary(clfe_d,vcov = "cluster")$coeftable %>%
round(digits = 4)## Estimate Std. Error t value Pr(>|t|)
## Quarter_Num::1:californie -0.0029 0.0051 -0.5787 0.5678
## Quarter_Num::2:californie 0.0063 0.0023 2.7788 0.0100
## Quarter_Num::4:californie -0.0216 0.0050 -4.2842 0.0002
## Quarter_Num::5:californie -0.0203 0.0045 -4.5363 0.0001
## Quarter_Num::6:californie -0.0222 0.0100 -2.2136 0.0358
## attr(,"type")
## [1] "Clustered (State)"Les coefficients s’interprétent en référence à la période juste avant le traitement (ici période -1). Pour faciliter l’interprétation, on recourt souvent à une représentation graphique basée sur les intervalles de confiance. Celle-ci s’obtient rapidement à partir de la commande coefplot().
coefplot(clfe_d)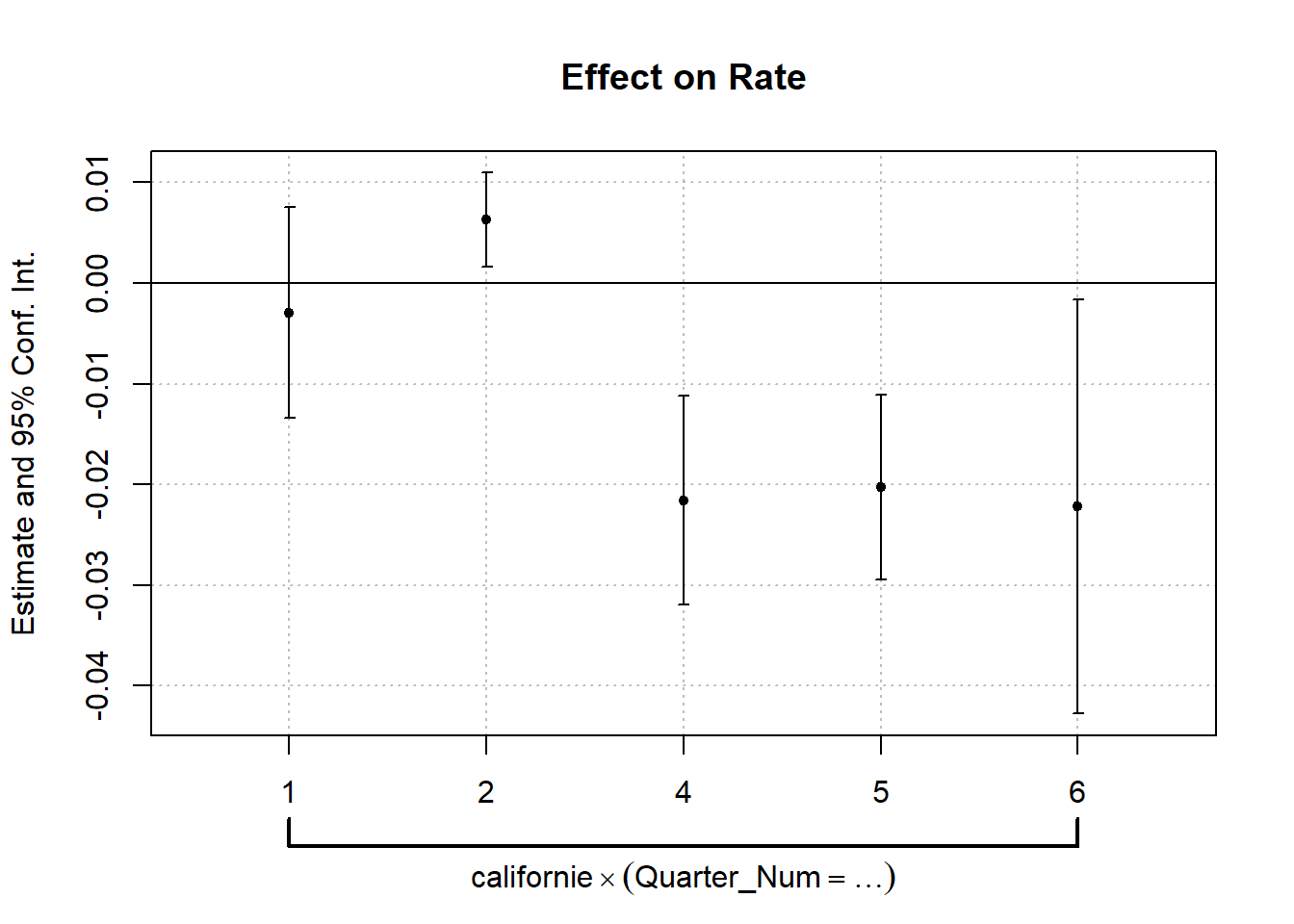
La référence est marquée par la ligne horizontale indiquant la valeur 0. Les intervalles ne croissant pas cette ligne correspondent au cas ou la valeur de l’outcome est statistiquement différent de la valeur de référence (au seuil de 95%). On voit clairement que c’est le cas de toute les observations post traitement (même si l’effet est moins net pour la troisième période après traitement). Ces observations post traitement sont les seules qui nous disent quelque chose sur celui-ci. Néanmoins, les observations prétraitement ne sont pas inutiles. Elles ne renseignent sur la parallel trend prétraitement. Idéalement elles ne seront pas statistiquement différentes de la référence (ou à défaut peu éloignées).
Le graphe produit par coefplot() n’est pas de type ggplot() ce que le rend moins flexible du point de vue de la forme. A la place, on peut utiliser ggcoef() du package ggally de manière à adapter le graphe.
GGally::ggcoef(clfe_d,
errorbar_height = 0.05,
vline_linetype = "dashed",
vline_color = "black",
vline_size = 0.2)+
annotate(geom="point",x=0,y=2.5)+
labs(title="Effet dynamique du traitement",
subtitle = "intervalle de confiance à 95%",
x="Estimation DiD ",
y="Trimestre")+
scale_y_discrete(labels=unique(od$Quarter))+
coord_flip()+
theme_minimal()+
theme(
plot.title = element_text(hjust = 0.5,face="bold"),
plot.subtitle = element_text(hjust = 0.5,face="italic"),
axis.line = element_line(color="black",
linewidth=0.15),
axis.ticks = element_line(color="black",
linewidth=0.1),
panel.grid = element_blank()
)## Registered S3 method overwritten by 'GGally':
## method from
## +.gg ggplot2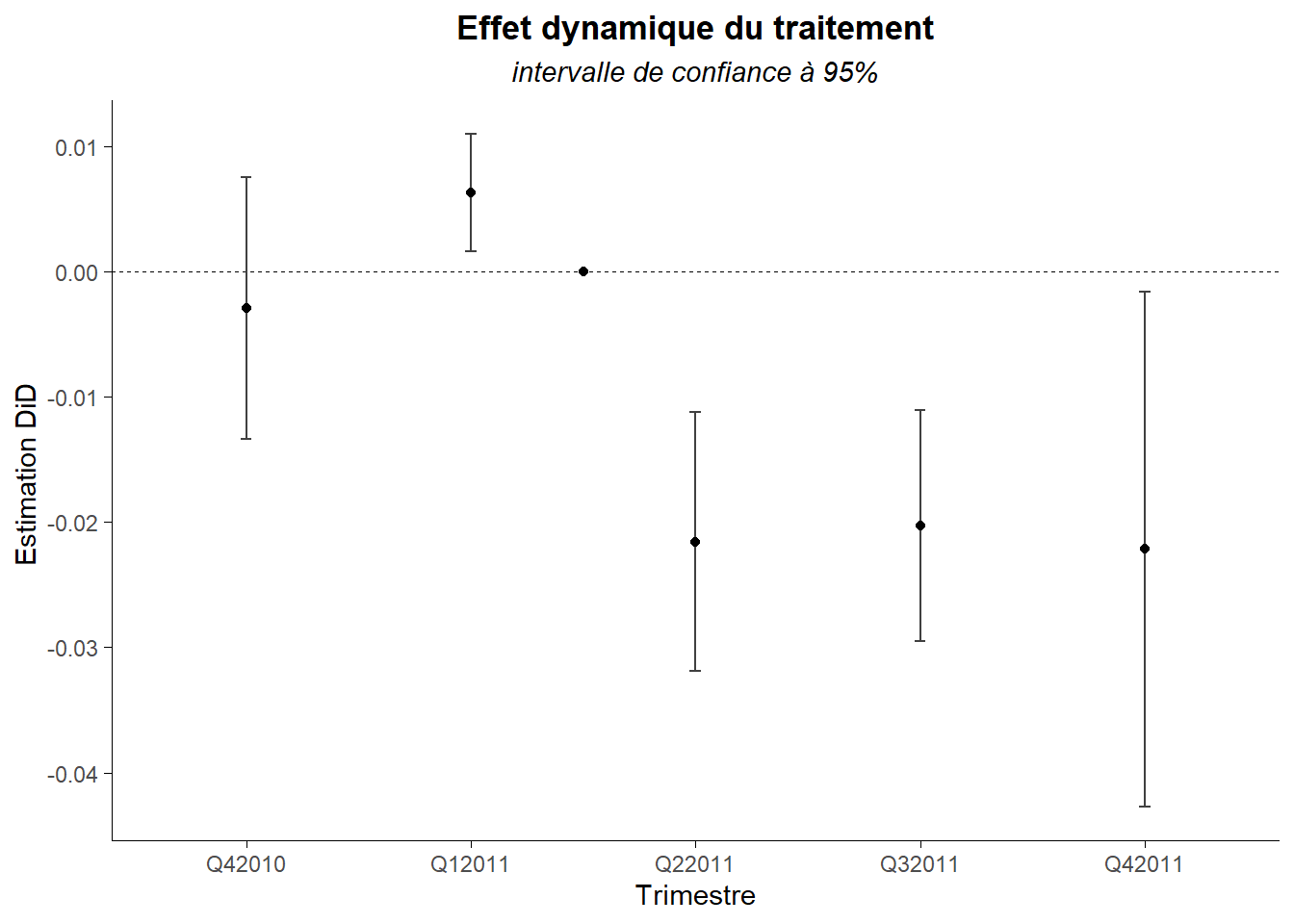
L’intervalle de confiance ici est construit sur une base de 95% (alpha de 5%). C’est la valeur par défaut. Cela peut-être simplement modifié au travers l’option conf.level. Voyons ce que cela donne avec 99% (alpha 1%).
GGally::ggcoef(clfe_d,
conf.level = 0.99,
errorbar_height = 0.05,
vline_linetype = "dashed",
vline_color = "black",
vline_size = 0.2)+
annotate(geom="point",x=0,y=2.5)+
labs(title="Effet dynamique du traitement",
subtitle = "intervalle de confiance à 99%",
x="Estimation DiD ",
y="Trimestre")+
scale_y_discrete(labels=unique(od$Quarter))+
coord_flip()+
theme_minimal()+
theme(
plot.title = element_text(hjust = 0.5,face="bold"),
plot.subtitle = element_text(hjust = 0.5,face="italic"),
axis.line = element_line(color="black",
linewidth=0.15),
axis.ticks= element_line(color="black",
linewidth=0.1),
panel.grid = element_blank()
)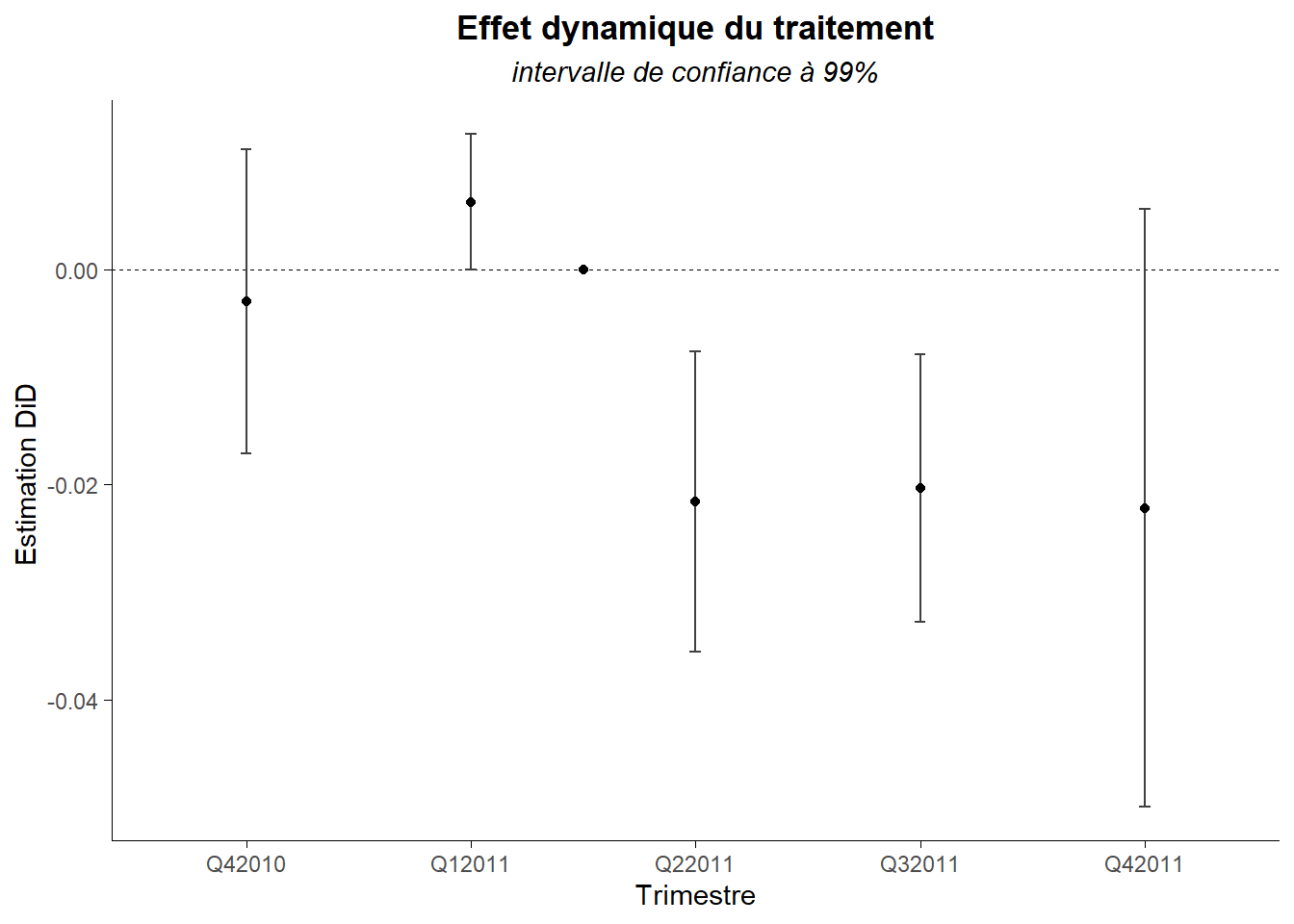
Ici, les choses sont plus nettes. Seuls les deux trimestres post traitement apparaissent statistiquement différents.