Laissons de côté les données de classement et revenons à des séries temporelles plus classiques. Ces séries sont généralement caractérisées de deux éléments structurant se cumulant avec la dimension aléatoire: une saisonnalité et une tendance de long terme. Si ces dimensions peuvent être observées sur les courbes des séries. Néanmoins, sauf cas particuliers où les choses sont fort marquées, le visuel classique trouve rapidement ses limites. Cela conduit généralement à travailler à partir de décomposition des séries en trois courbes (effet saisonnier, tendance, aléa). Le cycle graphe permet d’avoir une présentation plus simple et agrégée sur une seule figure. Il permet de montrer une tendance de long terme sur une série de segments de tendance saisonnière.
Commençons donc par charger le tidyverse et ggtext.
library(tidyverse)
library(ggtext)Travaillons une nouvelle fois à partir de données climatiques. Laissons un temps de coté les températures et tournons-nous vers les surfaces gelées en Arctique. Les données sont issues des travaux du NSIDC (National Snow and Ice Data Center). Nous avons chargé à partir du site Kaggle.com. Vous pouvez également les trouvez ici. L’unité de mesure est ici \(10^6km^2\) (Millions de \(km^2\)).
Chargeons-les dans notre dossier de travail. Puis, importons-les dans R.
seaice <- read_csv("seaice.csv")## Rows: 26354 Columns: 7
## ── Column specification ────────────────────────────────────────────────────────
## Delimiter: ","
## chr (2): Source Data, hemisphere
## dbl (5): Year, Month, Day, Extent, Missing
##
## ℹ Use `spec()` to retrieve the full column specification for this data.
## ℹ Specify the column types or set `show_col_types = FALSE` to quiet this message.Visualisons-les rapidement.
head(seaice)## # A tibble: 6 × 7
## Year Month Day Extent Missing `Source Data` hemis…¹
## <dbl> <dbl> <dbl> <dbl> <dbl> <chr> <chr>
## 1 1978 10 26 10.2 0 ['ftp://sidads.colorado.edu/pub/DATA… north
## 2 1978 10 28 10.4 0 ['ftp://sidads.colorado.edu/pub/DATA… north
## 3 1978 10 30 10.6 0 ['ftp://sidads.colorado.edu/pub/DATA… north
## 4 1978 11 1 10.7 0 ['ftp://sidads.colorado.edu/pub/DATA… north
## 5 1978 11 3 10.8 0 ['ftp://sidads.colorado.edu/pub/DATA… north
## 6 1978 11 5 11.0 0 ['ftp://sidads.colorado.edu/pub/DATA… north
## # … with abbreviated variable name ¹hemisphereIl y a pas mal de manipulations à faire pour rendre la base opérationnelle. Commençons par limiter la base à l’hémisphère Nord et de créons une variable unique indiquant les dates d’observations.
dat<-seaice %>%
filter(hemisphere=='north') %>%
mutate(date_=as.Date(paste0(as.character(Day),'/',
as.character(Month),'/',
as.character(Year)),
format='%d/%m/%Y')) %>%
select(date_,Extent) Voyons ce que l’on obtient.
head(dat)## # A tibble: 6 × 2
## date_ Extent
## <date> <dbl>
## 1 1978-10-26 10.2
## 2 1978-10-28 10.4
## 3 1978-10-30 10.6
## 4 1978-11-01 10.7
## 5 1978-11-03 10.8
## 6 1978-11-05 11.0Avant de réaliser notre cycle plot, explorons les données avec des graphes plus classique. Commençons par une simple courbe reprenant les relevés journaliers sur l’entièreté de la période d’observation.
ggplot(data=dat,aes(x=date_,y=Extent))+
geom_line()+
labs(title='Surface Gélée en Article',
subtitle ='(en millions de km<SUP>2</SUP> évolutions entre le 26/10/1978 et le 31/5/2019)',
caption='Source: NSIDC')+
coord_cartesian(expand=FALSE,ylim=c(2,18))+
theme_minimal()+
theme(
plot.title = element_text(hjust=0.5,face='bold'),
plot.subtitle = element_markdown(hjust=0.5,face='italic'),
plot.caption = element_text(hjust = 1,face='italic'),
axis.title = element_blank()
)
Deux éléments apparaissent comme marquant sur la série. Les vagues régulières sont le signe d’une saisonnalité dans les données. L’inclinaison générale de la courbe indique la présente d’un tendance baissière. Les surfaces gelées semblent diminuer. Néanmoins, concernant ce dernier point, les choses ne sont pas nettes sur la représentation.
Pour y voir plus clair sur cette tendance globale, on peut limiter la représentation aux seule moyenne annuelle. Celles-ci ne semble pas être affecté par par la saisonnalité. Pour cela, calculons ces moyennes.
dat_an<-dat %>% mutate(an=year(date_)) %>%
group_by(an) %>%
summarise(moy_a=mean(Extent))Utilisons un diagramme à bâtons pour illustrer la tendance.
ggplot(data=dat_an,aes(x=an,y=moy_a))+
geom_col()+
labs(title='Surface Gélée en Article',
subtitle ='(moyenne annuelles en millions de km<SUP>2</SUP> entre 1978-2019)',
caption='Source: NSIDC')+
theme_minimal()+
theme(
plot.title = element_text(hjust=0.5,face='bold'),
plot.subtitle = element_markdown(hjust=0.5,face='italic'),
plot.caption = element_text(hjust = 1,face='italic'),
axis.title = element_blank()
)
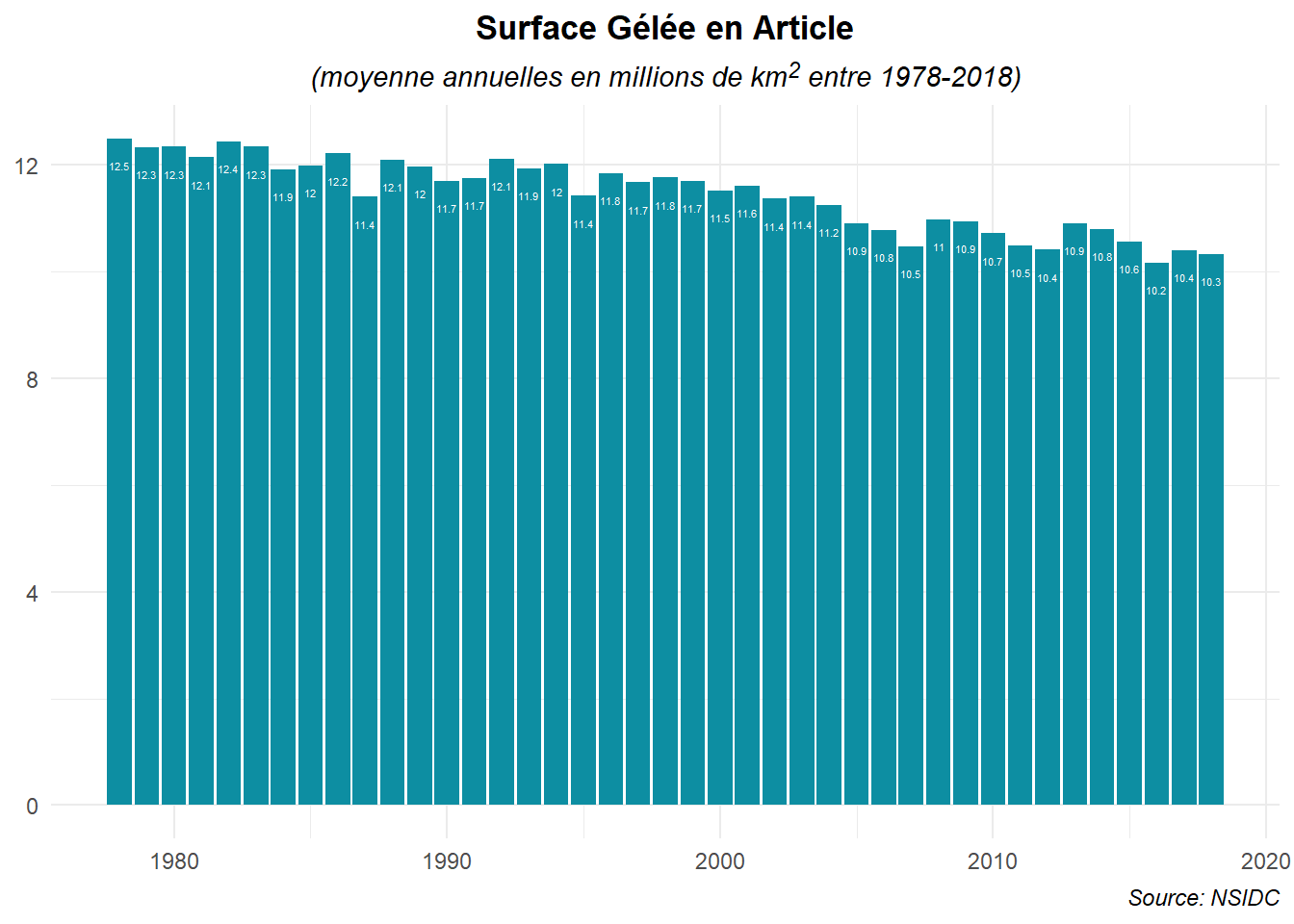
On voit bien que la surface gelée moyenne diminue sur la période avec une certaine régularité. Le pic constaté en 2019 est dû au fait que les mesures ne couvrent pas l’année entière (juste de janvier à mai). Il faut donc être prudent au sujet de cette observation tronquée. Il serait plus pertinent de l’ignorer. Profitons-en pour ajouter un peu de couleur et de texte.
ggplot(data=filter(dat_an,an!=2019),
aes(x=an,y=moy_a))+
geom_col(fill='#0D8EA2')+
geom_text(aes(label=round(moy_a,digits=1)),nudge_y = -0.5,
color='white',size=1.5)+
labs(title='Surface Gélée en Article',
subtitle ='(moyenne annuelles en millions de km<SUP>2</SUP> entre 1978-2018)',
caption='Source: NSIDC')+
theme_minimal()+
theme(
plot.title = element_text(hjust=0.5,face='bold'),
plot.subtitle = element_markdown(hjust=0.5,face='italic'),
plot.caption = element_text(hjust = 1,face='italic'),
axis.title = element_blank()
)
L’évolution est plus nette comme ça mais on perd la saisonnalité. Une autre solution qui met en évidence cette saisonnalité. Il s’agit d’établir une courbe par an établie sur chaque jour de l’année. Toutes les courbes sont alors inclues dans le même graphe avec une tinte différente. Ici, nous utiliserons des niveau de gris. Les plus sombres sont les plus récentes.
Préparons nos données en isolant les années et les jours au sein de ces années.
dat_an_<-dat %>% mutate(an=year(date_),
y_d=yday(date_)) %>%
filter(an!=1978 & an!=2019) Établissons le graphe. Pour notre dégradé de couleur, utilisons la fonction gray(). Celle-ci génère le code couleur d’un gris dont la nuance plus ou moins foncée est établie par le premier argument une valeur comprise entre 0 (gris clair) et 1 (gris foncé). Dans la mesure où nous avons 40 années de données, établissons une progression de 1/40ème.
ggplot(data=dat_an_,aes(x=y_d))+
geom_line(data=filter(dat_an_,an==1979),aes(y=Extent),color=gray(40/40))+
geom_line(data=filter(dat_an_,an==1980),aes(y=Extent),color=gray(39/40))+
geom_line(data=filter(dat_an_,an==1981),aes(y=Extent),color=gray(38/40))+
geom_line(data=filter(dat_an_,an==1982),aes(y=Extent),color=gray(37/40))+
geom_line(data=filter(dat_an_,an==1983),aes(y=Extent),color=gray(36/40))+
geom_line(data=filter(dat_an_,an==1984),aes(y=Extent),color=gray(35/40))+
geom_line(data=filter(dat_an_,an==1985),aes(y=Extent),color=gray(34/40))+
geom_line(data=filter(dat_an_,an==1986),aes(y=Extent),color=gray(33/40))+
geom_line(data=filter(dat_an_,an==1987),aes(y=Extent),color=gray(32/40))+
geom_line(data=filter(dat_an_,an==1988),aes(y=Extent),color=gray(31/40))+
geom_line(data=filter(dat_an_,an==1989),aes(y=Extent),color=gray(30/40))+
geom_line(data=filter(dat_an_,an==1990),aes(y=Extent),color=gray(29/40))+
geom_line(data=filter(dat_an_,an==1991),aes(y=Extent),color=gray(28/40))+
geom_line(data=filter(dat_an_,an==1992),aes(y=Extent),color=gray(27/40))+
geom_line(data=filter(dat_an_,an==1993),aes(y=Extent),color=gray(26/40))+
geom_line(data=filter(dat_an_,an==1994),aes(y=Extent),color=gray(25/40))+
geom_line(data=filter(dat_an_,an==1995),aes(y=Extent),color=gray(24/40))+
geom_line(data=filter(dat_an_,an==1996),aes(y=Extent),color=gray(23/40))+
geom_line(data=filter(dat_an_,an==1997),aes(y=Extent),color=gray(22/40))+
geom_line(data=filter(dat_an_,an==1998),aes(y=Extent),color=gray(21/40))+
geom_line(data=filter(dat_an_,an==1999),aes(y=Extent),color=gray(20/40))+
geom_line(data=filter(dat_an_,an==2000),aes(y=Extent),color=gray(19/40))+
geom_line(data=filter(dat_an_,an==2001),aes(y=Extent),color=gray(18/40))+
geom_line(data=filter(dat_an_,an==2002),aes(y=Extent),color=gray(17/40))+
geom_line(data=filter(dat_an_,an==2003),aes(y=Extent),color=gray(16/40))+
geom_line(data=filter(dat_an_,an==2004),aes(y=Extent),color=gray(15/40))+
geom_line(data=filter(dat_an_,an==2005),aes(y=Extent),color=gray(14/40))+
geom_line(data=filter(dat_an_,an==2006),aes(y=Extent),color=gray(13/40))+
geom_line(data=filter(dat_an_,an==2007),aes(y=Extent),color=gray(12/40))+
geom_line(data=filter(dat_an_,an==2008),aes(y=Extent),color=gray(11/40))+
geom_line(data=filter(dat_an_,an==2009),aes(y=Extent),color=gray(10/40))+
geom_line(data=filter(dat_an_,an==2010),aes(y=Extent),color=gray(9/40))+
geom_line(data=filter(dat_an_,an==2011),aes(y=Extent),color=gray(8/40))+
geom_line(data=filter(dat_an_,an==2012),aes(y=Extent),color=gray(7/40))+
geom_line(data=filter(dat_an_,an==2013),aes(y=Extent),color=gray(6/40))+
geom_line(data=filter(dat_an_,an==2014),aes(y=Extent),color=gray(5/40))+
geom_line(data=filter(dat_an_,an==2015),aes(y=Extent),color=gray(4/40))+
geom_line(data=filter(dat_an_,an==2016),aes(y=Extent),color=gray(3/40))+
geom_line(data=filter(dat_an_,an==2017),aes(y=Extent),color=gray(2/40))+
geom_line(data=filter(dat_an_,an==2018),aes(y=Extent),color=gray(1/40))+
labs(title='Surface Gélée en Article',
subtitle ="(en millions de km<SUP>2</SUP> évolutions sur l'année|1979-2018)",
caption='Source: NSIDC')+
scale_x_continuous(breaks=seq(0,365,15),
labels=c('','Jan.','','Fev.','','Mar.','','Avr.','',
'Mai','','Juin','','Juil.','','Aou.','',
'Sep.','','Oct.','','Nov.','','Dec.',''))+
theme_minimal()+
coord_cartesian(expand=FALSE)+
theme(
plot.title = element_text(hjust=0.5,face='bold'),
plot.subtitle = element_markdown(hjust=0.5,face='italic'),
plot.caption = element_text(hjust = 1,face='italic'),
axis.title = element_blank()
)
Le graphe obtenu marque bien la saisonnalité avec un pique de surface en février-Mars et un pique bas en Septembre. Par ailleurs, on note que les couleurs sombre se retrouvent en bas du ruban formé par les observations. Les années les plus récentes sont celles pour lesquelles les surfaces gelées sont les plus faibles.
La saisonnalité peut être mis en avant comme nous l’avons fait avec la tendance à partir d’un diagramme à bâtons illustrant les moyennes mensuelles.
dat_m<-dat %>%
mutate(mois=month(date_)) %>%
group_by(mois) %>%
summarise(moy_m=mean(Extent))Établissons le graphe en retenant les mêmes couleurs et textes.
ggplot(data=dat_m,aes(x=mois,y=moy_m))+
geom_col(fill='#3493A2')+
geom_text(aes(label=round(moy_m,digits=1)),nudge_y = -0.5,
color='white')+
labs(title='Surface Gélée en Article',
subtitle ="(en millions de km<SUP>2</SUP> moyenne sur chaque mois entre 1978 et 2019)",
caption='Source: NSIDC')+
coord_cartesian(expand=FALSE,ylim=c(0,17))+
theme_minimal()+
theme(
plot.title = element_text(hjust=0.5,face='bold'),
plot.subtitle = element_markdown(hjust=0.5,face='italic'),
plot.caption = element_text(hjust = 1,face='italic'),
axis.title = element_blank()
)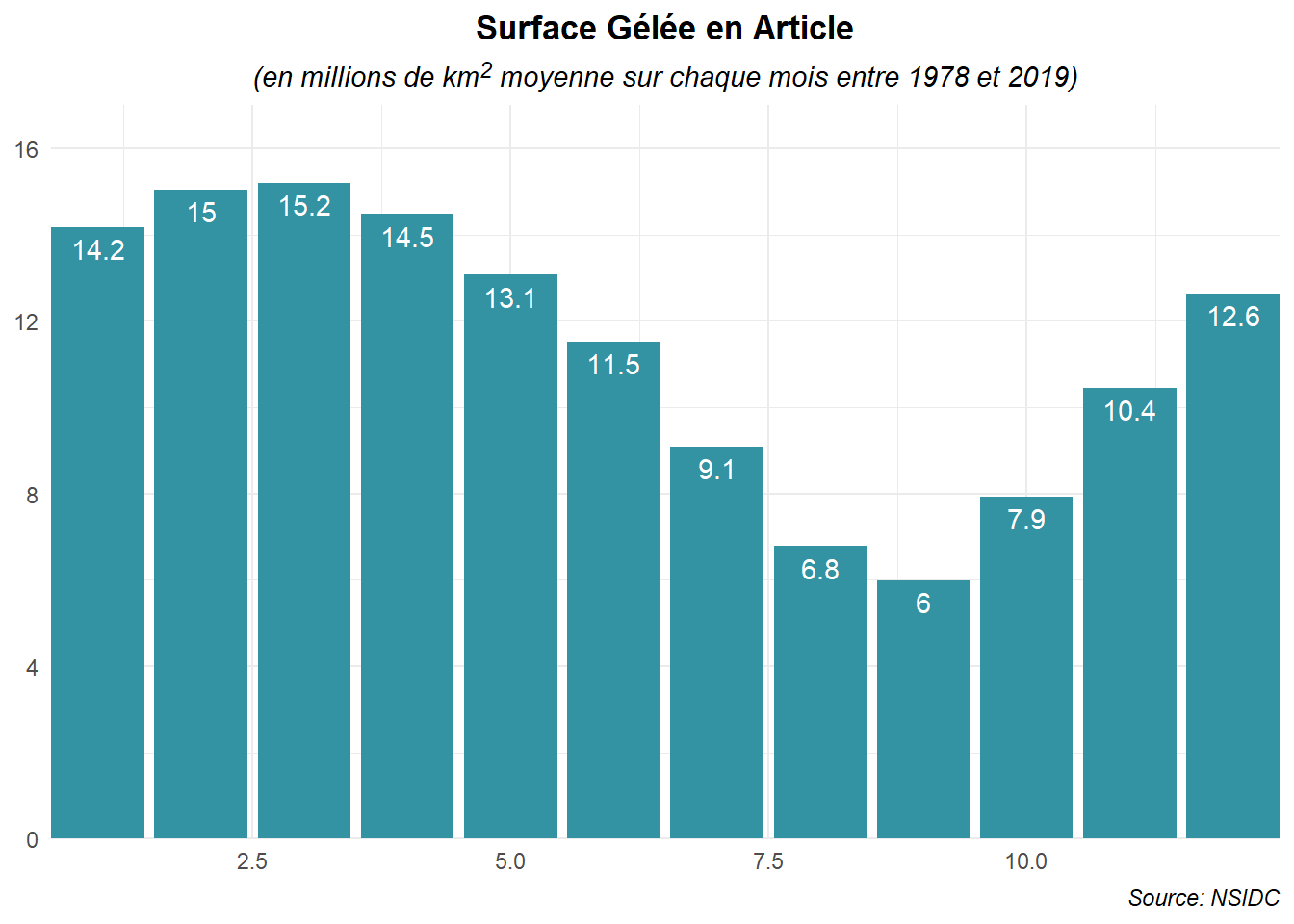
On retrouve les formes globales des courbes annuelles mais on perd l’évolution sur la période d’étude. Néanmoins, même avec les courbes annuelles, la tendance sur longue période était difficile à discerner.
Le cycle graphe permet d’illustrer clairement les deux éléments l’évolution saisonnière et la tendance de long terme.Préparons les données pour le réaliser. Isolons une variable indiquant le mois et calculons la moyenne des observations pour les différents mois.
dat_cyc<-dat %>%
mutate(mois=month(date_,label=TRUE)) %>%
group_by(mois) %>%
mutate(moy_m=mean(Extent))Traçons le graphe. On aura une facet par mois avec à l’intérieure une courbe pour les différentes valeurs de surface gelée et un droit horizontale marquant en rouge la moyenne du mois.
ggplot(data=dat_cyc,aes(x=date_,y=Extent))+
geom_line()+
geom_hline(aes(yintercept=moy_m),color='red')+
facet_grid(~ mois, switch = "x") +
theme_minimal()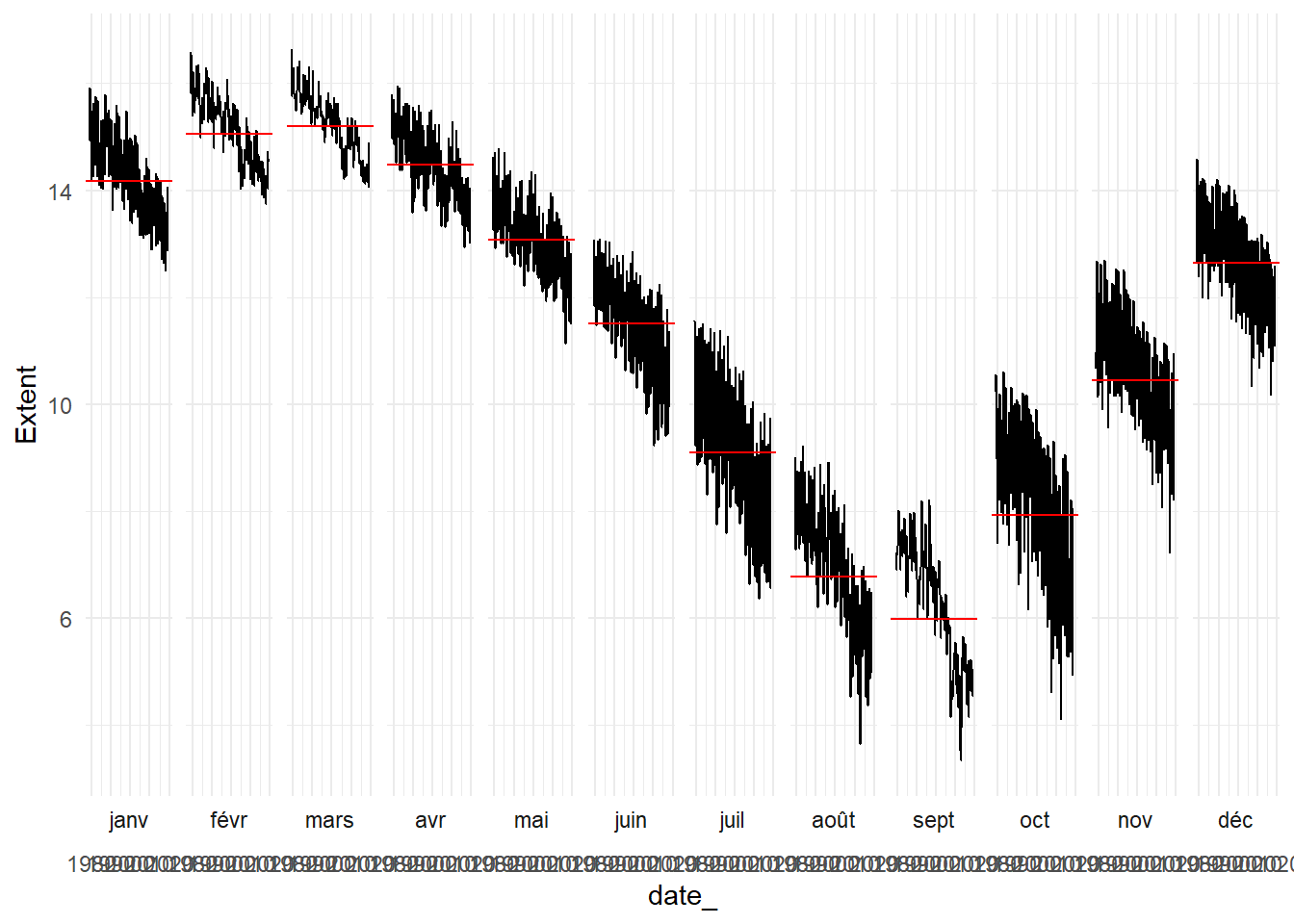
Le résultat nécessite en pas mal de travail pour être acceptable. Réduisons l’épaisseur de la courbe. Changeons la couleur. Modifions le fond du graphe ainsi que les annotations des axes. Ajoutons des éléments de texte (titre, sous-titre et caption).
ggplot(data=dat_cyc,aes(x=date_,y=Extent))+
geom_line(linewidth=0.2,color='#5996A0')+
geom_hline(aes(yintercept=moy_m),color='red')+
labs(title='Surface Gélée en Article',
subtitle ='(en millions de km<SUP>2</SUP> évolutions entre le 26/10/1978 et le 31/5/2019)',
caption='Source: NSIDC')+
facet_grid(~ mois, switch = "x") +
theme_minimal()+
theme(
plot.title = element_text(hjust=0.5,face='bold'),
plot.subtitle = element_markdown(hjust=0.5,face='italic'),
plot.caption = element_text(hjust = 1,face='italic'),
axis.title = element_blank(),
axis.text.x = element_blank(),
axis.line.x = element_line(colour='black'),
panel.grid = element_blank(),
panel.background = element_rect(fill='#E7E6E3',color='white')
)
Le résultat est bien meilleur. Le graphe permet bien de mettre en évidence la saisonnalité des données avec des niveaux différents mois par mois et la tendance générale à la baisse des valeurs avec la forme décroissante des courbes des observations au sein de ces mois. On voit bien que le maximum annuel est intervient en mars et le minimum en septembre et que les surfaces gelées indépendamment des mois de mesure baissent.
`