A l’occasion, il peut être utile de revenir sur des notions que l’on finit par utiliser sans réellement faire attention aux mécaniques impliqués. C’est le cas, notamment des estimateurs. Que ce soit les moindres carrés, des moindres carrés généralisés, ou encore le maximum de vraisemblance, nous les mobilisons parce que l’on sait qu’ils sont adéquates sans bien ce souvenir pourquoi. En tout cas, cela m’arrive. Aussi, je pense qu’il n’est jamais utile de réviser un petit peu les fondamentaux. C’est ce que propose cette série de postes qui commence avec le maximum de vraisemblance.
Chargeons le tidyverse pour procéder aux différentes manipulations de données illustratives et pour réaliser différents graphe via ggplot.
library(tidyverse)Vraisemblance et probabilité
Commençons par définir clairement ce que l’on entend pas vraisemblance. Faisons-le à partir d’une notion proche, celle de probabilité.
Pour cela, à titre d’illustration, considérons la mesure d’un phénomène pouvant être décrit par une variable aléatoire suivant une loi normale dont les paramètres sont les suivants: espérance mathématique 32 et écart-type 2,5. Générons les données associées sur l’intervalle 21-43.
esp<-32
et<-2.5
dat<-data.frame(x=seq(21,43,0.01),
y=dnorm(seq(21,43,0.01),mean=esp,sd=et))Traçons la courbe représentant la distribution de notre variable sur l’intervalle.
g1<-ggplot(data=dat,aes(x=x,y=y))+
geom_line(color='red',linewidth=1.5)+
scale_x_continuous(breaks=seq(24,40,2))+
coord_cartesian(expand=FALSE, ylim=c(-0.001,0.18))+
theme_minimal()+
theme(
axis.title = element_blank(),
axis.line = element_line(color='black'),
panel.grid = element_blank()
)
g1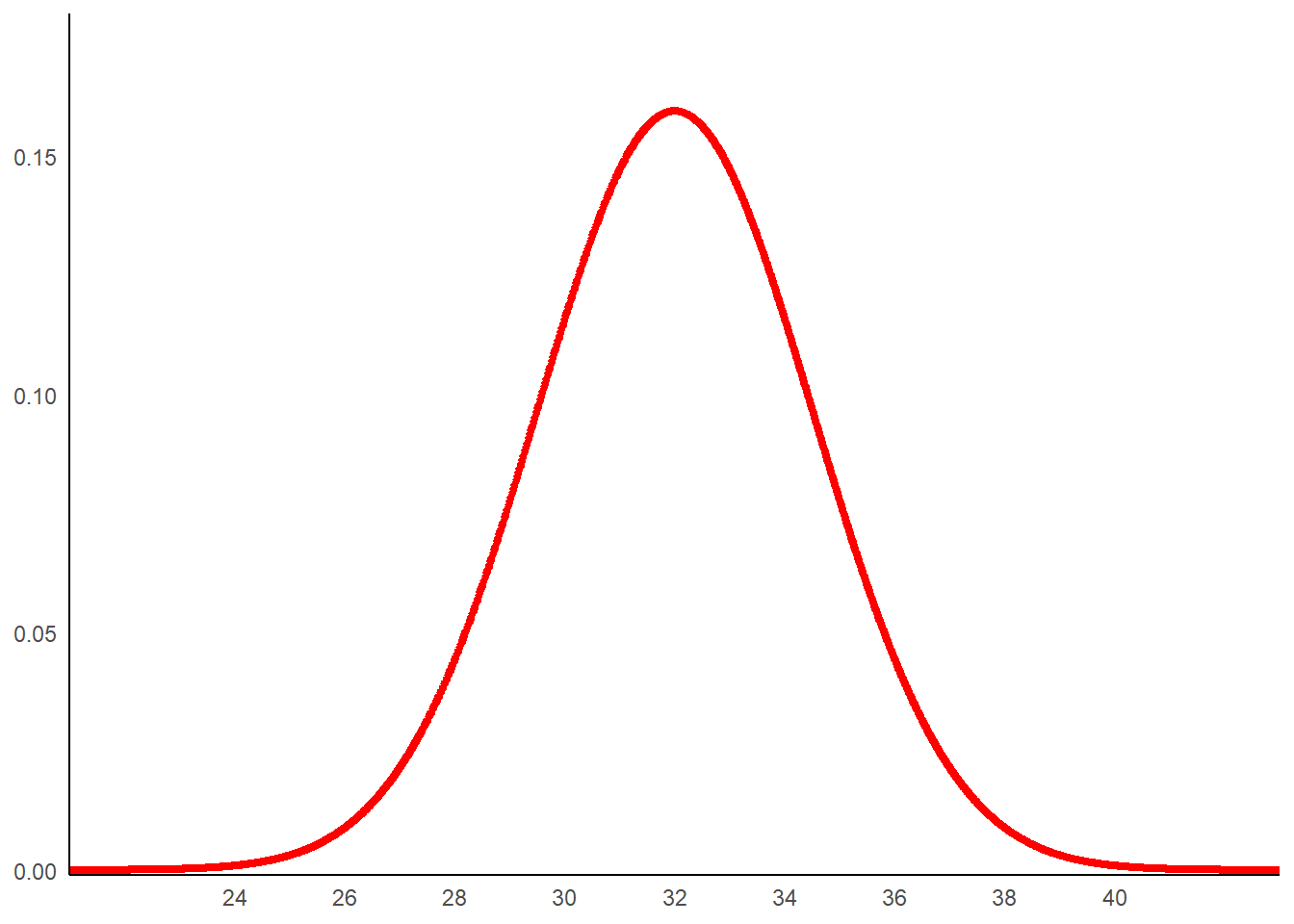
On retrouve bien la forme en cloche typique de la loi normale.
La probabilité d’un évènement données correspond à l’aire sous la courbe établie à partir des bornes définissant cet évènement (la loi est connu et donc ne connait pas de valeurs discrètes).
Prenons, par exemple, l’évènement: relever une valeur supérieure à 34. Pour en obtenir la probabilité, il faut mesurer l’aire sous la courbe entre 34 et plus infinie.
zone <- rbind(c(34,0), subset(dat, x > 34))
g1+
geom_polygon(data =zone , aes(x=x, y=y),fill="grey",alpha=0.5)+
geom_segment(aes(x = 34, y = 0, xend = 34, yend = dnorm(34,mean=32,sd=2.5)))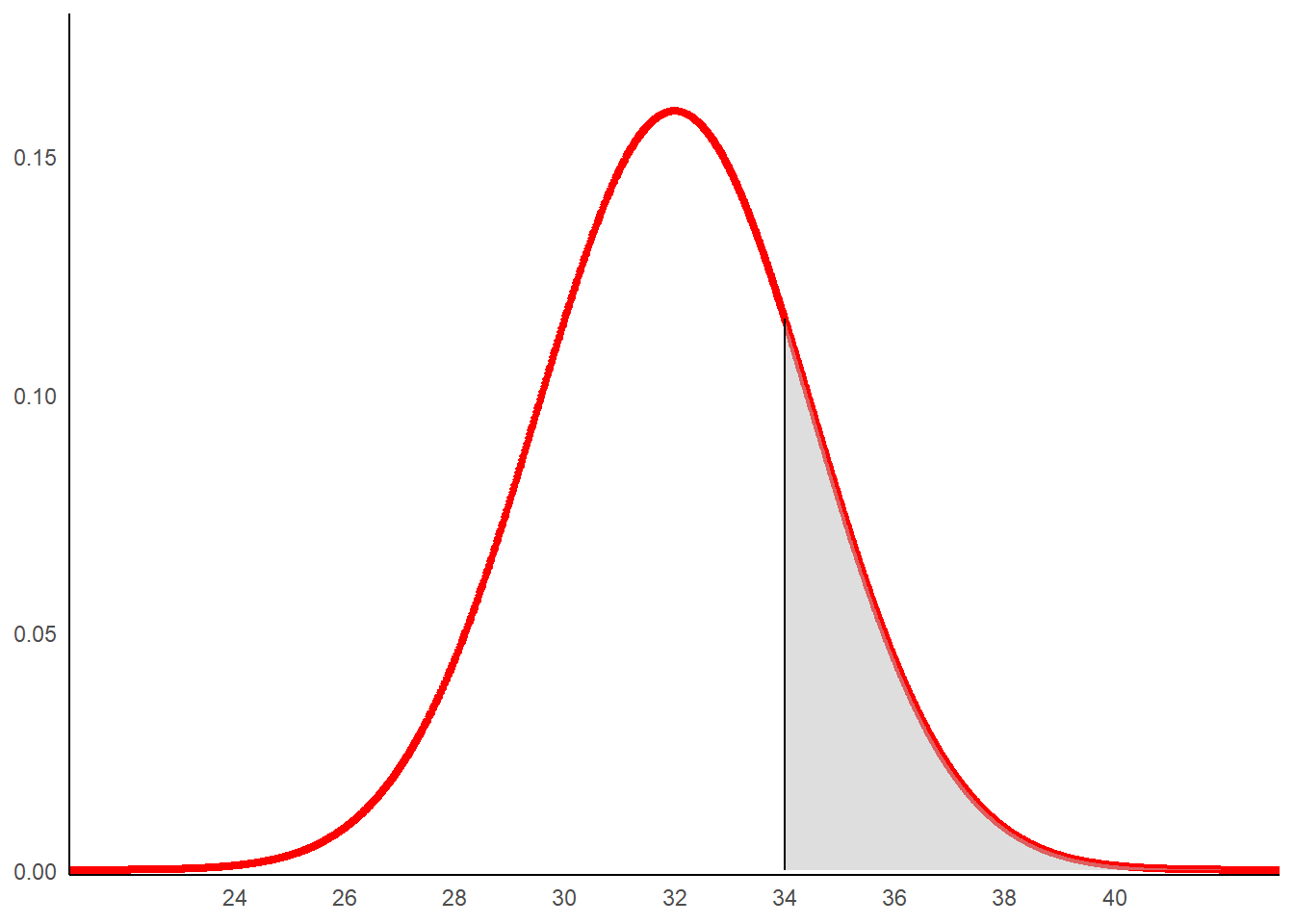
Cela revient à calculer l’intégrale suivante:
\[ \int^{+\infty}_{34}\frac{1}{\sigma\sqrt{2\pi}}e^{-\frac{1}{2}(\frac{x-\mu}{\sigma})^2} dx \]
\[ \int^{+\infty}_{34}\frac{1}{2,5\sqrt{2\pi}}e^{-\frac{1}{2}(\frac{x-32}{2,5})^2}dx \]
On peut néanmoins obtenir le résultat très rapidement avec la fonction pnorm() qui produit l’intégrale opposée (de moins l’infini à la valeur).
1-pnorm(34,mean=32,sd=2.5)## [1] 0.2118554Il y a ainsi un probabilité de 21% d’observer une mesure supérieure à 34 sachant que la loi de la variable est normale de paramètre (32;2,5). On a :
\[ P[x\geq34|N(32;2,5)]=21\% \]
Prenons un second exemple de calcule de probabilité. Considérons l’évènement: relever une valeur comprise entre 32 et 34.
zone_1 <- rbind(c(32,0), subset(dat, x > 32 & x<34),c(34,0))
g1+
geom_polygon(data =zone_1 , aes(x=x, y=y),fill="grey",alpha=0.5)+
geom_segment(aes(x = 32, y = 0, xend = 32, yend = dnorm(32,mean=32,sd=2.5)))+
geom_segment(aes(x = 34, y = 0, xend = 34, yend = dnorm(34,mean=32,sd=2.5)))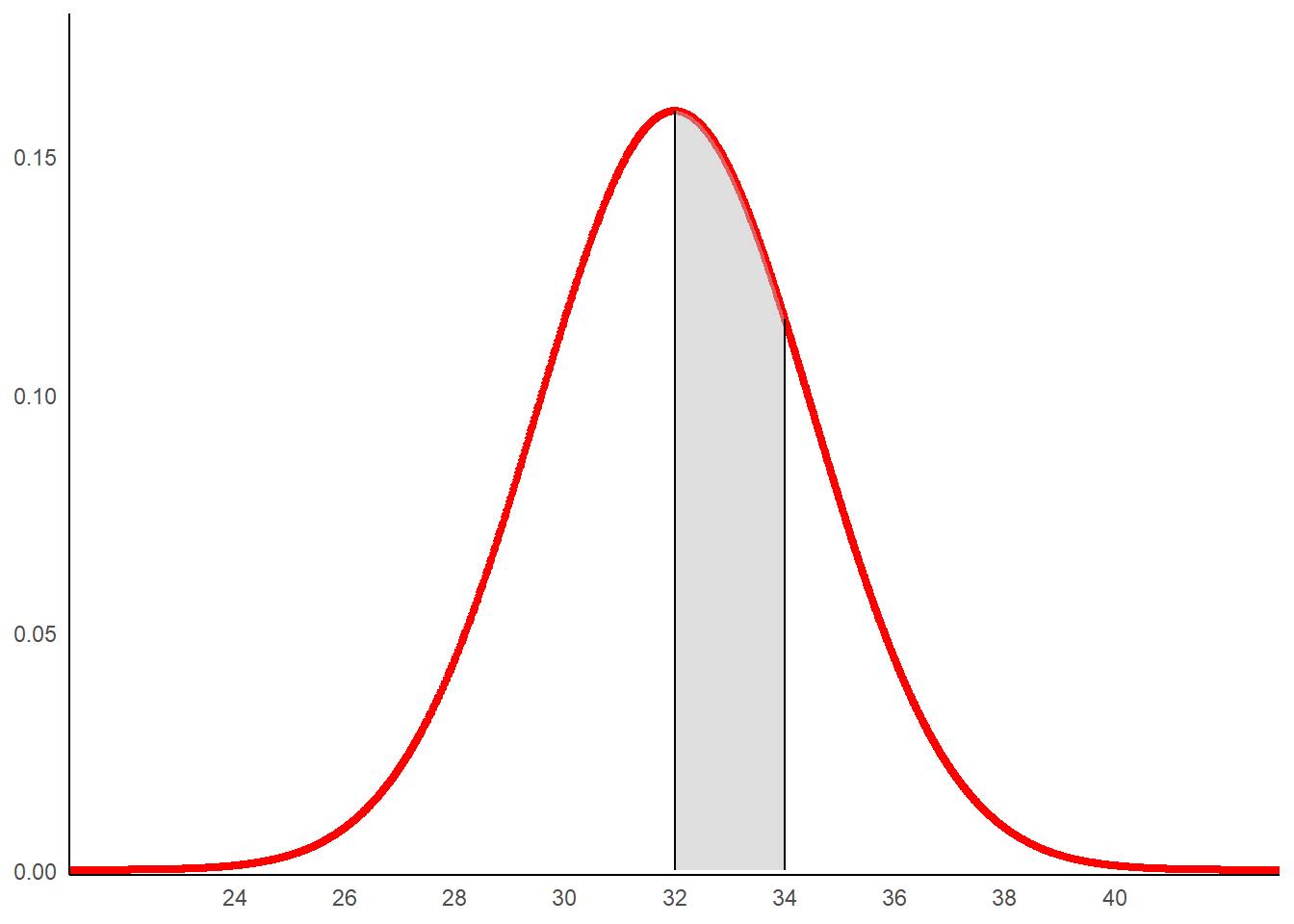
Cette fois l’intégrale à calculer est la suivante.
\[ \int^{34}_{32}\frac{1}{2,5\sqrt{2\pi}}e^{-\frac{1}{2}(\frac{x-32}{2,5})^2}dx \]
Encore une fois, on peut la calculer en utilisant pnorm().
round(pnorm(34,mean=32,sd=2.5)-pnorm(32,mean=32,sd=2.5),digits=2)## [1] 0.29Il y a ainsi un probabilité de 29% d’observer une mesure comprise entre 32 et 34 sachant que la loi de la variable est normale de paramètre (32;2,5). On a :
\[ P(32\geq x>34|N(32;2,5))=29\% \]
La probabilité d’un évènement est établi au sachant que la variable aléatoire décrivant le phénomène sous-jacent suit une loi connue (type de loi et paramètre).
\[ P[données|distribution] \]
La vraisemblance part du postulat opposée. Il s’agit de déterminer la probabilité que la loi décrivant la variable aléatoire soit celle suggérée sachant le ou les évènements constaté (les données recueillies).
\[ L(distribution|données) \]
Illustrons cela à partir d’un exemple. Admettons que l’on ait relevé une valeur de 34. Si la loi sous-jacent dans laquelle le tirage qui a permis d’obtenir cette mesure est une loi normale d’espérance 32 et d’écart-type 2,5, la vraisemblance de ce résultat correspond au point de la distribution associé à la valeur 34. On a:
g1+
geom_point(aes(x=34,y=0),size=3,color='blue')+
geom_point(aes(x=34,y=dnorm(34,mean=32,sd=2.5)),size=3,color='blue')+
geom_point(aes(x=21,y=dnorm(34,mean=32,sd=2.5)),size=3,color='blue')+
geom_segment(aes(x=34,y=0,xend=34,yend=dnorm(34,mean=32,sd=2.5)),
color='blue',linetype='dashed')+
geom_segment(aes(x=34,y=dnorm(34,mean=32,sd=2.5),
xend=21,yend=dnorm(34,mean=32,sd=2.5)),
color='blue',linetype='dashed')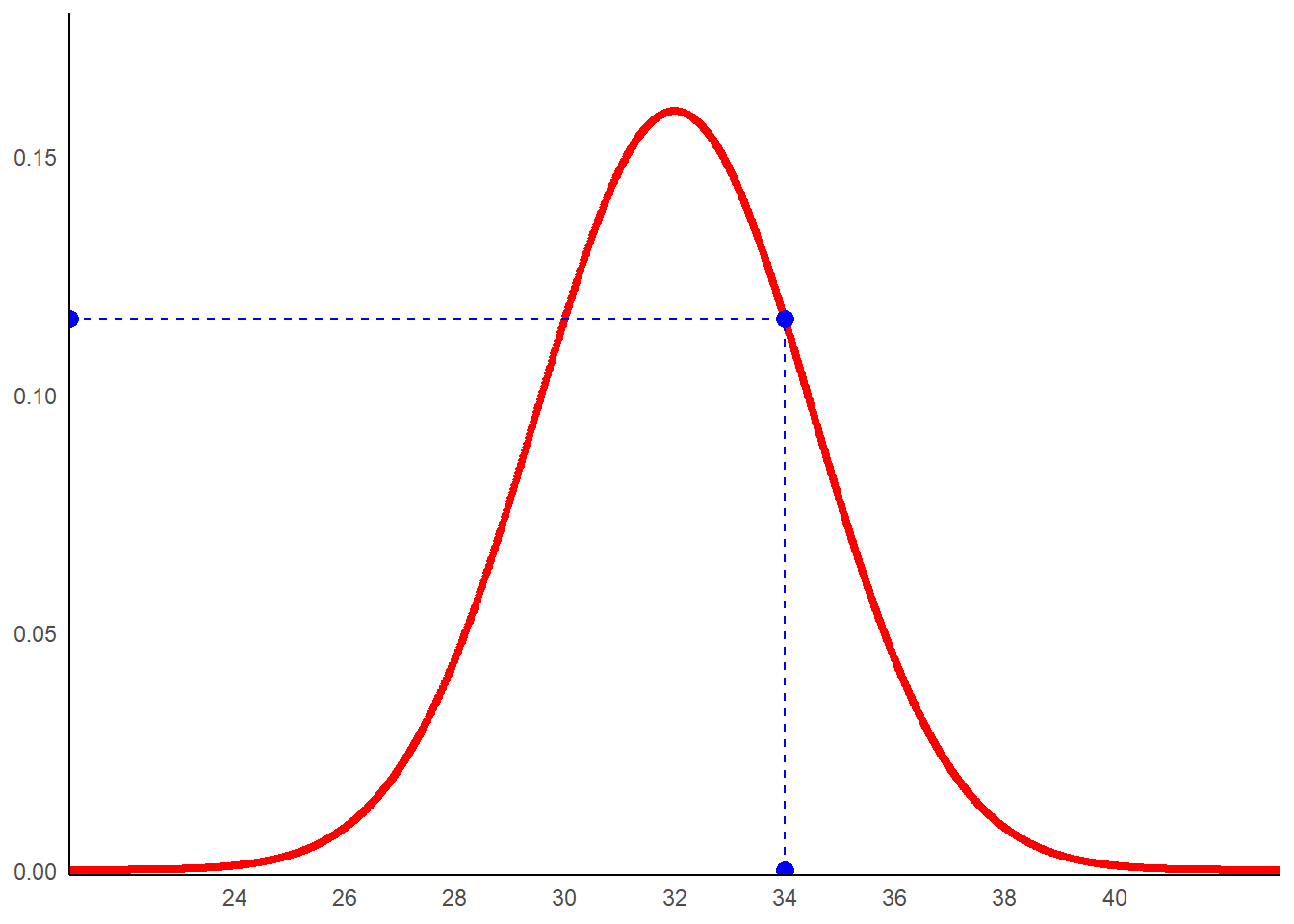
La vraisemblance est obtenue en incluant dans la valeur observée dans la formule de la distribution normale dont on connait la distribution.
\[ L[N(32;2,5)|x=34]=\frac{1}{2,5\sqrt{2\pi}}e^{-\frac{1}{2}(\frac{34-32}{2,5})^2} \]
Calculons cette valeur en utilisant R comme une calculatrice.
1/(2.5*sqrt(2*pi))*exp(-0.5*((34-32)/2.5)^2)## [1] 0.1158766Une autre possibilité est d’utiliser la fonction dnorm().
dnorm(34,mean=32,sd=2.5)## [1] 0.1158766La vraisemblance du fait que la loi (non observée) dans laquelle le tirage a été réalisé est bien une loi normal de paramètres 32 et 2,5 sachant que ce même tirage a donné 34 est de 12%.
\[ L(N(32;2,5)|x=34)=P(N(32;2,5)|x=34)=12\% \]
Considérons un nouvel exemple. La même mesure est réalisée (34) mais cette fois on pense que le tirage a été réalisé dans une loi normale d’espérance 34 et d’écart-type de 2,5. Calculons la vraisemblance de cette supposition.
Mais avant d’aller plus loin, visualisons la chose.
esp<-34
et<-2.5
dat2<-data.frame(x=seq(25,43,0.01),
y=dnorm(seq(25,43,0.01),mean=esp,sd=et))
ggplot(data=dat2,aes(x=x,y=y))+
geom_line(color='red',linewidth=1.5)+
geom_point(aes(x=34,y=0),size=3,color='blue')+
geom_point(aes(x=34,y=dnorm(34,mean=34,sd=2.5)),size=3,color='blue')+
geom_point(aes(x=25,y=dnorm(34,mean=34,sd=2.5)),size=3,color='blue')+
geom_segment(aes(x=34,y=0,xend=34,yend=dnorm(34,mean=34,sd=2.5)),
color='blue',linetype='dashed')+
geom_segment(aes(x=34,y=dnorm(34,mean=34,sd=2.5),
xend=25,yend=dnorm(34,mean=34,sd=2.5)),
color='blue',linetype='dashed')+
scale_x_continuous(breaks=seq(26,40,2))+
coord_cartesian(expand=FALSE, ylim=c(-0.001,0.18))+
theme_minimal()+
theme(
axis.title = element_blank(),
axis.line = element_line(color='black'),
panel.grid = element_blank()
)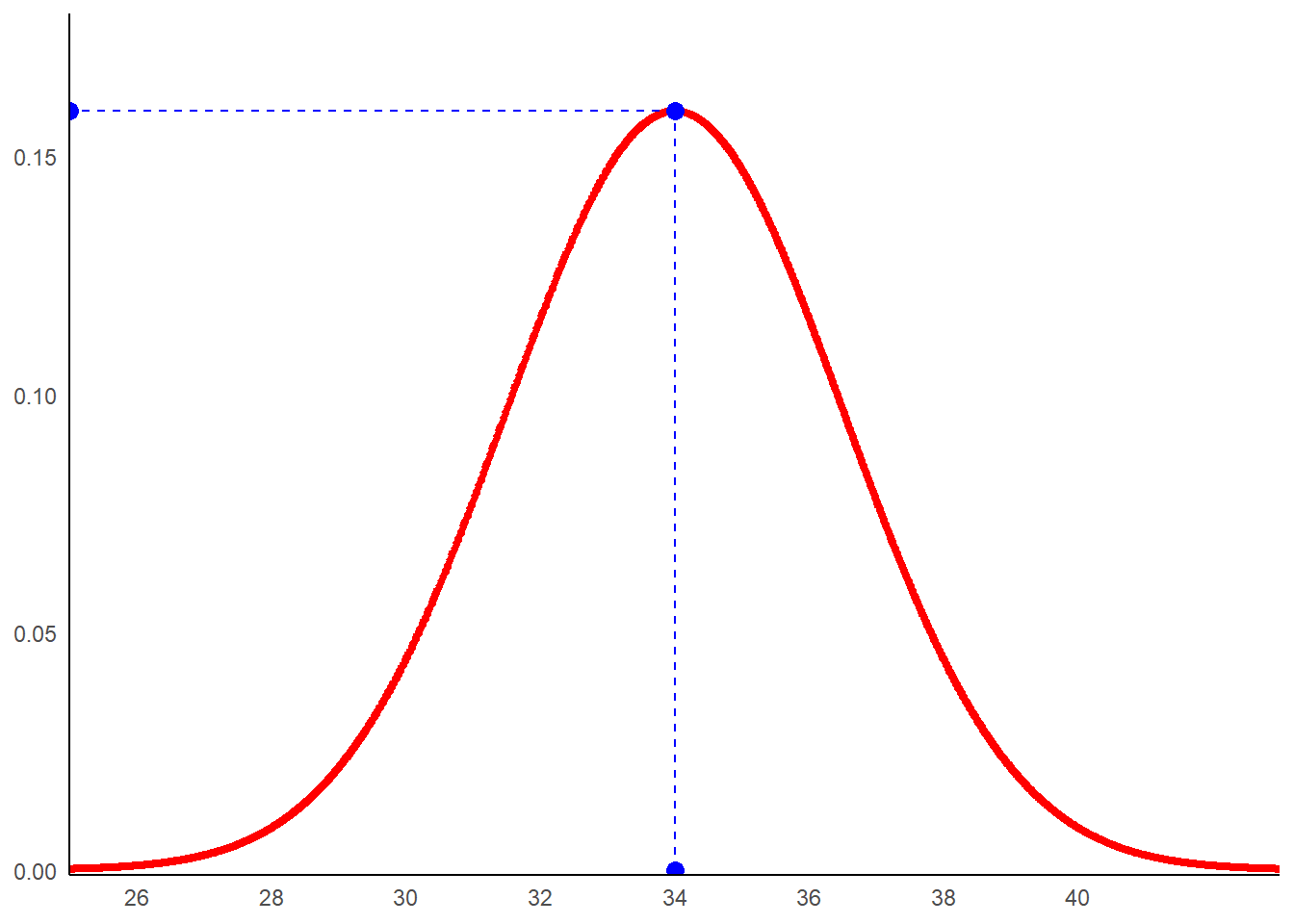
La vraisemblance est obtenue en incluant dans la valeur observée dans la formule de la distribution normale dont on connait la distribution.
\[ L[N(34;2,5)|x=34]=\frac{1}{2,5\sqrt{2\pi}}e^{-\frac{1}{2}(\frac{34-34}{2,5})^2} \]
Calculons cette valeur en utilisant R comme une calculatrice.
1/(2.5*sqrt(2*pi))*exp(-0.5*((34-34)/2.5)^2)## [1] 0.1595769Une autre possibilité est d’utiliser la fonction dnorm().
dnorm(34,mean=34,sd=2.5)## [1] 0.1595769La vraisemblance du fait que la loi (non observée) dans laquelle le tirage a été réalisé est bien une loi normal de paramètres 32 et 2,5 sachant que ce même tirage a donné 34 est de 16%.
\[ L(N(34;2,5)|x=34)=P(N(34;2,5)|x=34)=16\% \]
Notez que la vraisemblance est plus élevée ici quand l’espérance de la loi normale sous-jacente correspond à l’observation.
L’estimateur Maximum de vraisemblance
Plus la vraisemblance est importante, plus la probabilité que la loi sous-jacente dont nous supposons connaître les paramètres soit celles dans laquelle les tirages produisant les données ont été réalisé est importante.
Sachant cela, et connaissant la forme globale de cette loi, on peut rechercher à partir des données observées la valeur des paramètres qui permettent d’obtenir la plus grande valeur de vraisemblance.
C’est le principe de l’estimateur du maximum de vraisemblance.
La procédure consiste alors à établir la fonction de vraisemblance, à la dériver, puis à chercher les valeurs des paramètres permettant d’annuler cette dérivée.
Maximum de vraisemblance pour une distribution exponentielle
Pour illustrer le propos, considérons une loi avec un seul paramètre. Utilisons la loi exponentielle. Celle-ci est mobilisée pour modéliser la durée de vie d’un phénomène dont la probabilité de cesser n’est pas dépendant du temps écoulé. Sa fonction de densité prend la forme suivante:
\[ f(x)=\lambda.e^{-\lambda x} \]
Elle n’a qu’un paramètre que l’on nomme lambda (\(\lambda\)).
Prenons lamba égale 1 et générons des données.
lamb<-1
dat_exp<-data.frame(x=seq(0,10,0.01),
y=dexp(seq(0,10,0.01),rate=lamb))Traçons la fonction de répartition pour cette valeur de paramètre.
g_exp<-ggplot(data=dat_exp,aes(x=x,y=y))+
geom_line(color='red',linewidth=1.5)+
scale_x_continuous(breaks=seq(0,10,1))+
coord_cartesian(expand=FALSE, ylim=c(-0.001,1))+
theme_minimal()+
theme(
axis.title = element_blank(),
axis.line = element_line(color='black'),
panel.grid = element_blank()
)
g_exp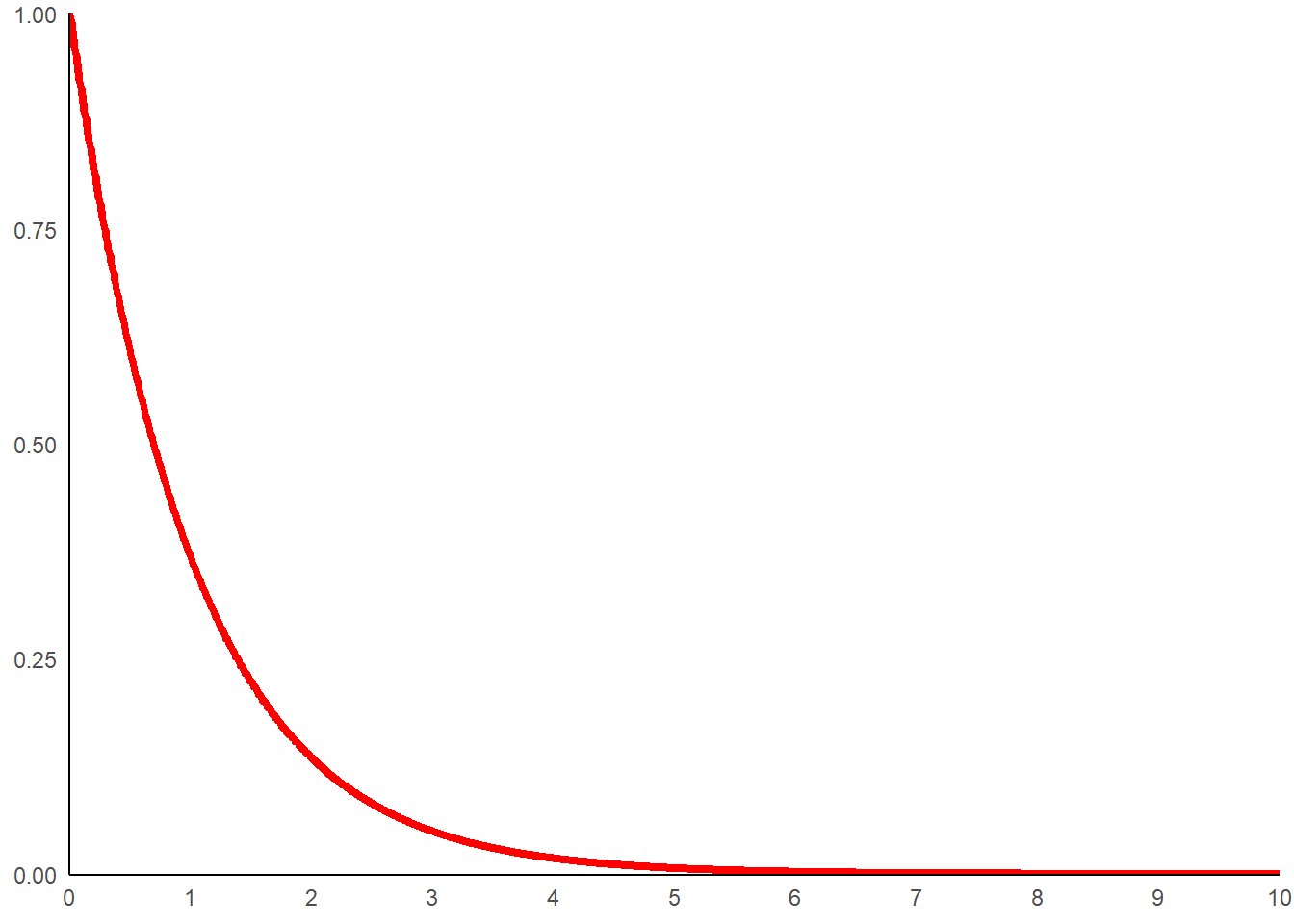
Les unités en abscisse (x) correspondent à du temps écoulé. La probabilité que la durée écoulé avant l’évènement soit 2 correspond à l’aire sous la courbe comprise entre 0 et 2.
Voyons comment la courbe varie en fonction de lambda. Ajoutons une courbe avec lambda 2 et une avec lambda 0.
dat_exp_2<-data.frame(x=seq(0,10,0.01),
y=dexp(seq(0,10,0.01),rate=2))
dat_exp_05<-data.frame(x=seq(0,10,0.01),
y=dexp(seq(0,10,0.01),rate=0.5))
g_exp+
geom_line(data= dat_exp_2,aes(x=x,y=y),color='blue',linewidth=1)+
geom_line(data= dat_exp_05,aes(x=x,y=y),color='purple',linewidth=1)+
coord_cartesian(expand=FALSE, ylim=c(-0.001,2.1))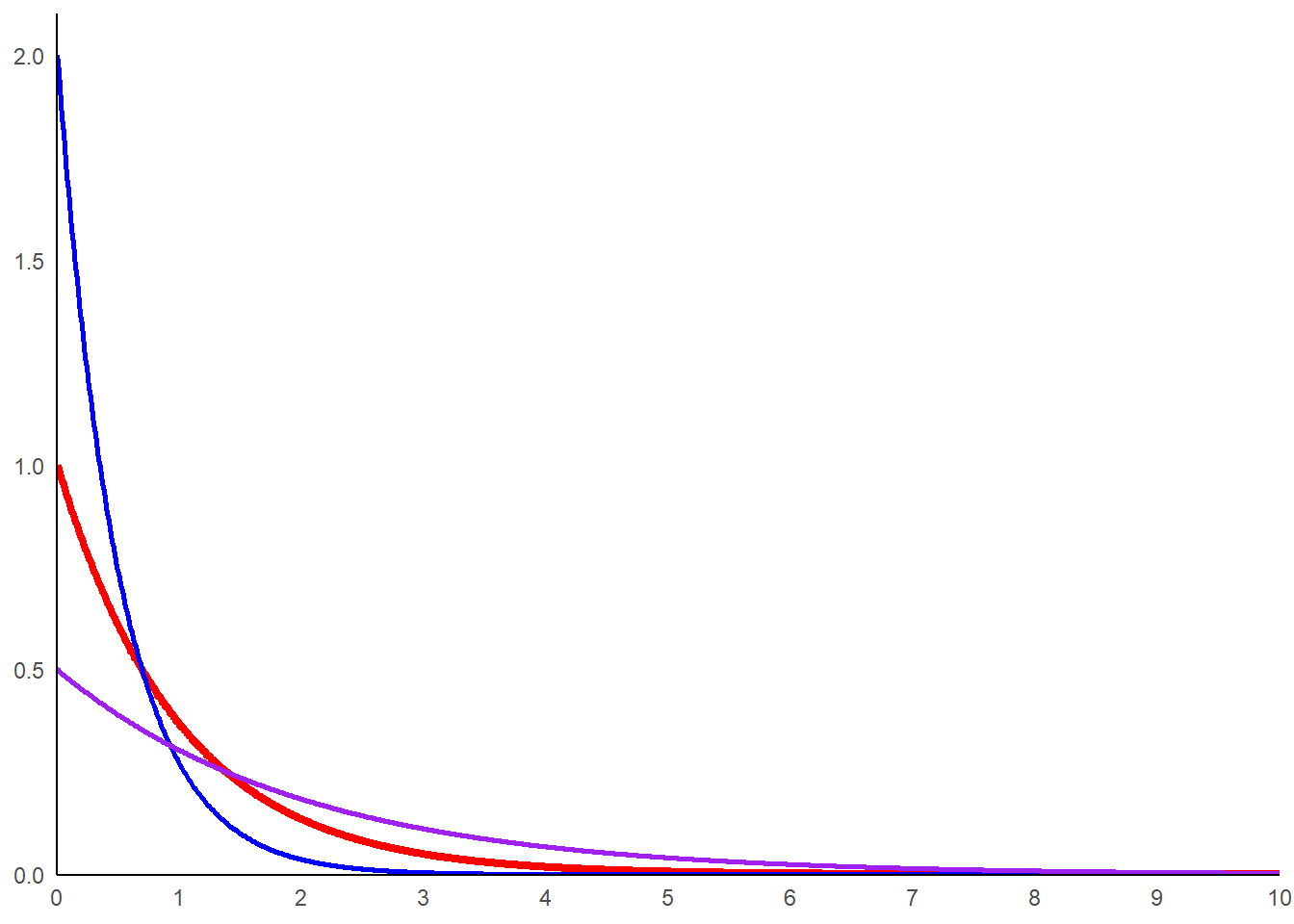
La vraisemblance du paramètre Lambda compte tenu du fait d’avoir observé que l’évènement s’est produit suite à la durée \(x_1\) est :
\[ L(\lambda|x_1)y=\lambda e^{-\lambda x_1} \]
La vraisemblance du paramètre Lambda compte tenu du fait d’avoir observé que l’évènement s’est produit suite à la durée \(x_2\) est :
\[ L(\lambda|x_2)y=\lambda e^{-\lambda x_2} \]
La vraisemblance de lambda et les deux évènements interviennent après des durées \(x_1\) et \(x_2\) est, compte tenu du fait que les évènements sont indépendant, la suivante:
\[ L(\lambda| x_1 \& x_2) = L(\lambda| x_1 ) L(\lambda| x_2)=\lambda e^{-\lambda x_1} \lambda e^{-\lambda x_2} \]
\[ L(\lambda| x_1 \& x_2) = \lambda^2 (e^{-\lambda x_1} e^{-\lambda x_2})=\lambda^2 [e^{-\lambda (x_1+x_2)}] \]
\[ L(\lambda| x_1 \& x_2) = \lambda^2 [e^{-\lambda (x_1+x_2)}] \]
Etendons l’expression au cas où n évènements ont été constatés.
\[ L(\lambda|x_1,x_2,...,x_n)=\lambda^n [e^{-\lambda (x_1+x_2+...+x_n)}] \]
Il s’agit alors, pour déterminer la valeur la plus adéquate de lambda, de maximiser cette fonction en faisant varier ce paramètre.
Pour ce faire, commençons par dériver la fonction de vraisemblance de manière à travers la valeur de lambda qui permet d’égaliser cette dérivée à 0. On a:
\[ \frac{\delta }{\delta \lambda}L(\lambda|x_1,x_2,...,x_n)=0 \]
\[ \frac{\delta }{\delta \lambda}(\lambda^n [e^{-\lambda (x_1+x_2+...+x_n)}])=0 \]
Il est plus facile ici de travailler à partir de la log vraisemblance (celle-ci ici donne la même valeur max pour le paramètre).
\[ \frac{\delta }{\delta \lambda}(ln(\lambda^n [e^{-\lambda (x_1+x_2+...+x_n)}]))=0 \]
\[ \frac{\delta }{\delta \lambda}(ln(\lambda^n)+ln[e^{-\lambda (x_1+x_2+...+x_n)}])=0 \]
\[ \frac{\delta }{\delta \lambda}(n.ln(\lambda)-\lambda (x_1+x_2+...+x_n))=0 \]
Dérivons par lambda et résolvons l’équation.
\[ n.\frac{1}{\lambda}-(x_1+x_2+...+x_n)=0 \]
\[ \frac{n}{\lambda}=x_1+x_2+...+x_n \]
\[ n=(x_1+x_2+...+x_n).\lambda \]
\[ \lambda=\frac{n}{x_1+x_2+...+x_n} \]
La valeur du paramètre lambda qui permet de maximiser correspond au nombre des observations (des évènements) divisé par la somme des valeurs de x observées (les durées écoulés avant les évènements).
Prenons un exemple chiffré de l’application de cette méthode. On constate que des évènements interviennent respectivement à \(x_1=2\), \(x_2=2.5\) et \(x_3=1.5\). Le lambda estimé par le maximum de vraisemblance (ML) est :
\[ \lambda=\frac{3}{2+2.5+1.5}=\frac{3}{6}=0.5 \]
Générons les données correspondant pour la loi exponentiel de paramètre lambda de 0.5.
lamb<-0.5
dat_exp<-data.frame(x=seq(0,10,0.01),
y=dexp(seq(0,10,0.01),rate=lamb))Observons cela au travers d’un graphe en y reportant les points valeurs observées.
ggplot(data=dat_exp,aes(x=x,y=y))+
geom_line(color='red',linewidth=1.5)+
geom_point(aes(x=2,y=dexp(2,rate=lamb)),size=3,color='blue')+
geom_segment(aes(x=2,y=0,xend=2,yend=dexp(2,rate=lamb)),
color='blue',linetype='dashed')+
geom_segment(aes(x=2,y=dexp(2,rate=lamb),
xend=0,yend=dexp(2,rate=lamb)),
color='blue',linetype='dashed')+
geom_point(aes(x=2.5,y=dexp(2.5,rate=lamb)),size=3,color='blue')+
geom_segment(aes(x=2.5,y=0,xend=2.5,yend=dexp(2.5,rate=lamb)),
color='blue',linetype='dashed')+
geom_segment(aes(x=2.5,y=dexp(2.5,rate=lamb),
xend=0,yend=dexp(2.5,rate=lamb)),
color='blue',linetype='dashed')+
geom_point(aes(x=1.5,y=dexp(1.5,rate=lamb)),size=3,color='blue')+
geom_segment(aes(x=1.5,y=0,xend=1.5,yend=dexp(1.5,rate=lamb)),
color='blue',linetype='dashed')+
geom_segment(aes(x=1.5,y=dexp(1.5,rate=lamb),
xend=0,yend=dexp(1.5,rate=lamb)),
color='blue',linetype='dashed')+
scale_x_continuous(breaks=seq(0,10,1))+
coord_cartesian(expand=FALSE, ylim=c(-0.001,0.6))+
theme_minimal()+
theme(
axis.title = element_blank(),
axis.line = element_line(color='black'),
panel.grid = element_blank()
)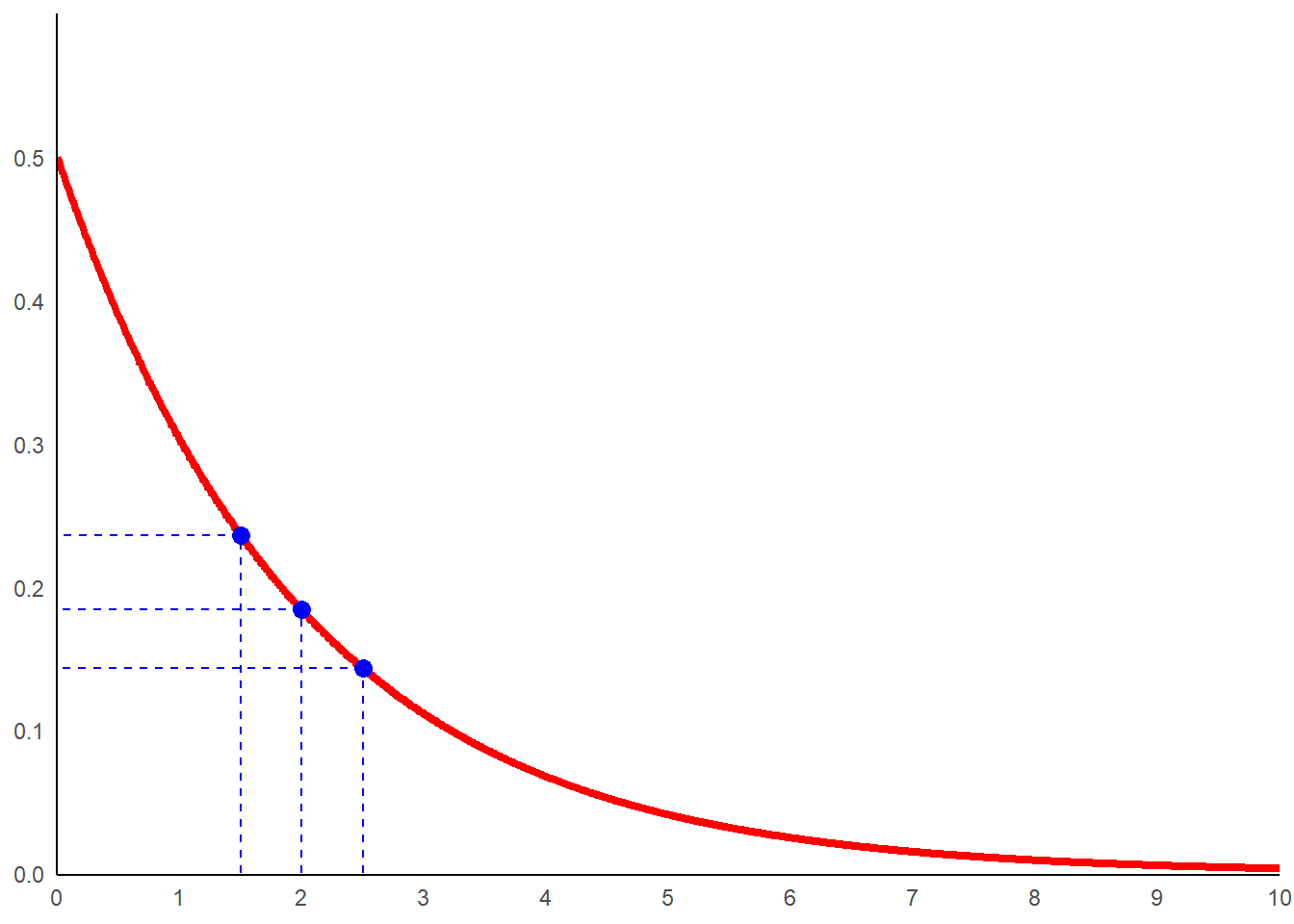
Cette courbe correspond à celle présentant la plus grande vraisemblance compte tenu des données observées.
Maximum de vraisemblance pour une distribution binomiale
Prenons un second exemple de loi à un seul paramètre. Cette fois travaillons sur une loi discrète. Considérons une variable aléatoire suivant une loi binomiale. Celle-ci décrit un phénomène correspondant au nombre de fois (x) où un résultat défini est obtenu suite à un nombre défini d’expériences aléatoires (n). Sa fonction de densité est la suivante:
\[ f(x|n)=\frac{n!}{x!(n-x)!}p^x.(1-p)^{n-x} \]
Elle n’a qu’un paramètre: p. Il s’agit de probabilité qu’un évènement soit un succès.
Prenons un exemple. On a conduit 7 expériences et 4 d’entre elles sont des réussites. Calculons la probabilité de ce résultat si la probabilité de réussite de chaque expérience (p) est de 50%.
On a ainsi par exemple:
\[ P(x=4;n=7|p=0,5)=\frac{7!}{4!(7-4)!}0,5^4.(1-0,5)^{7-4} \]
Ce qui nous donne, si on détail le calcul.
\[ P(x=4;n=7|p=0,5)=\frac{5040}{144}\times0,0625\times0,125=0.273 \]
La même résultat peut être obtenu avec R .
(factorial(7)/(factorial(4)*factorial(7-4)))*0.5^4*(1-0.5)^(7-4)## [1] 0.2734375Le même résultat peut être obtenu en utilisant la fonction dbinom().
dbinom(4,size=7,prob=0.5)## [1] 0.2734375Pour les distributions discrètes, la vraisemblance est la probabilité se confonde. On a :
\[ L(p|(n;x))=P((n;x)|p) \]
Ainsi, la vraisemblance de la distribution binomiale est donc:
\[ L(p|(n;x))=\frac{n!}{x!(n-x)!}p^x.(1-p)^{n-x} \]
Calculons la pour une valeur du paramètre p de 50% sachant que sur 7 expériences 4 ont produit un résultat positif.
\[ L(p=0,5|(n=7;x=4))=\frac{7!}{4!(7-4)!}0,5^4.(1-0,5)^{7-4}=0,273 \]
La vraisemblance de ce paramètre compte tenu des données est de 27,3%, ce qui correspond à la probabilité de constaté 4 réussites sur 7 essais sachant que le taux de succès est de 50% (probabilité que l’on vient de calculer).
Mais qu’elle est la valeur du paramètre que permet de maximiser la vraisemblance?
Pour s’en donner une idée, représentant dans un graphe la fonction de vraisemblance de notre distribution binomiale pour diférentes valeur du paramètre p.
dat<-data.frame(p=seq(0,1,0.01),
L=dbinom(4,7,prob=seq(0,1,0.01)))
ggplot(data=dat,aes(x=p,y=L))+
geom_line(color='red',linewidth=1)+
labs(y="Vraisemblance")+
coord_cartesian(expand=FALSE,ylim=c(0,0.35))+
theme_minimal()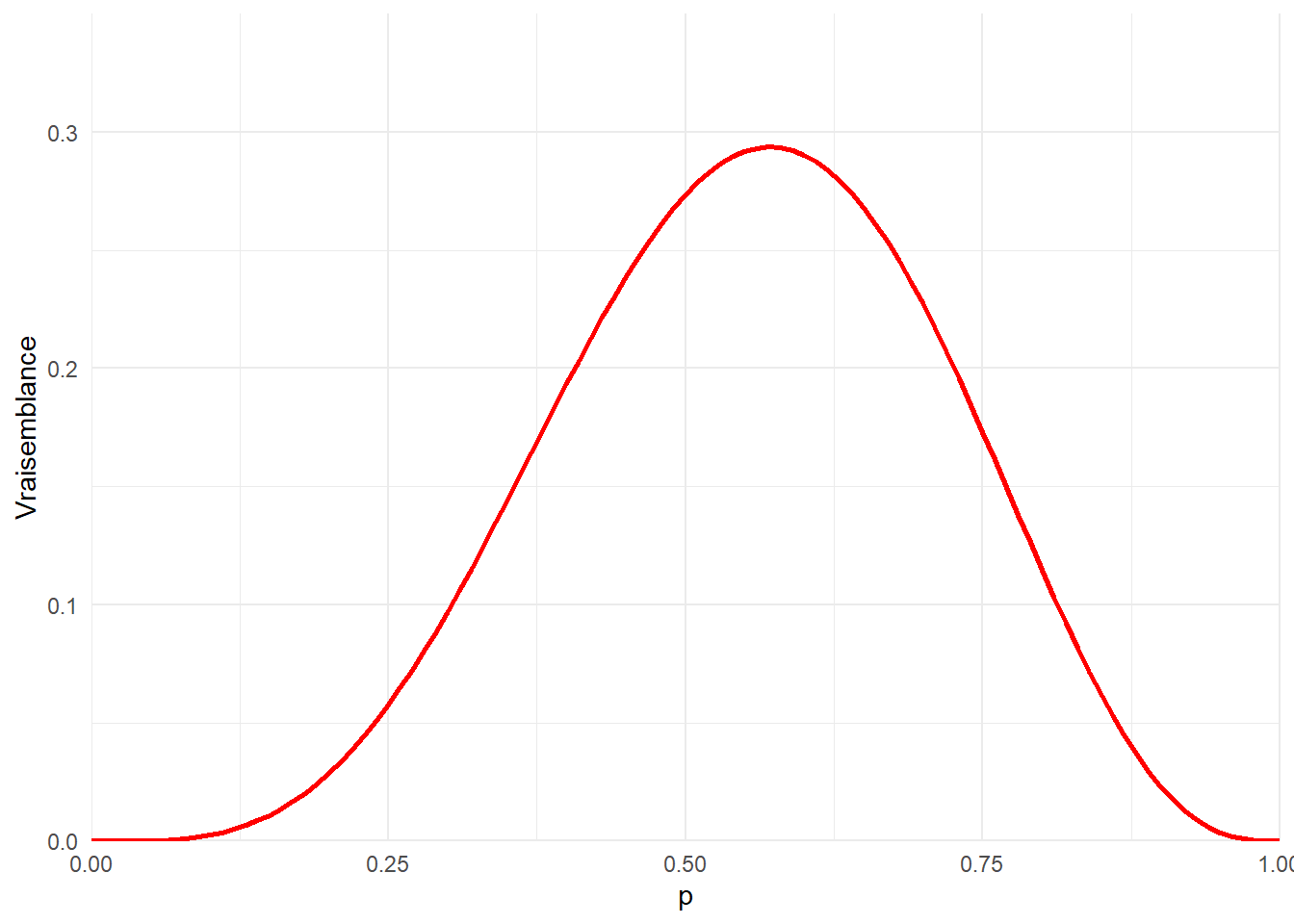
On a bien un maximum. Calculons sa valeur en dérivant la fonction de vraisemblance et résolvant cette dérivé égale à 0.
\[ \frac{\delta}{\delta p}L(p|(7;4))=\frac{\delta}{\delta p}.[\frac{7!}{4!(7-4)!}p^4.(1-p)^{7-4}]=0 \]
Il est plus facile de maximiser la log vraisemblance et cela donne le même résultat.
\[ \frac{\delta}{\delta p}ln(L(p|(7;4)))=\frac{\delta}{\delta p}.ln([\frac{7!}{4!(7-4)!}p^4.(1-p)^{7-4}]) \]
\[ \frac{\delta}{\delta p}ln(L(p|(7;4)))=\frac{\delta}{\delta p}.[ln(\frac{7!}{4!(7-4)!})+ln(p^4)+ln((1-p)^{7-4})] \]
\[ \frac{\delta}{\delta p}ln(L(p|(7;4)))=\frac{\delta}{\delta p}.[ln(\frac{7!}{4!(7-4)!})+4.ln(p)+(7-4).ln(1-p)] \]
Dérivons l’expression simplifiée.
\[ \frac{\delta}{\delta p}ln(L(p|(7;4)))=0+4\frac{1}{p}-3\frac{1}{1-p} \]
\[ \frac{\delta}{\delta p}ln(L(p|(7;4)))=\frac{4}{p}-\frac{3}{1-p}=0 \]
Il ne nous reste plus qu’à sortir p.
\[ \frac{4}{p}-\frac{3}{1-p}=0 \]
Multipliions les deux membres par \(\frac{1}{1-p}\).
\[ 4.(1-p)-3.p=0 \]
\[ 4-4p-3p=0 \]
\[ -7p=-4 \]
\[ p=\frac{4}{7}=0,57 \]
La valeur de p permettant de maximiser la vraisemblance est 57%. Cela correspond à la fréquence d’observation d’évènement réussite au regard du nombre d’expérience. Voyons cela sur notre graphe.
ggplot(data=dat,aes(x=p,y=L))+
geom_line(color='red',linewidth=1)+
geom_segment(aes(x=4/7,xend=4/7,
y=0,
yend=dbinom(4,7,prob=4/7)),
linetype='dashed',color='blue')+
labs(y="Vraisemblance")+
coord_cartesian(expand=FALSE,ylim=c(0,0.35))+
theme_minimal()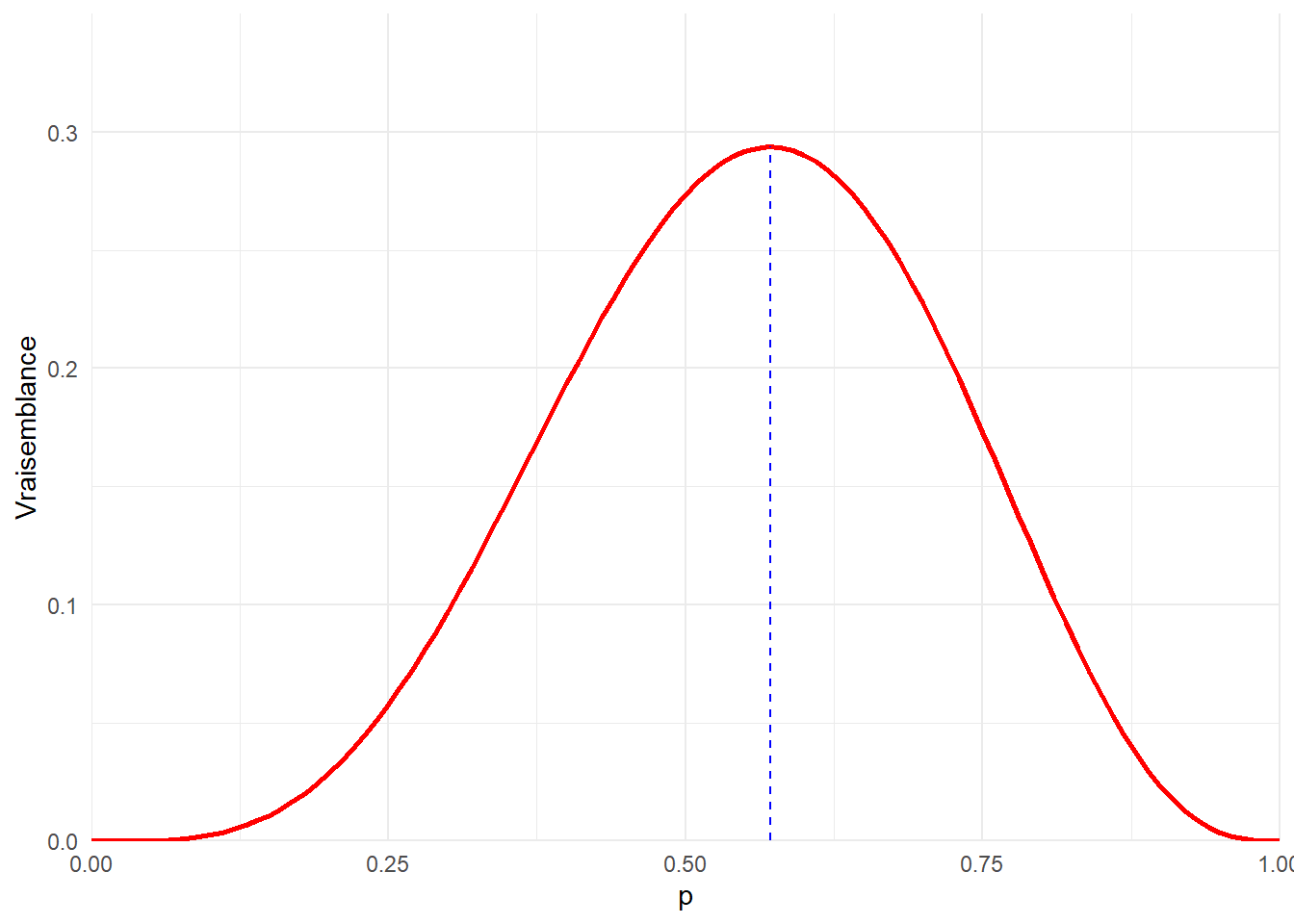
Maximun de vraisemblance pour une distribution normale
Revenons maintenant à notre loi normale début. Elle comprend deux paramètres l’espérance mathématique et l’écart type. Écrivons sa vraisemblance pour n observations independantes de x.
\[ L[N(\mu,\sigma)|x_1,x_2,...,x_n]=L[N(\mu,\sigma)|x_1]\times L[N(\mu,\sigma)|x_2]\times ...\times L[N(\mu,\sigma)|x_n] \]
\[ L[N(\mu,\sigma)|x_1,x_2,...,x_n]= \frac{1}{\sigma\sqrt{2\pi}}e^{-\frac{1}{2}(\frac{x_1-\mu}{\sigma})^2}\times \frac{1}{\sigma\sqrt{2\pi}}e^{-\frac{1}{2}(\frac{x_2-\mu}{\sigma})^2}\times ...\times \frac{1}{\sigma\sqrt{2\pi}}e^{-\frac{1}{2}(\frac{x_n-\mu}{\sigma})^2} \]
Ici, la fonction de répartition de la loi normale est exprimée à partir de l’écart type. Il est plus pratique de travailler à partir de la variance repassons donc à la forme incluant cette dernière.
\[ L[N(\mu,\sigma)|x_1,x_2,...,x_n]= \frac{1}{\sqrt{2\pi\sigma^2}}e^{-\frac{(x_1-\mu)^2}{2.\sigma^2}}\times \frac{1}{\sqrt{2\pi\sigma^2}}e^{-\frac{(x_2-\mu)^2}{2.\sigma^2}}\times ...\times \frac{1}{\sqrt{2\pi\sigma^2}}e^{-\frac{(x_n-\mu)^2}{2.\sigma^2}} \]
Il est également plus facile de travailler à partir de la log vraisemblance qui produit le même maximum que la vraisemblance. Utilisons la et commençons la simplification de l’expression.
\[ ln(L[N(\mu,\sigma)|x_1,x_2,...,x_n])=ln( \frac{1}{\sqrt{2\pi\sigma^2}}e^{-\frac{(x_1-\mu)^2}{2.\sigma^2}}\times ...\times \frac{1}{\sqrt{2\pi\sigma^2}}e^{-\frac{(x_n-\mu)^2}{2.\sigma^2}}) \]
\[ ln(L[N(\mu,\sigma)|x_1,x_2,...,x_n])=ln(\frac{1}{\sqrt{2\pi\sigma^2}}e^{-\frac{(x_1-\mu)^2}{2.\sigma^2}})+...+ ln(\frac{1}{\sqrt{2\pi\sigma^2}}e^{-\frac{(x_n-\mu)^2}{2.\sigma^2}}) \]
On a un terme identique à l’index prés qui s’additionne n fois. Limitons nous au premier pour simplifier l’écriture.
\[ ln(\frac{1}{\sqrt{2\pi\sigma^2}}e^{-\frac{(x_1-\mu)^2}{2.\sigma^2}}) \]
\[ ln(\frac{1}{\sqrt{2\pi\sigma^2}})+ln(e^{-\frac{(x_1-\mu)^2}{2.\sigma^2}}) \]
Passons la racine carrée en puissance.
\[ ln((\sigma^22\pi)^{-1/2})-\frac{(x_1-\mu)^2}{2.\sigma^2} \]
\[ -\frac{1}{2}ln(\sigma^22\pi)-\frac{(x_1-\mu)^2}{2.\sigma^2} \]
\[ -\frac{1}{2}ln(2\pi)-\frac{1}{2}ln(\sigma^2)-\frac{(x_1-\mu)^2}{2.\sigma^2} \]
\[ -\frac{1}{2}ln(2\pi)-ln(\sigma)-\frac{(x_1-\mu)^2}{2.\sigma^2} \]
Utilisons l’expression dans la formule générale.
\[ ln(L[N(\mu,\sigma)|x_1,x_2,...,x_n])=-\frac{1}{2}ln(2\pi)-ln(\sigma)-\frac{(x_1-\mu)^2}{2.\sigma^2}-... -\frac{1}{2}ln(2\pi)-ln(\sigma)-\frac{(x_n-\mu)^2}{2.\sigma^2} \]
On a la même expression qui se répété n fois à l’index de x prés. Simplifions les choses.
\[ ln(L[N(\mu,\sigma)|x_1,x_2,...,x_n])=-\frac{n}{2}ln(2\pi)-n.ln(\sigma)-\frac{(x_1-\mu)^2}{2.\sigma^2}-...-\frac{(x_n-\mu)^2}{2.\sigma^2} \]
Maintenant que nous avons l’expression simplifié de la log vraisemblance de la loi normale, il s’agit de la dérivé en fonction de nos différents paramètre. Commençons par dériver par \(\mu\).
\[ \frac{\delta.ln(L[N(\mu,\sigma)|x_1,x_2,...,x_n])}{\delta \mu}=\frac{\delta}{\delta \mu}[-\frac{n}{2}ln(\sqrt{2\pi})-n.ln(\sigma)-\frac{(x_1-\mu)^2}{2.\sigma^2}-...-\frac{(x_n-\mu)^2}{2.\sigma^2}] \]
\[ \frac{\delta.ln(L[N(\mu,\sigma)|x_1,x_2,...,x_n])}{\delta \mu}=\frac{\delta}{\delta \mu}[-\frac{(x_1-\mu)^2}{2.\sigma^2}-...-\frac{(x_n-\mu)^2}{2.\sigma^2}] \]
On a la dérivé d’un quotient appliquons la régles des dérivation en chaine.
\[ \frac{\delta.ln(L[N(\mu,\sigma)|x_1,x_2,...,x_n])}{\delta \mu}=\frac{x_1-\mu}{\sigma^2}-...-\frac{x_n-\mu}{\sigma^2} \]
Simplifions l’expression en mettant $ $ en facteur.
\[ \frac{\delta.ln(L[N(\mu,\sigma)|x_1,x_2,...,x_n])}{\delta \mu}=\frac{1}{\sigma^2}[(x_1+...+x_n)-n.\mu] \]
On a notre dérivé en fonction de notre premier paramètre. Dérivons en fonction de notre second, \(\sigma\).
\[ \frac{\delta.ln(L[N(\mu,\sigma)|x_1,x_2,...,x_n])}{\delta \sigma}=\frac{\delta}{\delta \sigma}[-\frac{n}{2}ln(\sqrt{2\pi})-n.ln(\sigma)-\frac{(x_1-\mu)^2}{2.\sigma^2}-...-\frac{(x_n-\mu)^2}{2.\sigma^2}] \]
\[ \frac{\delta.ln(L[N(\mu,\sigma)|x_1,x_2,...,x_n])}{\delta \sigma}=-\frac{n}{\sigma}+\frac{(x_1 -\mu)^2}{\sigma^3}+...+\frac{(x_n -\mu)^2}{\sigma^3} \]
Simplifions l’expression en mettons \(\frac{1}{\sigma^3}\) en facteur.
\[ \frac{\delta.ln(L[N(\mu,\sigma)|x_1,x_2,...,x_n])}{\delta \sigma}=-\frac{n}{\sigma}+\frac{1}{\sigma^3}[(x_1 -\mu)^2+...+(x_n -\mu)^2] \]
Maintenant que l’on a nos dérivées, il s’agit de trouver les valeurs des paramètres permettant de les égaliser à 0. Commençons par la dérivée par rapport à \(\mu\).
\[ \frac{1}{\sigma^2}[(x_1+...+x_n)-n.\mu]=0 \]
\[ (x_1+...+x_n)-n.\mu=0 \]
\[ n.\mu=(x_1+...+x_n) \]
\[ \mu=\frac{x_1+...+x_n}{n} \]
On montre ainsi que l’estimateur de \(\mu\) par le maximum de vraisemblance est la moyenne empirique.
Considérons de la même manière la dérivée de notre fonction de log vraisemblance par rapport à sigma.
\[ -\frac{n}{\sigma}+\frac{1}{\sigma^3}[(x_1 -\mu)^2+...+(x_n -\mu)^2]=0 \]
\[ -n+\frac{1}{\sigma^2}[(x_1 -\mu)^2+...+(x_n -\mu)^2]=0 \]
\[ \frac{1}{\sigma^2}[(x_1 -\mu)^2+...+(x_n -\mu)^2]=n \]
\[ (x_1 -\mu)^2+...+(x_n -\mu)^2=n.\sigma^2 \]
\[ \sigma^2=\frac{(x_1-\mu)^2+...+(x_n -\mu)^2}{n} \]
\[ \sigma=\sqrt{\frac{(x_1-\mu)^2+...+(x_n -\mu)^2}{n}} \]
L’estimateur via le maximum de vraisemblance de l’écart type d’une variable aléatoire suivant une loi normale est l’écart type des données.
On a ici un estimateur biaisé puisque :
\[ E(\hat\sigma^2)=\frac{n-1}{n}\sigma^2 \]
Pour rappel, l’estimateur sans biais de la variance est :
\[ \hat\sigma^2=\frac{1}{n+1}\sum^n_{i=1}(x_i-\mu)^2 \]