travailler sur la distance aux extrèmes ?

Commençons par le minimum. Si on observe une tendance au réchauffement, il devrait y avoir de plus en plus d’observations qui s’éloignent du minimum. Établissons donc, comme base de travail, une mesure de la distance au minimum et voyons ce que l’on peut en faire. Prenons simplement la différence entre la température constatée et le minimum.

dat <- dat %>% mutate(min=min(deg_C),
                      dist_min=deg_C-min)
head(dat)

## # A tibble: 6 x 4
##   annee deg_C   min dist_min
##   <dbl> <dbl> <dbl>    <dbl>
## 1  1772  9.17  7.43     1.74
## 2  1773  9.29  7.43     1.86
## 3  1774  9.08  7.43     1.65
## 4  1775 10.1   7.43     2.67
## 5  1776  9.01  7.43     1.58
## 6  1777  9.11  7.43     1.68

Voyons à quoi ressemble la variable au travers d’une série de statistiques descriptives.

dat %>% summarise(Mim.=min(dist_min),
                  prem_quart=quantile(dist_min,probs=.25),
                  mediane=median(dist_min),
                  trois_quart=quantile(dist_min,probs=.75),
                  Max.=max(dist_min),
                  moyenne=mean(dist_min),
                  S.d.=sd(dist_min))

## # A tibble: 1 x 7
##    Mim. prem_quart mediane trois_quart  Max. moyenne  S.d.
##   <dbl>      <dbl>   <dbl>       <dbl> <dbl>   <dbl> <dbl>
## 1     0       1.58     1.9        2.39  3.52    1.96 0.661

Produisons le nuage de points des distances au minimum sur les années d’observations. Pour marquer la valeur de référence (distance 0), traçons une ligne pointillée horizontale pour y=0 et une ligne verticale pleine bleu pour marquer l’année la plus froide (1879).

ggplot(dat)+
  aes(annee,dist_min)+
  geom_point()+
  geom_hline(yintercept=0,linetype='dashed')+
  geom_vline(xintercept = dat$annee[dat$dist_min==0], color='blue')+
  labs(y='écarts par rapport au minimum')+
  coord_cartesian(xlim=c(1770,2022),
                  ylim=c(-0.1,3.6),
                  expand=FALSE)+
  scale_x_continuous(breaks = seq(1770,2025,20))+
  scale_y_continuous(breaks = seq(0,3.5,0.5))+
  theme_bw()+
  theme(axis.title.x=element_blank())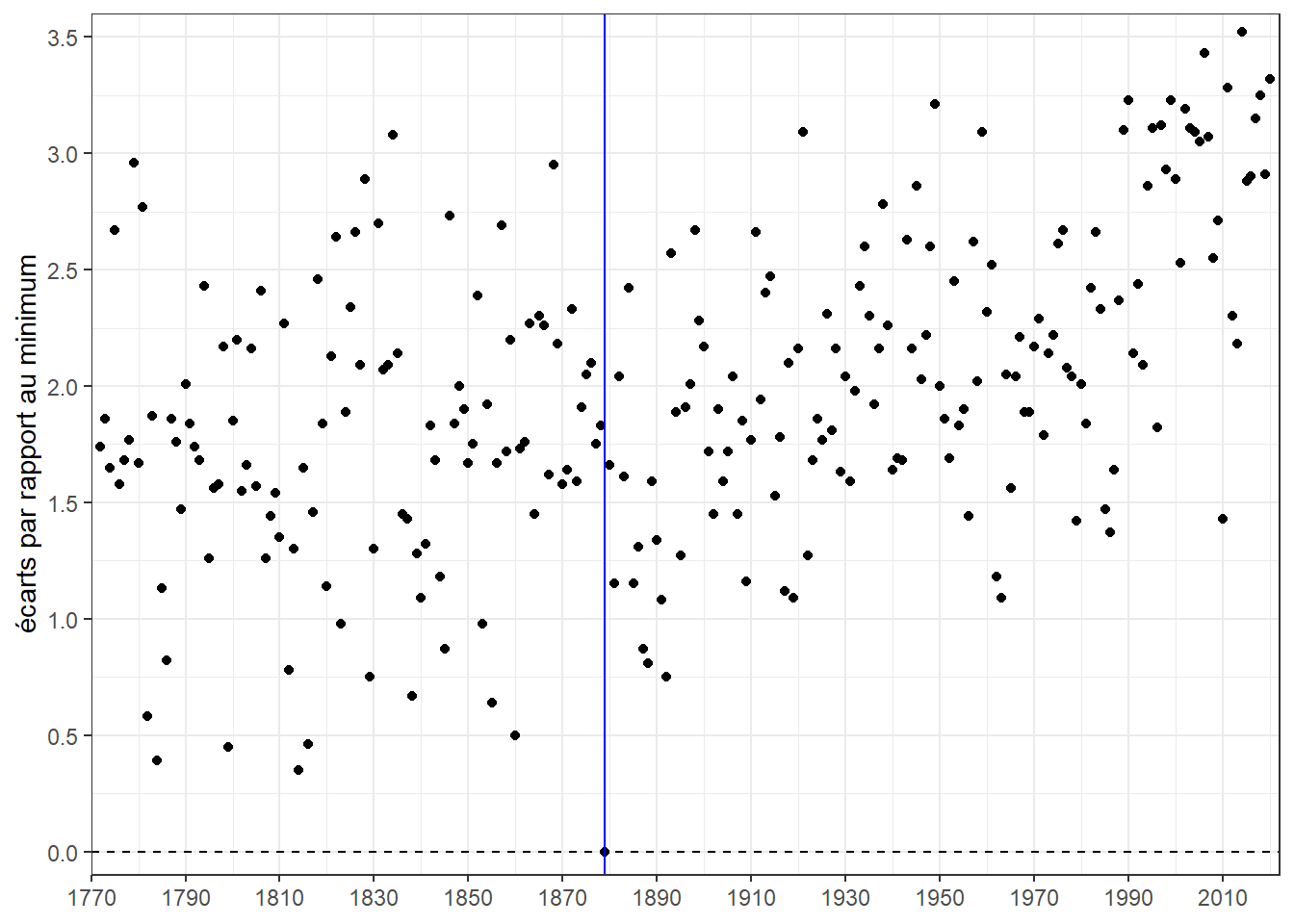

Sans surprise, le nuage a exactement la même forme que celui des températures. Il n’est donc pas plus informatif que celui que nous avons fait dans les posts précédents (celui avec la courbe de tendance). Pour l’améliorer, faisons varier la couleur des points en fonction de la distance au minimum. Une concentration de point de la couleur marquant la distance la plus élevée en fin de période d’observation (les années les plus récentes) indiquera la tendance au réchauffement.

L’opération consiste à ajouter une variable esthétique pour la couleur dans (aes()).

ggplot(dat)+
  aes(annee,dist_min,color=dist_min)+
  geom_point()+
  geom_hline(yintercept=0,linetype='dashed')+
  geom_vline(xintercept = dat$annee[dat$dist_min==0], color='blue')+
  labs(y='écarts par rapport au minimum')+
  coord_cartesian(xlim=c(1770,2022),
                  ylim=c(-0.1,3.6),
                  expand=FALSE)+
  scale_x_continuous(breaks = seq(1770,2025,20))+
  scale_y_continuous(breaks = seq(0,3.5,0.5))+
  theme_bw()+
  theme(axis.title.x=element_blank())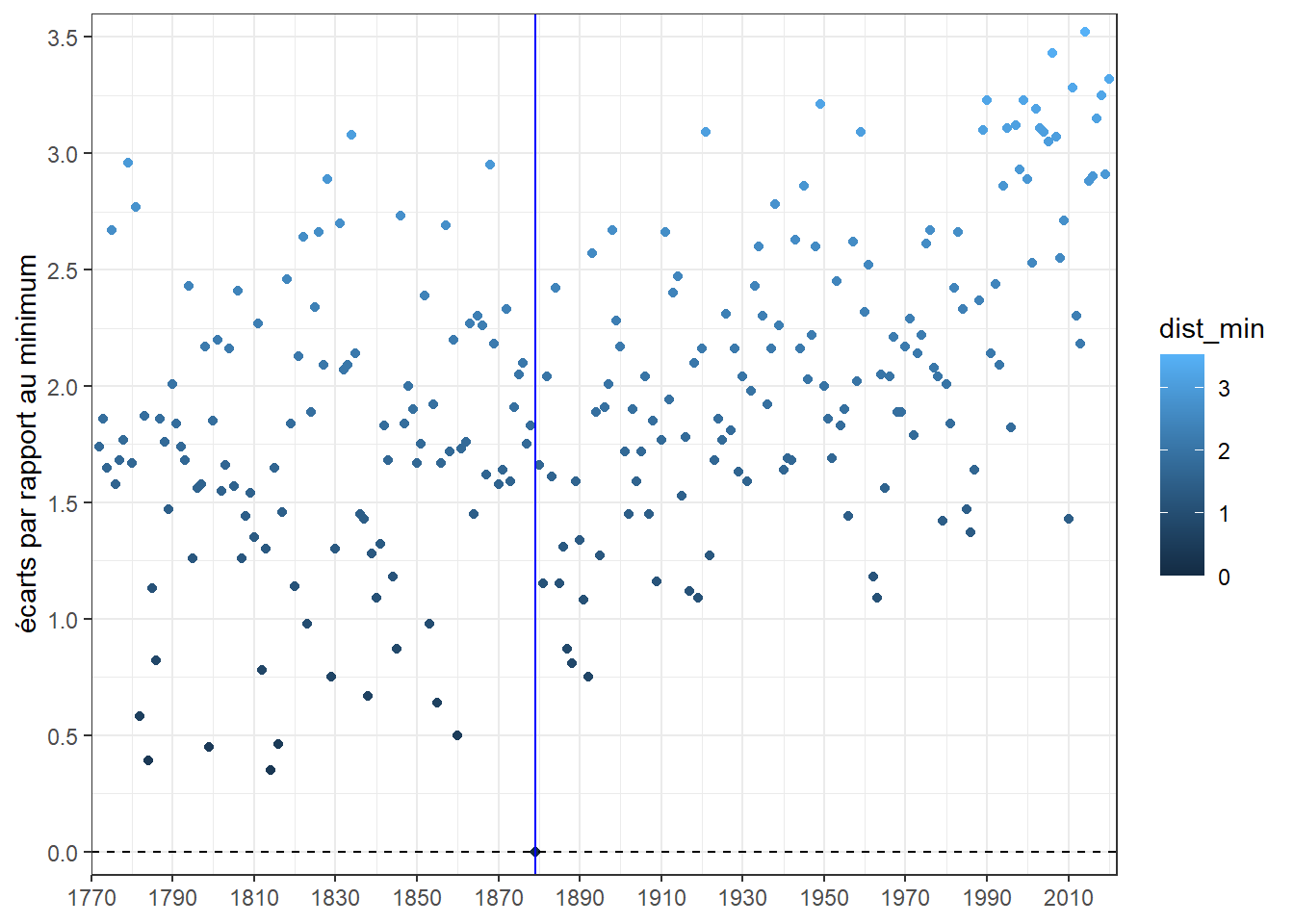

On voit bien une concentration de points plus clairs sur les dernières années marquant ainsi le réchauffement. Néanmoins, on pourrait reprocher au graphe le choix de la couleur bleu souvent assimilé à une gradation vers le froid (plus clair, plus froid). Hors, ici c’est loin d’être le cas. Choisissons une autre forme de dégradé plus parlante. Pour cela, chargeons le package viridis qui en propose de nombreux à associer ainsi que son propre complément d’échelle pour GGPLOT2 : le scale_fill_viridis(). Pour un aperçu des progressions proposées, vous pouvez consulter le site associé au package. Un des avantages de ces dernières est d’être conçu pour que même une personne daltonienne puisse distinguer les nuances. Choisissons la progression appelée plasma qui va du violet sombre au jaune clair.

library(viridis)
ggplot(dat)+
  geom_point(aes(x=annee,y=dist_min,fill=dist_min),shape=21,colour='black',size=2)+
  geom_hline(yintercept=0,linetype='dashed')+
  geom_vline(xintercept = dat$annee[dat$dist_min==0], color='blue')+
  coord_cartesian(xlim=c(1770,2022),
                  ylim=c(-0.1,3.6),
                  expand=FALSE)+
  scale_x_continuous(breaks = seq(1770,2025,20))+
  scale_y_continuous(breaks = seq(0,3.5,0.5))+
  labs(y='écarts par rapport au minimum')+
  scale_fill_viridis(option="plasma")+
  guides(fill=guide_colorbar(title="éloignement au minimum",
                             title.position = 'top',title.hjust=0.5,
                             barwidth=unit(20,'lines'),
                             barheight = unit(0.5,'lines')))+
  theme_bw()+
  theme(legend.position = 'top',
        axis.title.x = element_blank())

C’est mieux, mais toujours pas très différent de notre graphe d’origine. Faisons la même chose avec la température maximale. Calculons la distance associée en veillant à passer l’ensemble à la valeur absolue pour garantir que les distances soient toujours positives.

dat <- dat %>% mutate(max=max(deg_C),
                      dist_max=abs(deg_C-max))
head(dat)

## # A tibble: 6 x 6
##   annee deg_C   min dist_min   max dist_max
##   <dbl> <dbl> <dbl>    <dbl> <dbl>    <dbl>
## 1  1772  9.17  7.43     1.74  11.0     1.78
## 2  1773  9.29  7.43     1.86  11.0     1.66
## 3  1774  9.08  7.43     1.65  11.0     1.87
## 4  1775 10.1   7.43     2.67  11.0     0.85
## 5  1776  9.01  7.43     1.58  11.0     1.94
## 6  1777  9.11  7.43     1.68  11.0     1.84

Pour réaliser le graphe, choisissons une progression de couleurs différentes. Disons celle nommée rocket.

ggplot(dat)+
  geom_point(aes(x=annee,y=dist_max,fill=dist_max),shape=21,colour='black',size=2)+
  geom_hline(yintercept=0,linetype='dashed')+
  geom_vline(xintercept = dat$annee[dat$dist_max==0], color='red')+
  coord_cartesian(xlim=c(1770,2022),
                  ylim=c(-0.1,3.6),
                  expand=FALSE)+
  scale_x_continuous(breaks = seq(1770,2025,20))+
  scale_y_continuous(breaks = seq(0,3.5,0.5))+
  labs(y='écarts par rapport au maximum')+
  scale_fill_viridis(option="rocket")+
  guides(fill=guide_colorbar(title="éloignement au maximum",
                             title.position = 'top',title.hjust=0.5,
                             barwidth=unit(20,'lines'),
                             barheight = unit(0.5,'lines')))+
  theme_bw()+
  theme(legend.position = 'top',
        axis.title.x = element_blank())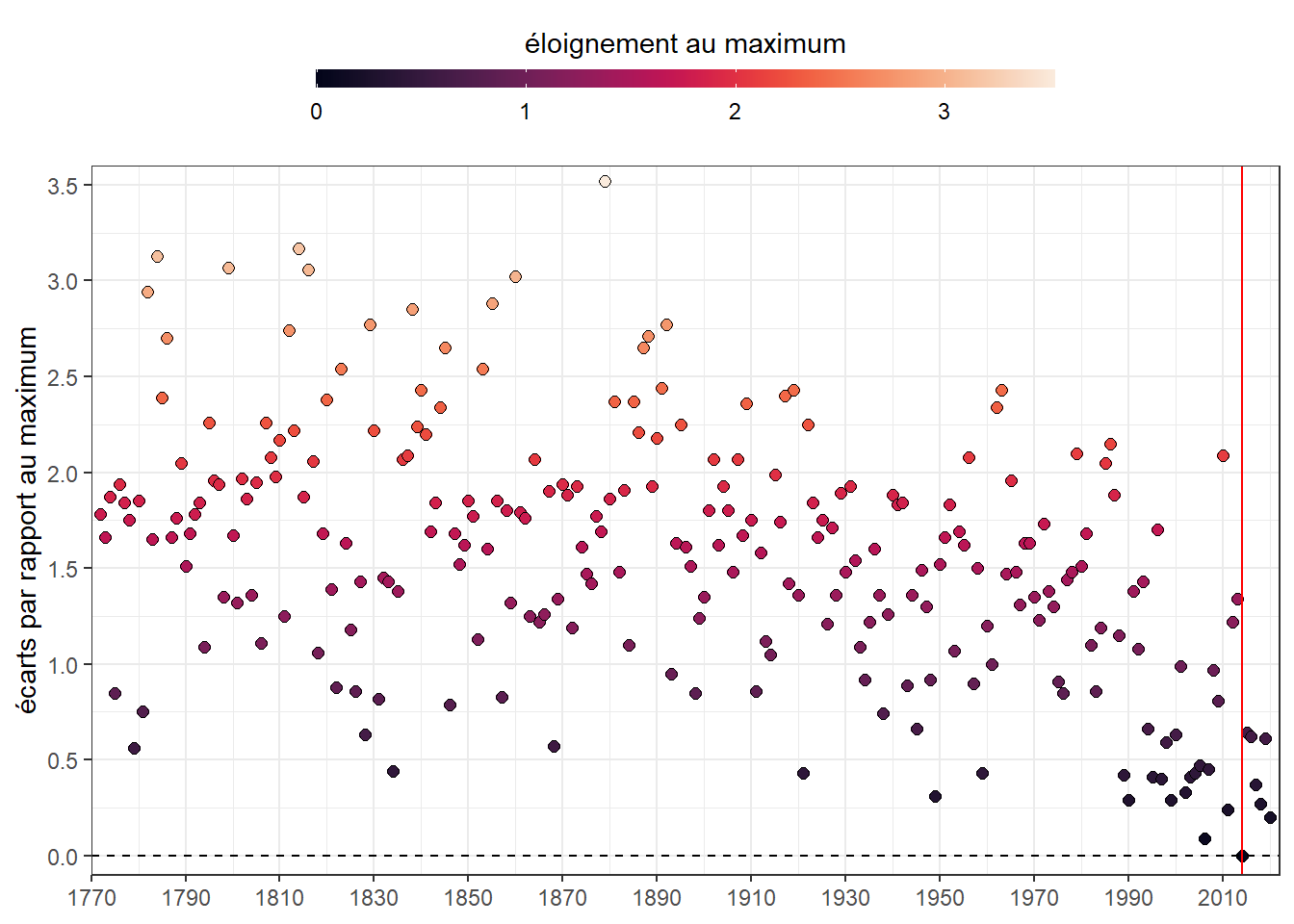

On peut noter que la forme du nuage est renversé par rapport au graphe d’origine (et à celui de la distance au minimum), ce qui était attendu. Pour le reste, il a la même forme. On voit bien une concentration de points plus sombres, ici les années les plus proches, en bas à droite (proche du maximum) manquant ainsi le réchauffement.

Encore une fois, on rien de très innovant dans la présentation. Essayons un nuage de points présentant les distances aux extrêmes en coordonné et l’année de mesure comme couleur pour les points. Compte tenu du nombre de ces derniers et pour bien marquer les différences, prenons une progressions intégrant deux couleurs. Choisissons celle nommée turbo.

ggplot(dat,aes(dist_min,dist_max,color=annee))+
  geom_point()+
  labs(x='distances au minimum',y='distances au maximum')+
  coord_cartesian(xlim=c(-0.1,3.6),ylim=c(-0.1,3.6),expand=FALSE)+
  scale_x_continuous(breaks=seq(0,3.5,0.25))+
  scale_y_continuous(breaks=seq(0,3.5,0.25))+
  scale_color_viridis(option="turbo")+
  guides(color=guide_colorbar(title="année",
                              title.position = 'top',
                              title.hjust=0.5,
                              barwidth=unit(20,'lines'),
                              barheight = unit(0.5,'lines')))+
  theme_bw()+
  theme(legend.position = 'top')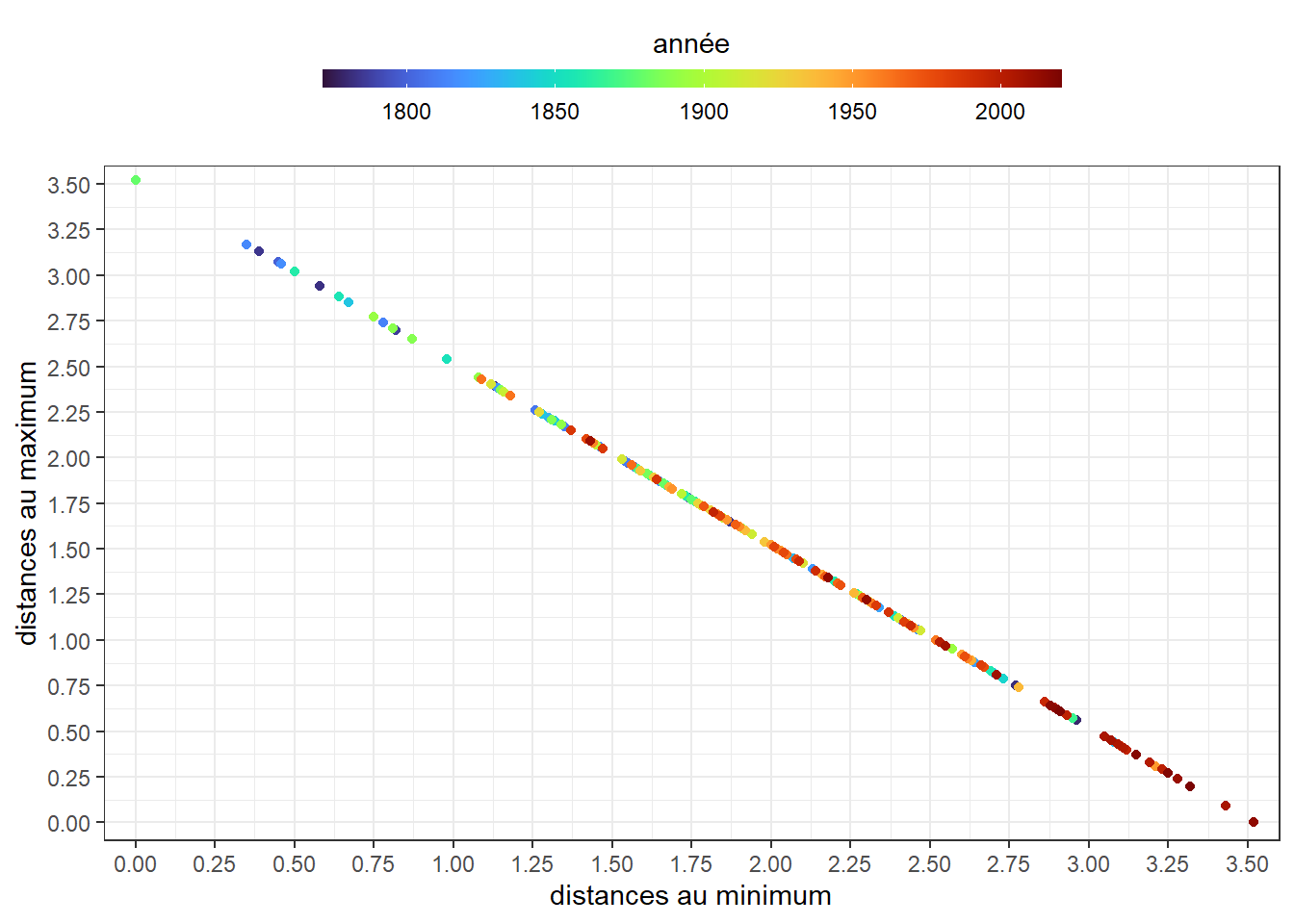

Les points s’articulent sur une droite à 45° tombante avec les années les plus proches du maximum sont plus fréquemment marquées par des points plus rouges, elles sont donc plus récentes, et les plus proches du minimum par des points plus bleus, elles sont donc plus anciennes. On note que les couleurs associées aux années les plus récentes sont majoritairement située sur le bas et ce qui une nouvelle fois la marque du réchauffement.

Vous me direz on pourrait faire la même chose en utilisant un seul axe. Faisons-le sur la distance au minimum.

ggplot(dat)+
  geom_hline(yintercept = 0,linetype='dashed')+
  geom_point(aes(x=dist_min,y=0,color=annee))+
  labs(x='distances au minimum')+
  coord_cartesian(xlim=c(-0.1,3.6),ylim=c(-0.01,0.01),expand=FALSE)+
  scale_x_continuous(breaks=seq(0,3.5,0.25))+
  scale_color_viridis(option="turbo")+
  guides(color=guide_colorbar(title="année",
                              title.position = 'top',
                              title.hjust=0.5,
                              barwidth=unit(20,'lines'),
                              barheight = unit(0.5,'lines')))+
  theme_bw()+
  theme(legend.position = 'top',
        panel.grid = element_blank(),
        axis.text.y  = element_blank(),
        axis.title.y = element_blank())

On retrouve la concentration points rouges marquant les dernières années sur la droite de l’axe (au-dessus de la distance de 3). Néanmoins, on peut se demander si cela n’est pas un effet d’optique dû à la superposition des points sur l’axe. Les points foncés cachent les points clairs en cas de superposition. Pour éviter cette difficulté, on peut répartir les points aléatoirement au-dessus et en-dessous de l’axe pour limiter le chevauchement. Pour cela, dans l’option position du geom_point(), j’utilise la fonction position_jitter() qui va les répartir aléatoirement en précisant que la bande de fluctuation verticale est comprise entre -0.005 et +0.005 (l’option seed assure la reproductibilité du tirage aléatoire).

ggplot(dat)+
  geom_hline(yintercept = 0,linetype='dashed')+
  geom_point(aes(x=dist_min,y=0,fill=annee),
             shape=21,
             position = position_jitter(height = 0.005,
                                        seed=5))+
  labs(x='distances au minimum')+
  coord_cartesian(xlim=c(-0.1,3.6),ylim=c(-0.01,0.01),expand=FALSE)+
  scale_x_continuous(breaks=seq(0,3.5,0.25))+
  scale_fill_viridis(option="turbo")+
  guides(fill=guide_colorbar(title="année",
                              title.position = 'top',
                              title.hjust=0.5,
                              barwidth=unit(20,'lines'),
                              barheight = unit(0.5,'lines')))+
  theme_bw()+
  theme(legend.position = 'top',
        panel.grid = element_blank(),
        axis.text.y  = element_blank(),
        axis.title.y = element_blank())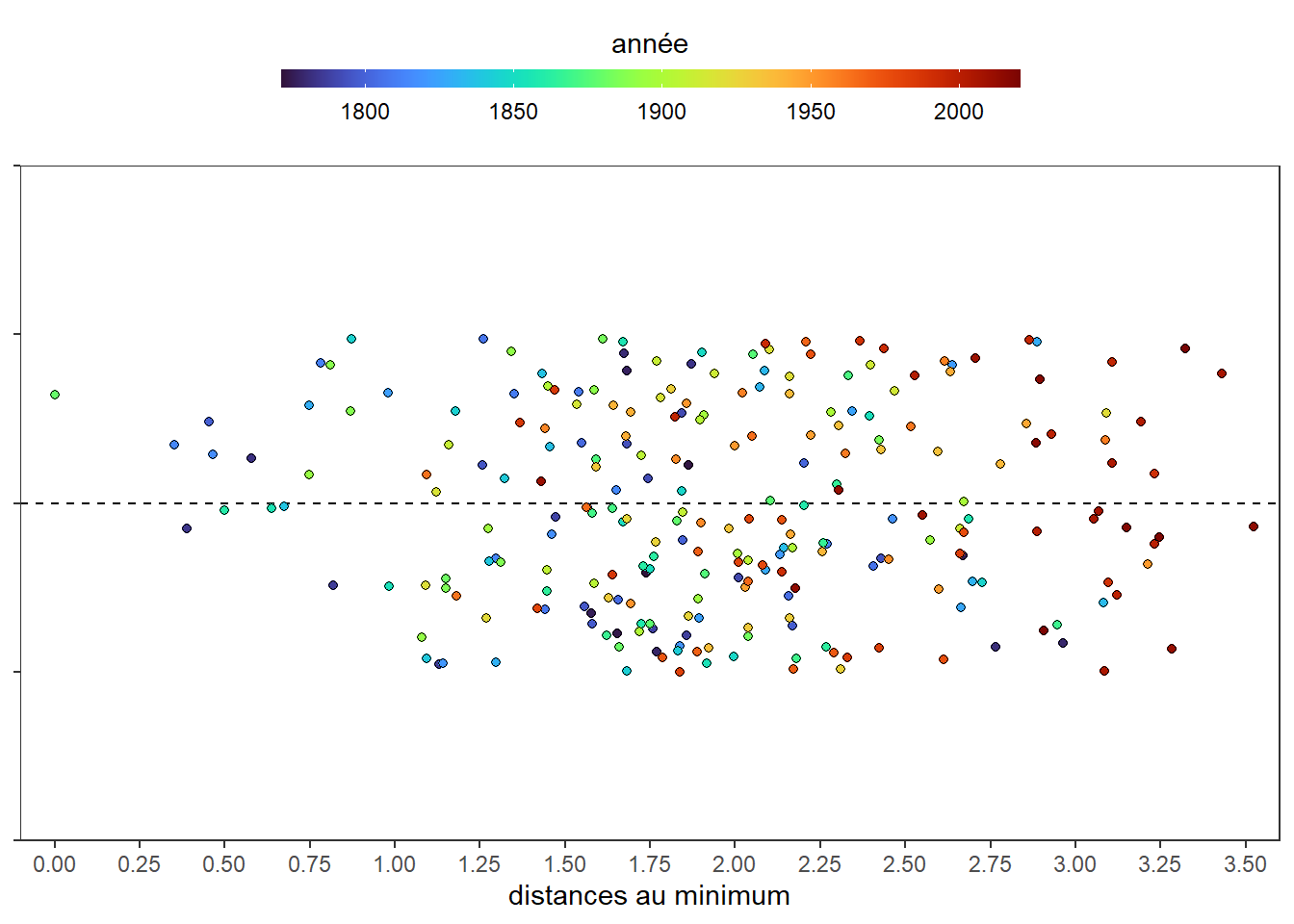

C’est mieux! Il n’y a plus de problèmes de superpositions. Ajoutons un repaire pour isoler les années les température les plus élevés (les observations avec les distances au minimum les plus élevées). Traçons une ligne pointillée verticale à 2.75.

ggplot(dat)+
  geom_hline(yintercept = 0,linetype='dashed')+
  geom_point(aes(x=dist_min,y=0,fill=annee),
             shape=21,
             position = position_jitter(height = 0.005,
                                        seed=5))+
  geom_vline(xintercept = 2.75,linetype='dotted')+
  labs(x='distances au minimum')+
  coord_cartesian(xlim=c(-0.1,3.6),ylim=c(-0.01,0.01),expand=FALSE)+
  scale_x_continuous(breaks=seq(0,3.5,0.25))+
  scale_fill_viridis(option="turbo")+
  guides(fill=guide_colorbar(title="année",
                              title.position = 'top',
                              title.hjust=0.5,
                              barwidth=unit(20,'lines'),
                              barheight = unit(0.5,'lines')))+
  theme_bw()+
  theme(legend.position = 'top',
        panel.grid = element_blank(),
        axis.text.y  = element_blank(),
        axis.title.y = element_blank())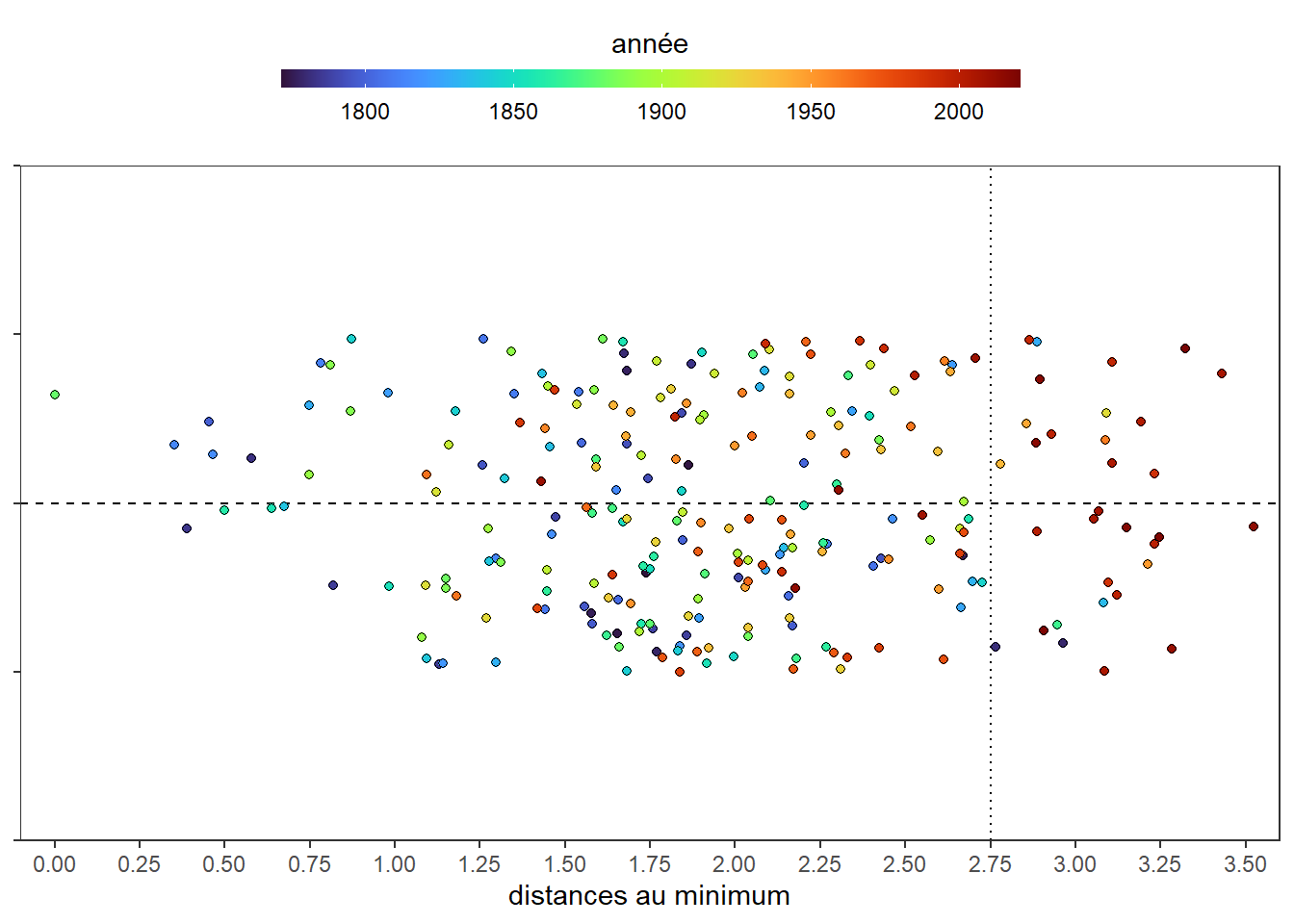

C’est plus clair. Mais, est-ce vraiment nécessaire de travailler avec des distances au minimum. Encore une fois, il apparaît que non. Réalisons le même graphe directement avec les températures en choisissant cette fois le 75ème percentile comme marqueur (9.82) des cas les années les plus chaudes.

ggplot(dat)+
  geom_hline(yintercept = 0,linetype='dashed')+
  geom_point(aes(x=deg_C,y=0,fill=annee),
             shape=21,
             position = position_jitter(height = 0.005,
                                        seed=5))+
  geom_vline(xintercept = 9.820,linetype='dotted')+
  labs(x='°C')+
  coord_cartesian(xlim=c(7.3,11),ylim=c(-0.01,0.01),expand=FALSE)+
  scale_x_continuous(breaks=seq(7.25,11,0.25))+
  scale_fill_viridis(option="turbo")+
  guides(fill=guide_colorbar(title="année",
                              title.position = 'top',
                              title.hjust=0.5,
                              barwidth=unit(20,'lines'),
                              barheight = unit(0.5,'lines')))+
  theme_bw()+
  theme(legend.position = 'top',
        panel.grid = element_blank(),
        axis.text.y  = element_blank(),
        axis.title.y = element_blank())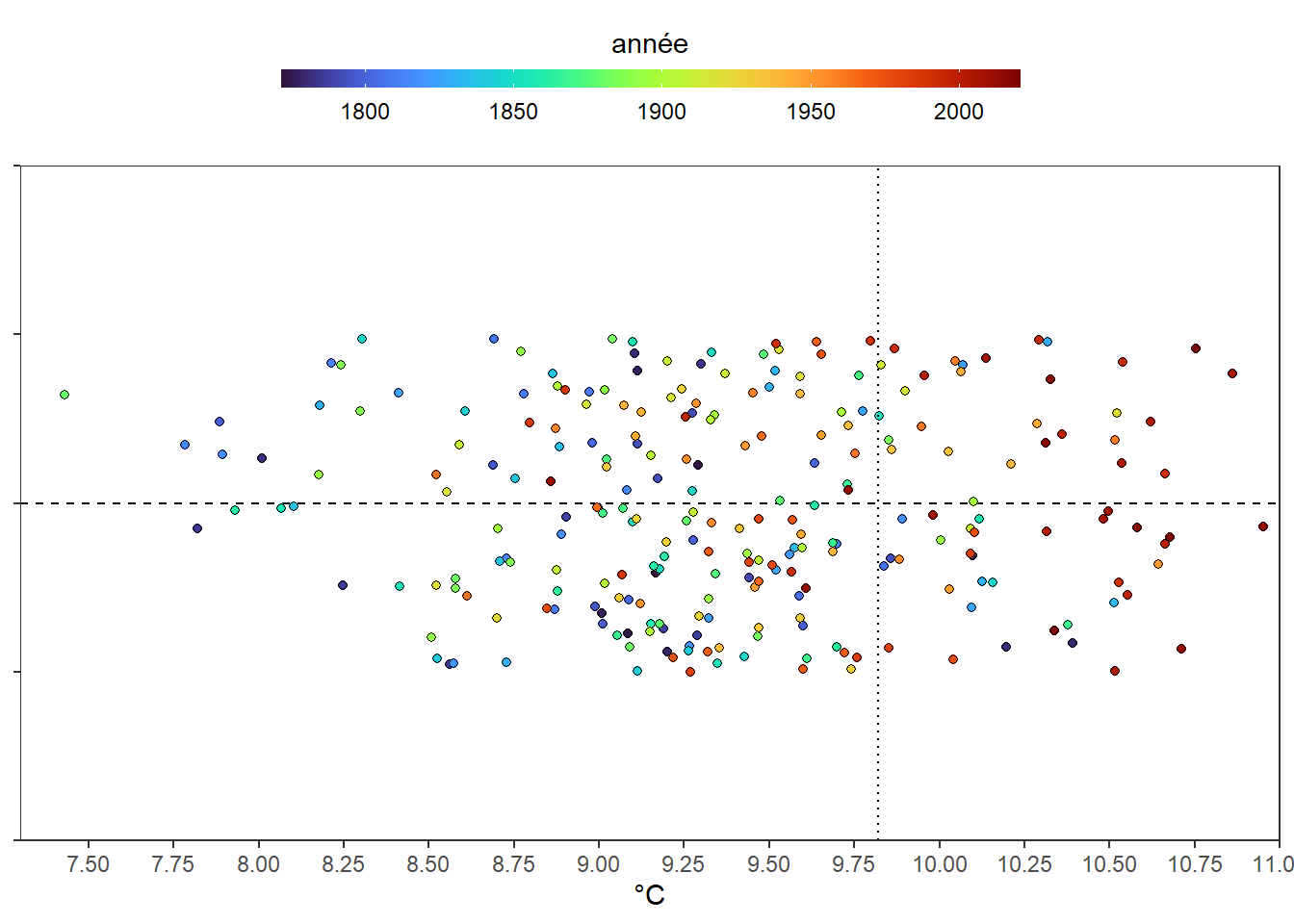

Le graphe est quasi identique au précédent. Bref la distance aux extrêmes, utilisez de la sorte ne donne pas grand chose de plus que les données brutes.

Essayons d’envisager une transformation de cette information, un classement des observations en fonction de leurs distances aux extrêmes. Pour cela, attribuons leur un rang. Le rang 1 marque la position de l’extrême considéré, le rang deux celui des la température venant juste après…

dat$rk_min <- rank(dat$dist_min)
dat$rk_max <- rank(dat$dist_max)
head(dat)

## # A tibble: 6 x 8
##   annee deg_C   min dist_min   max dist_max rk_min rk_max
##   <dbl> <dbl> <dbl>    <dbl> <dbl>    <dbl>  <dbl>  <dbl>
## 1  1772  9.17  7.43     1.74  11.0     1.78   92.5   158.
## 2  1773  9.29  7.43     1.86  11.0     1.66  116.    134.
## 3  1774  9.08  7.43     1.65  11.0     1.87   74.5   176.
## 4  1775 10.1   7.43     2.67  11.0     0.85  212      38 
## 5  1776  9.01  7.43     1.58  11.0     1.94   62     188 
## 6  1777  9.11  7.43     1.68  11.0     1.84   83     167

Notez que certaines observations ont des rangs qui ne sont pas des nombres entiers. C’est tout simplement que sur ces rangs, nous avons des observations présentant la même valeur de la variable de classement (des ex aequo).

Représentons ces rangs au travers de deux courbes, un rouge pour le classement des années les plus chaudes et un bleu pour le classement des années les plus froides. L’abscisse sera le rang et l’ordonnée la distance à l’extrême. Les deux courbes seront bien sûr symétriques par rapport à point un point situé entre elles et se rejoindrons à leurs extrémités. L’année la plus froide a le rang 1 pour la distance au plus froid et le rang 249 pour la distance au plus chaud. L’année la plus chaude a le rang 1 pour la distance au plus chaud et le rang 249 pour la distance au plus froid.

ggplot(dat)+
  geom_line(aes(x=rk_max,
                  y=dist_max),color='red')+
  geom_line(aes(x=rk_min,
                  y=dist_min),color='blue')+
  labs(x="rang",y="ditances")+
  coord_cartesian(xlim=c(-1,251),expand=FALSE)+
  scale_x_continuous(breaks=seq(0,250,25))+
  scale_y_continuous(breaks=seq(0,3.5,.5))+
  theme_bw()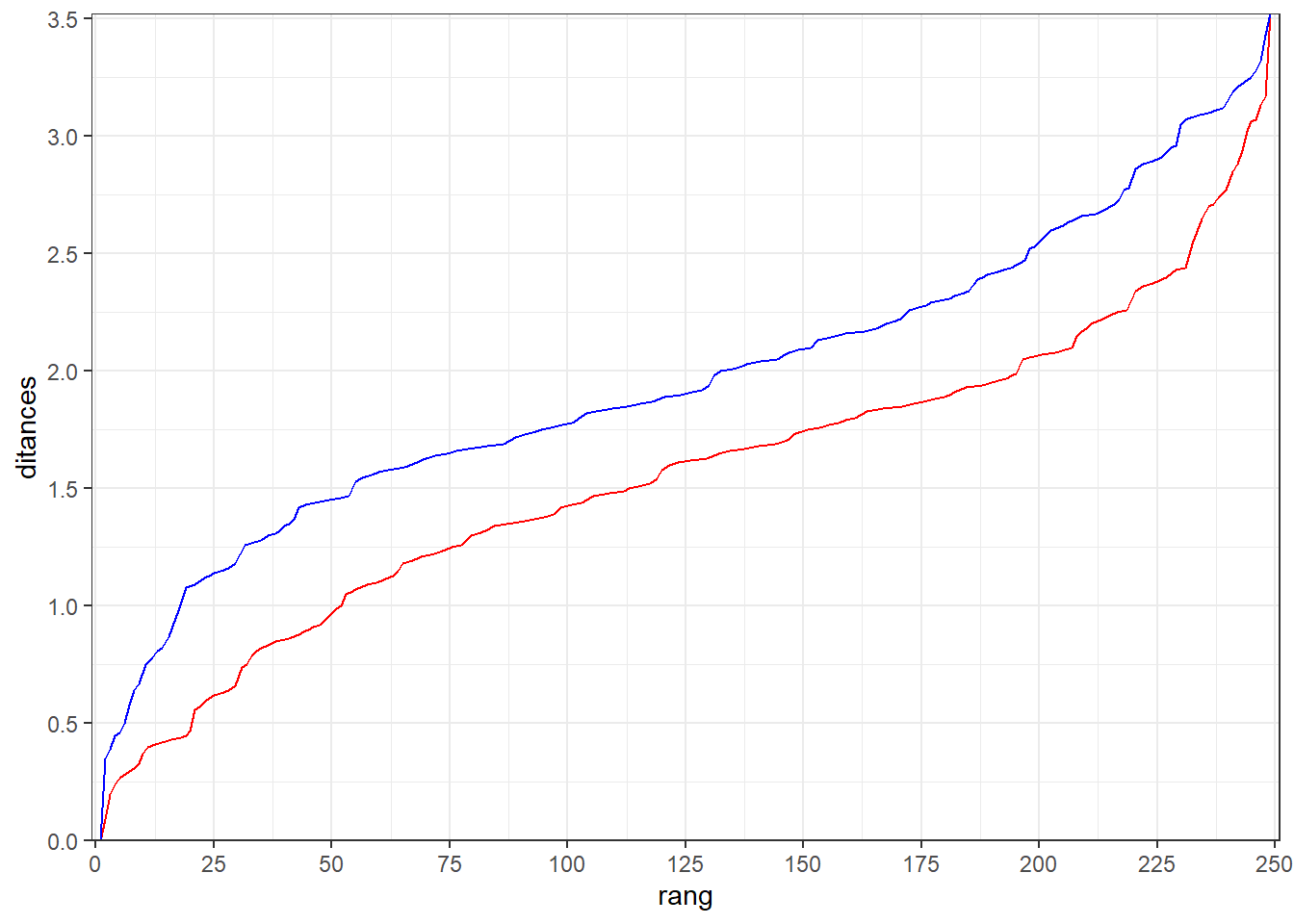

La courbe classant les années des plus froides aux plus chaudes (la bleu) est au-dessus de la courbe classant les années des plus chaudes aux plus froides. Cela indique que la distance à la température la plus froide des années considérées est plus importante que la distance à la température la plus chaude. Autrement-dit, cela indique que l’année la plus froide est plus atypique que l’année la plus chaude.

Pour illustrer ceci, prenons les cas des année de rang 50 en terme de distance à l’année la plus froide et de rang 50 en terme de distance à l’année la plus chaude. La première est 1.5° plus chaude que l’année la plus froide tandis que la seconde n’est que 1° plus froide que l’année la plus chaude. On retrouve ce type de hiérarchie sur l’ensemble des rangs des deux courbes à l’exception évidemment des extrémités.

Ce représentation est intéressante néanmoins elle ne montre pas que les années les plus chaudes sont les plus récentes. Pour en rendre compte, ajoutant des points manquant les 60 dernières années. Si elles sont concentrées sur le haut de la courbe bleu et sur le bas de la courbe rouge, cela marque le réchauffement.

dat<-dat %>% mutate(r_max_50_20=ifelse(annee%in%1960:2020,rk_max,0),
                    r_min_50_20=ifelse(annee%in%1960:2020,rk_min,0))
ggplot(dat)+
  geom_point(aes(r_max_50_20,dist_max))+
  geom_point(aes(x=r_min_50_20,y=dist_min))+
  geom_line(aes(x=rk_max,
                  y=dist_max),color='red')+
  geom_line(aes(x=rk_min,
                  y=dist_min),color='blue')+

  labs(x="rang",y="ditances")+
  coord_cartesian(xlim=c(0,251),expand=FALSE)+
  scale_x_continuous(breaks=seq(0,250,25))+
  scale_y_continuous(breaks=seq(0,3.5,.5))+
  theme_bw()

travailler à partir de dénombrements ?

Une autre stratégie pourrait consister à identifier les années les plus chaudes et à les positionner dans le temps. Pour cela, restructurons notre base. Commençons par identifier les années les plus chaudes. Disons celles pour qui la température moyenne est plus grande que celle représentant le troisième quartile de la distributions (9.82°C). Puis, marquons les décennies afin de dénombrer le nombre des années identifiées comme les plus chaudes intervenant après la décennie considérée. Le résultat est ramené en pourcentage. Par exemple, durant la décennie 1770-1780, on a deux années parmi les plus chaudes (1775 et 1779). Sur un total de 62, il en reste donc 60 au terme cette décennie soit 60/62 autrement-dit 96.8%.

Ajoutons à cela une référence. Pour chaque décennie, établissons la proportion d’années de la période d’analyse restant à courir. Ainsi, par exemple, pour la première décennie 1770-1780, il reste 100% d’années à courir. Pour la seconde décennie 1780-1790, il reste 239/249 soit 96% d’année à courir…

an_chaud<-unlist(dat %>% filter(deg_C>quantile(deg_C,probs=0.75)) %>% select(annee))
decennie<-seq(1770,2020,10)
pr_an_c<-c()
for(i in decennie){
  x<-length(an_chaud[an_chaud>i])/length(an_chaud)
  pr_an_c<-c(pr_an_c,x)
}
rm(x)
prop_an<-c()
for (i in decennie){
  x<-sum(dat$annee>i)/249
  prop_an<-c(prop_an,x)
}  
rm(x)
dat_<-tibble(decennie,pr_an_c,prop_an)
rm(decennie,pr_an_c,prop_an)
head(dat_)

## # A tibble: 6 x 3
##   decennie pr_an_c prop_an
##      <dbl>   <dbl>   <dbl>
## 1     1770   1       1    
## 2     1780   0.968   0.964
## 3     1790   0.952   0.924
## 4     1800   0.935   0.884
## 5     1810   0.919   0.843
## 6     1820   0.903   0.803

Représentons ces éléments nouveaux sur un graphe. Choisissons une courbe pour les années restants à courir et des points rouges pour la proportion des années les plus chaudes survenant après ces différentes décennies.

Optons pour un graphe épuré. Supprimons la titre des axes et faisons en sorte que les gradations soit parlante en elles-mêmes. Pour l’axe des abscisses, indiquons le première année de chaque décennie. Pour l’axe des ordonnées ajoutons à chaque incrément %. Pour cela, utilisons le package scales et indiquons dans l’option label de notre échelle y que l’on utilise la fonction percent.

ggplot(dat_)+aes(x=decennie)+
  geom_point(aes(y=pr_an_c),color='red')+
  geom_line(aes(y=prop_an))+
  scale_y_continuous(breaks=seq(0,1,.1),labels=scales::percent)+
  scale_x_continuous(breaks = seq(1770,2025,20))+
  theme_bw()+
  theme(axis.title= element_blank())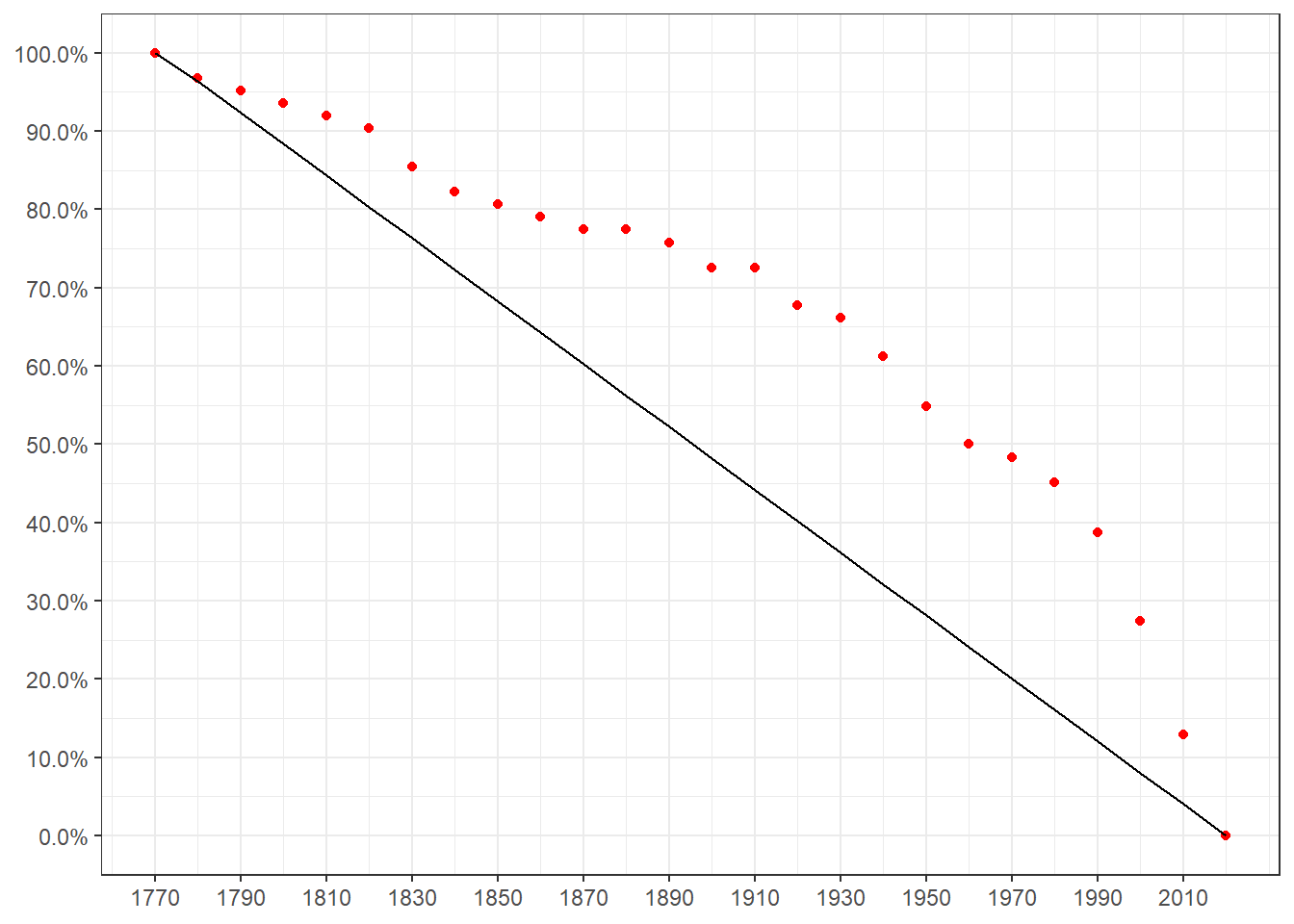

Si les années chaudes se répartissaient uniformément sur la période d’étude (il n’y aurait alors pas de réchauffement), l’ensemble des points se situeraient sur la droite noire. Un point au-dessus d’elle correspond à un renvoi des années les plus chaudes aux décennies les plus récentes (un réchauffement). Un point en-dessus correspond à une période passé particulièrement chaude (un refroidissement).

Ici, on voit bien que les points sont tous au-dessus de la droite (à l’exception des extrémités qui sont mécaniquement sur elle-à la fin de la décennie 2020 tout les années de la période d’observations sont passé chaudes ou non…). On est bien face à un réchauffement. Les points s’éloignent de la droit jusqu’au années 30 puis s’en rapprochent, marquant ainsi la présence plus fréquente des années parmi les plus chaudes. Le rapprochement est plus marqué à compter des années 1980.

On peut par exemple lire sur le graphe qu’on a 54.84% des années les plus chaudes qui se trouvent après 1950 bien que ces années ne représentent que 28.11% de notre échantillon, 50% après 1960, 48.39% après 1970… Si on prend la décennie 2010, elle comprend 12% des années les plus chaudes alors qu’elle ne représente que 4% de l’échantillon. Autrement-dit, sur les 10 années de la décennie, 7 sont parmi les plus chaudes observées depuis 1772.

La représentation utilisée, bien que élégante, présente le défaut d’être difficile à lire qu’en on rentre dans le détail. La différence de distance à la droite oblique entre deux points est difficile à identifier lorsqu’elle est relativement faible.

Pour améliorer les choses, on peut envisager de ne représenter que la différence à la norme (l’equi-répartition des années chaudes sur la période). Faisons-le sur la base d’un nuage de points.

ggplot(dat_)+aes(x=decennie,y=pr_an_c-prop_an)+
  geom_point()+
  scale_y_continuous(breaks=seq(0,0.3,.05),labels=scales::percent)+
  scale_x_continuous(breaks = seq(1770,2025,20))+
  theme_bw()+
  theme(axis.title= element_blank())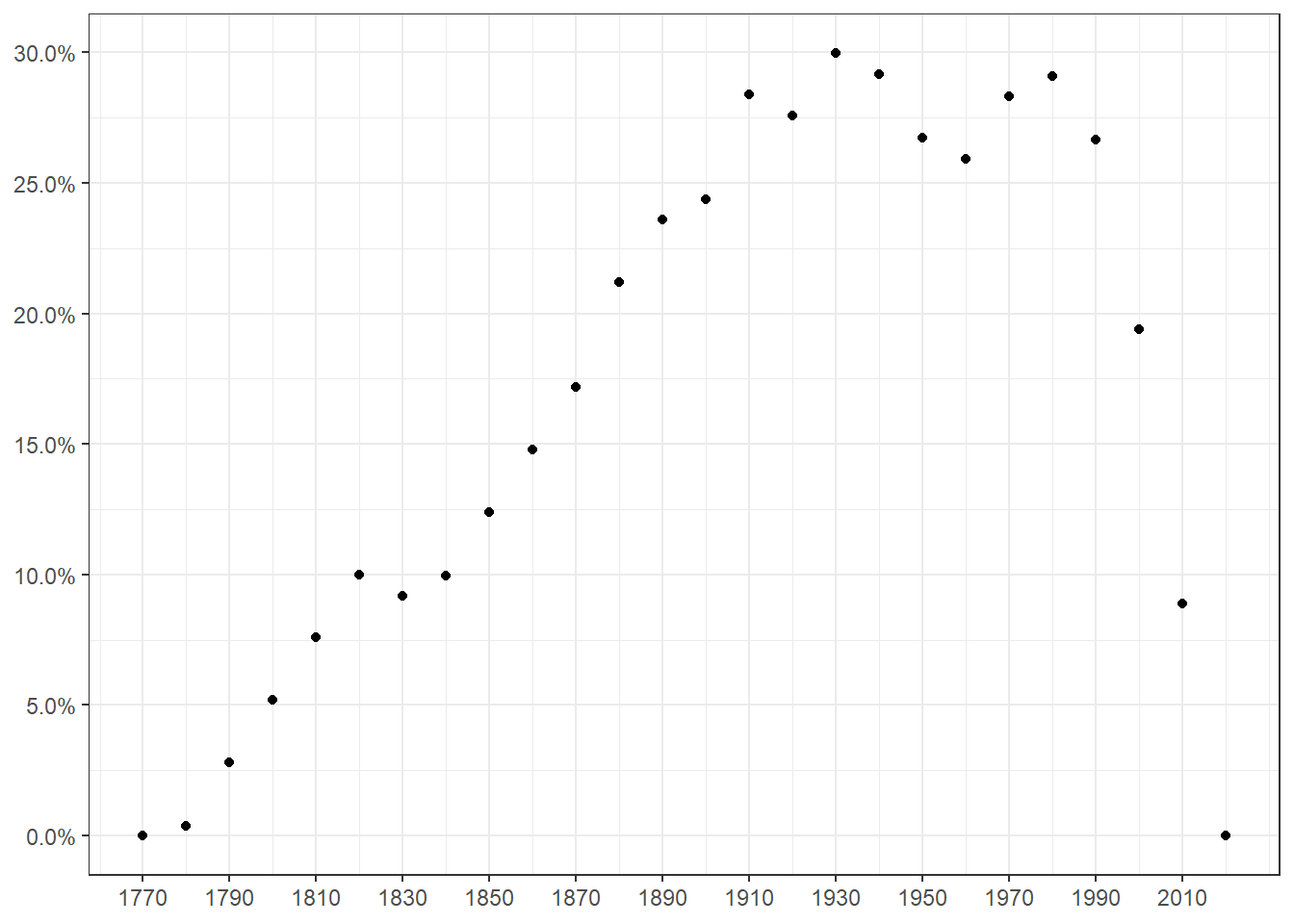

Voyons comment lire le résultat. Prenons, par exemple, la décennie 1810. La proportion d’années chaudes intervenant après 1810 est de 7.5 points de pourcentage supérieur à ce que donnerait une répartition homogène de ces années sur la période d’étude. Pour 1930, cela monte à 30 points ce qui apparaît être le maximum. A partir de là, sachant qu’après 1930, il reste 90 années d’observations, soit 36% du total, on observe que 36+30=66% des années les plus chaudes se sont produit après 1930.

Réalisez le calcul pour positionner l’année peut s’avérer compliqué. On pourrait envisager de porter directement le pourcentage de temps restant sur la période d’étude.

ggplot(dat_)+aes(x=-prop_an,y=pr_an_c-prop_an)+
  geom_point()+
  scale_y_continuous(breaks=seq(0,0.3,.05),labels=scales::percent)+
  scale_x_continuous(breaks = seq(-1,0,0.1),labels=scales::percent)+
  theme_bw()+
  theme(axis.title= element_blank())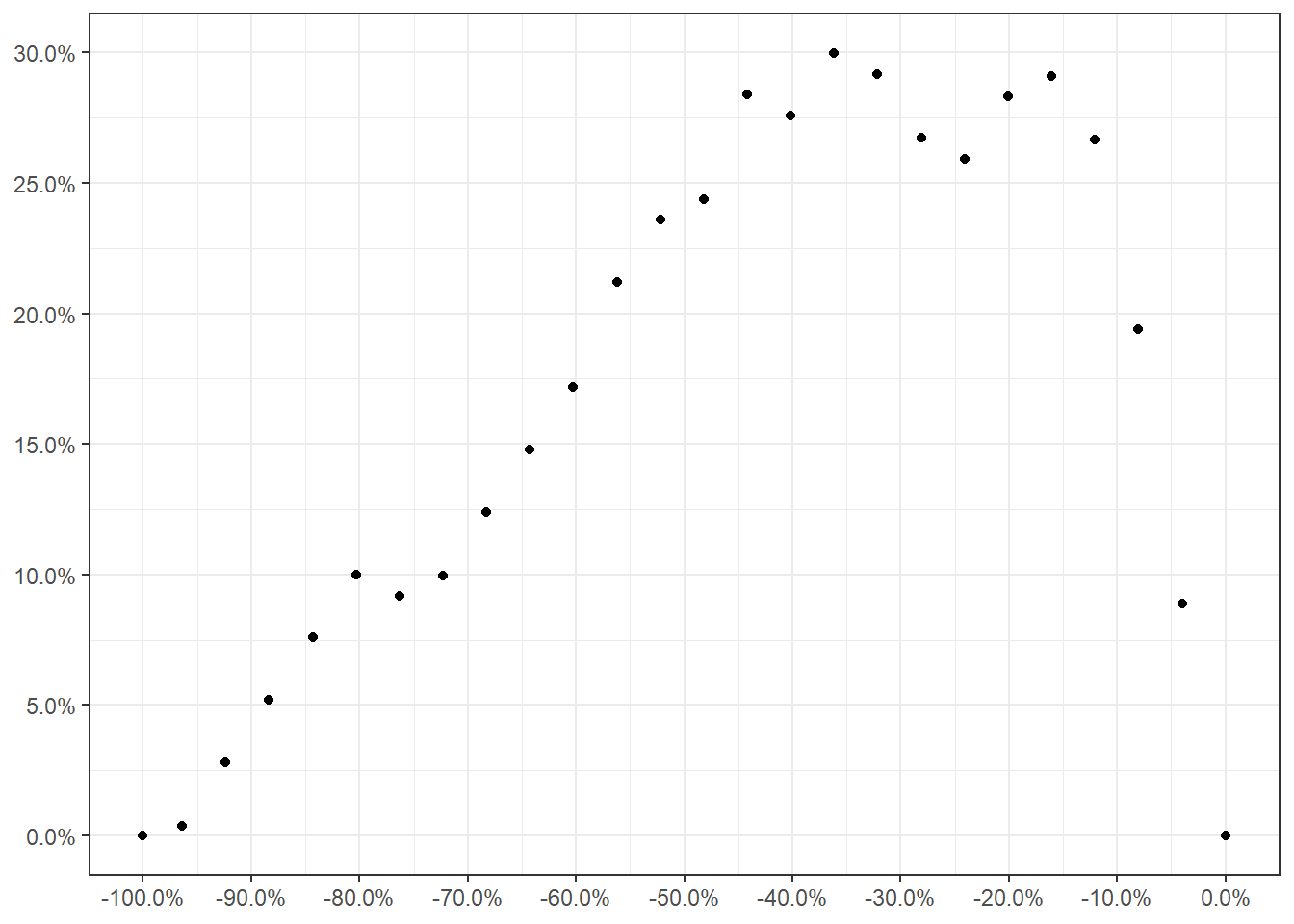

La lecture est plus facile mais on a encore une fois les choses ne sont pas parfaites. Quelque soit la représentation choisie, on voit bien que les années les plus chaudes se concentrent sur les dernières décennies.

Envisageons tout de même un autre type de graphe s’articulant autour de dénombrement. Essayons en nuage de points les fréquences cumulées des températures. Pour cela, établissons la proportion d’années présentant une température moyenne inférieure à celle de l’année considéré.

dat_1<-dat %>% mutate(prop_an_d_inf=(rank(deg_C)-1)/249) %>%
               select(annee,deg_C,prop_an_d_inf) %>% 
               arrange(annee)
head(dat_1)

## # A tibble: 6 x 3
##   annee deg_C prop_an_d_inf
##   <dbl> <dbl>         <dbl>
## 1  1772  9.17         0.367
## 2  1773  9.29         0.460
## 3  1774  9.08         0.295
## 4  1775 10.1          0.847
## 5  1776  9.01         0.245
## 6  1777  9.11         0.329

Retenons la température en abscisse et la proportion de d’années à température inférieure à elle en ordonnée. Ajoutons une couleur suivant une progression allant de l’année la plus éloignée à la plus proche. Utilisons celle nommée turbo du package viridis.

ggplot(dat_1) +
  geom_point(aes(deg_C,prop_an_d_inf,color=annee),shape=19,size=1.1)+
  geom_hline(yintercept = 0.75, linetype='dotted')+
  labs(x='°C')+
  scale_x_continuous(breaks=seq(7.25,11,0.25))+
  scale_y_continuous(labels=scales::percent)+
  scale_color_viridis(option="turbo")+
  guides(color=guide_colorbar(title="année",
                              title.position = 'top',
                              title.hjust=0.5,
                              barwidth=unit(20,'lines'),
                              barheight = unit(0.5,'lines')))+
  theme_bw()+
  theme(legend.position = 'top',
        axis.title.y = element_blank())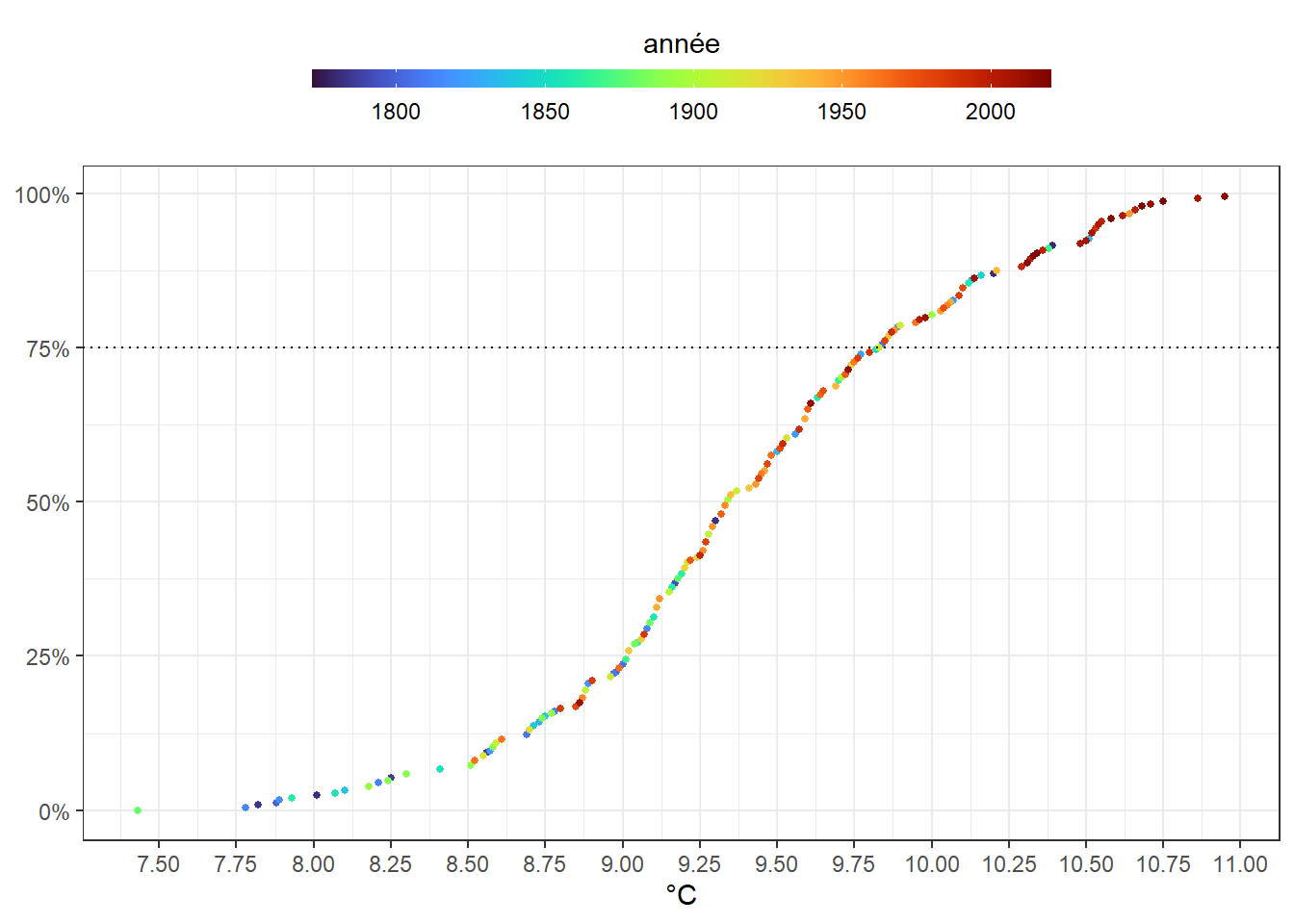

Marquons la température les plus chaudes, celles appartenant au dernier quartile des températures, par une ligne pointillée horizontale. On remarque que les points les plus rouges sont concentrées au-dessus de cette ligne. Encore une fois, cela met en évidence que les années les plus récentes sont aussi les plus chaudes.

travailler sur une distance à une période de références ?

Prenons les choses sous un angle nouveau. Construisons une représentation basé sur la comparaison avec une période de référence. Choisissons la période avant 1900. Établissons la différence par rapport à la température moyenne de cette période et travaillons à partir de là.

dat_2<-dat %>% mutate(moy_19=mean(deg_C[annee<1900]),
                      dist_19=deg_C-moy_19,
                      plus_ch_19=dist_19>0) %>% 
               select(annee,dist_19,plus_ch_19)
head(dat_2)

## # A tibble: 6 x 3
##   annee dist_19 plus_ch_19
##   <dbl>   <dbl> <lgl>     
## 1  1772  0.0331 TRUE      
## 2  1773  0.153  TRUE      
## 3  1774 -0.0569 FALSE     
## 4  1775  0.963  TRUE      
## 5  1776 -0.127  FALSE     
## 6  1777 -0.0269 FALSE

Nous pourrions utiliser les mêmes représentations que dans la première partie de ce post. Nous préférons, cependant, travailler sur des alternatives. Commençons par un lolipop chart (une graphe à sucette), un type de graphe proche de celui proposé à titre d’illustration sur le site du Hadley Center duquel nous avons tiré les données qui prend pour période de référence 1961-1990. Ajoutons un marqueur pour distinguer la période de référence de la suite une ligne verticale violette. Ajoutons une couleur aux points marquant les distances à la moyenne (rouge pour les années les plus chaudes et bleu pour les plus froides).

ggplot(dat_2,aes(annee,dist_19))+
  geom_point(aes(color=plus_ch_19),size=1.5)+
  geom_hline(yintercept = 0)+
  geom_vline(xintercept = 1900,color='purple')+
  geom_segment(aes(xend=annee, 
                   y=0, 
                   yend=dist_19))+
  labs(y='écart par rapport à la moyenne avant 1900 (en °C)')+
  coord_cartesian(xlim=c(1770,2023),ylim=c(-1.80,1.9),expand = FALSE)+
  scale_color_manual(values=c("blue", "red"))+
  scale_x_continuous(breaks=seq(1770,2025,20))+
  scale_y_continuous(breaks=seq(-2,2,0.25))+
  theme_bw()+
  theme(axis.title.x = element_blank(),
        legend.position = 'none',
        panel.grid.minor = element_blank())

On voit bien que sur la période de référence (avant 1900) les points rouges et les points bleus se répartissent uniformément au-dessus et en-dessous de la droite y=0. Sur la période post 1900, on voit que les points rouges sont bien plus nombreux que les points bleus ce qui une nouvelle fois marque le réchauffement.

Une représentation alternative du même genre pourrait se baser sur des aires à la place des sucettes. Pour cela, on utilise le geom_area(). Colorons en rouge les aires correspondant aux températures supérieures à la référence et en bleu les aires correspondant aux températures inférieures.

ggplot(dat_2,aes(annee,dist_19))+
  geom_area(aes(fill=plus_ch_19),colour='black')+
  geom_hline(yintercept = 0)+
  geom_vline(xintercept = 1900,color='purple')+
  labs(y='écart par rapport à la moyenne avant 1900 (en °C)')+
  coord_cartesian(xlim=c(1770,2023),ylim=c(-1.80,1.9),expand = FALSE)+
  scale_fill_manual(values=c("blue", "red"))+
  scale_x_continuous(breaks=seq(1770,2025,20))+
  scale_y_continuous(breaks=seq(-2,2,0.25))+
  theme_bw()+
  theme(axis.title.x = element_blank(),
        legend.position = 'none',
        panel.grid.minor = element_blank())

Avant 1900, l’aire au-dessus et en-dessous de la droite horizontale sont de même valeur. Après 1900, l’aire au-dessus est bien plus importante que l’aire en-dessous.

Envisageons une autre représentation basée cette fois sur une référence mobile. Commençons par marquer les températures sur des périodes d’un quart de siècle. Pour cela, utilisons pour ce faire la fonction cut().

dat <- dat %>% mutate(ving_5=cut(dat$annee,breaks=seq(1772,2025,25),
                                 include.lowest = TRUE,dig.lab = 4))

Ceci fait, présentons un nuage de points pour chaque quart de siècle. Assurons-nous que les points ne s’alignent pas sur une seule droite en utilisant position_jitter(). Afin d’ajouter un repaire visuel pour faciliter le repaire de tendance, superposons à l’ensemble des boîtes à moustaches.

ggplot(dat)+
  aes(ving_5,deg_C)+
  geom_boxplot(aes(color=ving_5),show.legend=FALSE)+
  geom_point(size=0.5,position=position_jitter(width=0.2,seed = 5))+
  labs(y='°C')+
  theme_bw()+
  theme(axis.title.x=element_blank(),
        axis.text.x = element_text(size=8),
        axis.title.y=element_text(angle=360,vjust=0.5))

On voit bien une tendance à la hausse à partir de 1872 et que le dernier quart de siècle est nettement le plus chaud.

l’inclusion d’autres marqueurs de tendance ?

Pour finir ce post déjà trop long, considérons des marqueurs de tendance plus fins que ceux utilisés dans le graphe de base. Commençons par utiliser une moyenne mobile (roulante). Disons sur 5 années. Il s’agit d’une valeur établie à chaque date en prenant les 5 dernières dates. Le package zoo propose une fonction dédiée rollmean().

dat<-dat %>% mutate(min_d_am5=zoo::rollmean(dat$deg_C,5,na.pad=TRUE))

Reprenons le nuage de points des températures et ajoutons-lui une courbe (verte) établie sur la base de la moyenne mobile calculée.

ggplot(dat)+
  aes(annee,deg_C)+
  geom_point()+
  geom_line(aes(y=min_d_am5),color='green')+
  coord_cartesian(xlim=c(1770,2022),
                  ylim=c(7.5,11),
                  expand=FALSE)+
  scale_x_continuous(breaks = seq(1770,2025,20))+
  scale_y_continuous(breaks = seq(8,12,0.5))+
  labs(y='écart par rapport au minimum')+
  theme_bw()+
  theme(axis.title.x=element_blank())

Encore une fois, on voit bien que la courbe suit une tendance clairement haussière à compter du début du vingtième siècle.

On peut utiliser le même marqueur de tendance sur notre lolipop chart. Calculons la moyenne mobile sur 5 années pour la distance à la moyenne des températures sur la période antérieure à 1900.

dat_2a<-dat_2 %>% mutate(min_d_am5=zoo::rollmean(dat_2$dist_19,5,na.pad=TRUE))

Prenons la couleur violette pour notre courbe de tendance.

ggplot(dat_2a,aes(annee,dist_19))+
  geom_point(aes(color=plus_ch_19),size=1.5)+
  geom_hline(yintercept = 0)+
  geom_vline(xintercept = 1900,color='purple')+
  geom_segment(aes(xend=annee, 
                   y=0, 
                   yend=dist_19))+
  geom_line(aes(y=min_d_am5),color='purple',size=.75)+
  labs(y='écart par rapport à la moyenne avant 1900 (en °C)')+
  coord_cartesian(xlim=c(1770,2023),
                  ylim=c(-1.80,1.9),
                  expand = FALSE)+
  scale_color_manual(values=c("blue", "red"))+
  scale_x_continuous(breaks=seq(1770,2025,20))+
  scale_y_continuous(breaks=seq(-2,2,0.25))+
  theme_bw()+
  theme(axis.title.x = element_blank(),
        legend.position = 'none',
        panel.grid.minor = element_blank())

## Warning: Removed 4 row(s) containing missing values (geom_path).

La moyenne mobile marque bien la tendance et elle est assez flexible. On l’utilise souvent pour désaisonnaliser une série temporelle. On peut faire varier le nombre de périodes retenues pour la moyenne mobile afin d’affiner la représentation. Ici, le choix de 5 ans est purement arbitraire. Une réflexion avancée sur ce paramètre qui appuyer ce choix.

Une autre possibilité pour mettre en évidence des tendances est de chercher les moyennes les plus représentatifs de périodes caractéristiques. On peut utiliser différents package associés à l’études des séries temporelles pour les déterminer. Ceux-ci reposent sur différentes stratégies (sur lesquelles nous reviendrons dans un prochain post). Choisissons le package tree qui réalise une classification hiérarchique.

library(tree)

## Registered S3 method overwritten by 'tree':
##   method     from
##   print.tree cli

tree_mod <- tree(deg_C ~ annee, data = dat)
plot(tree_mod)
text(tree_mod, pretty = TRUE)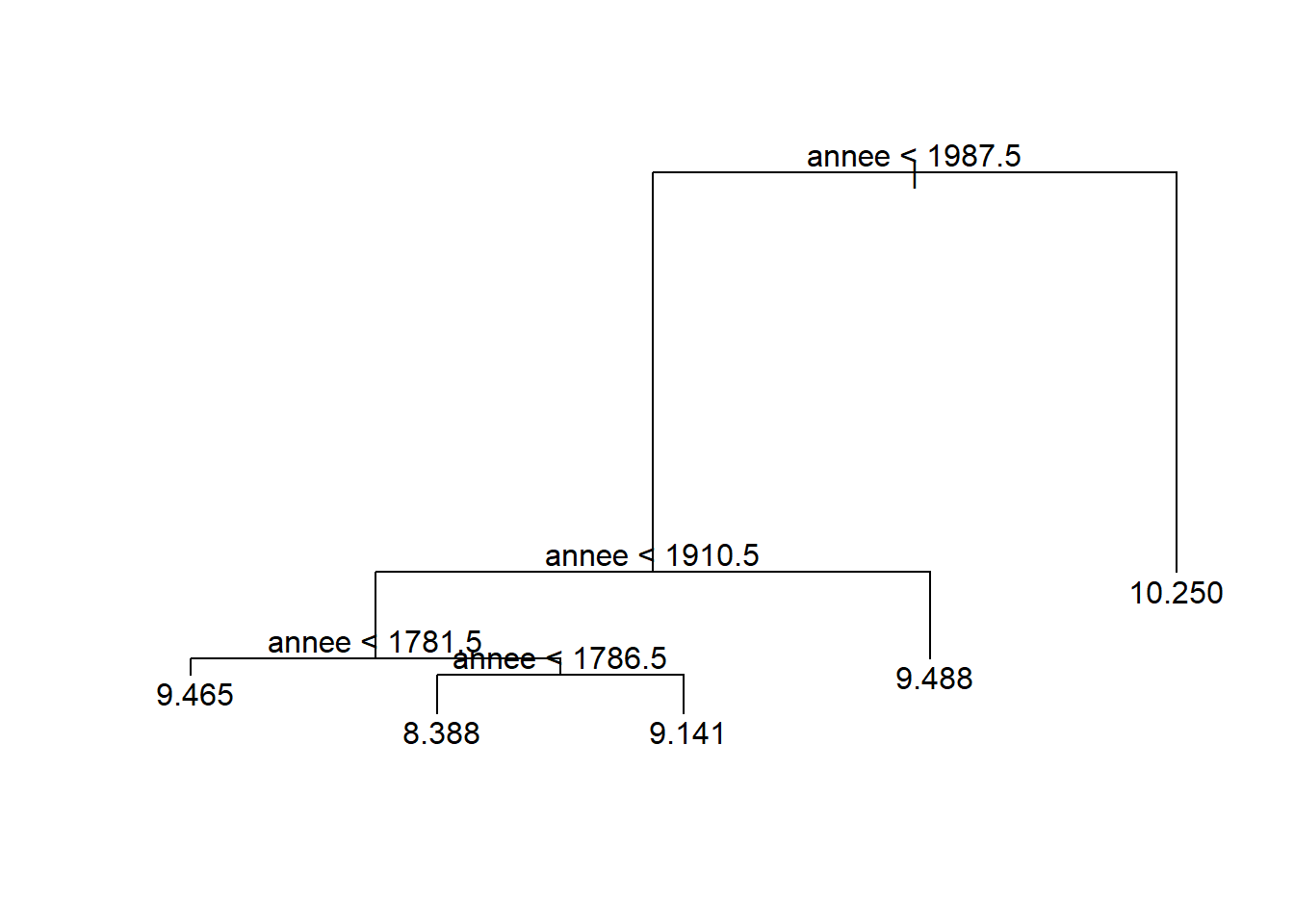

Limitons-nous à trois périodes : 1772-1910;1911-1987;1988-2020. Encore une fois, ici le choix est arbitraire. L’arbre identifie 5 périodes (1772-1781 avec 9.465; 1782-1786 avec 8.388; 1786-1910 avec 9.141; 1911-1987 avec 9.488; 1988-2020 avec 10.250). Coupons l’arbre en conséquence. Représentons les moyennes correspondant par des segments rouges ajouter à notre nuages de points des températures.

ggplot(dat)+
  aes(annee,deg_C)+
  geom_point()+
  geom_segment(aes(x=1988,
                   xend=2020, 
                   y=10.250, 
                   yend=10.250),color='red')+
  geom_segment(aes(x=1911,
                   xend=1987, 
                   y=9.488, 
                   yend=9.488),color='red')+
    geom_segment(aes(x=1772,
                   xend=1910, 
                   y=9.136739, 
                   yend=9.136739),color='red')+
  coord_cartesian(xlim=c(1770,2022),
                  ylim=c(7.5,11),
                  expand=FALSE)+
  scale_x_continuous(breaks = seq(1770,2025,20))+
  scale_y_continuous(breaks = seq(8,12,0.5))+
  labs(y='écart par rapport au minimum')+
  theme_bw()+
  theme(axis.title.x=element_blank())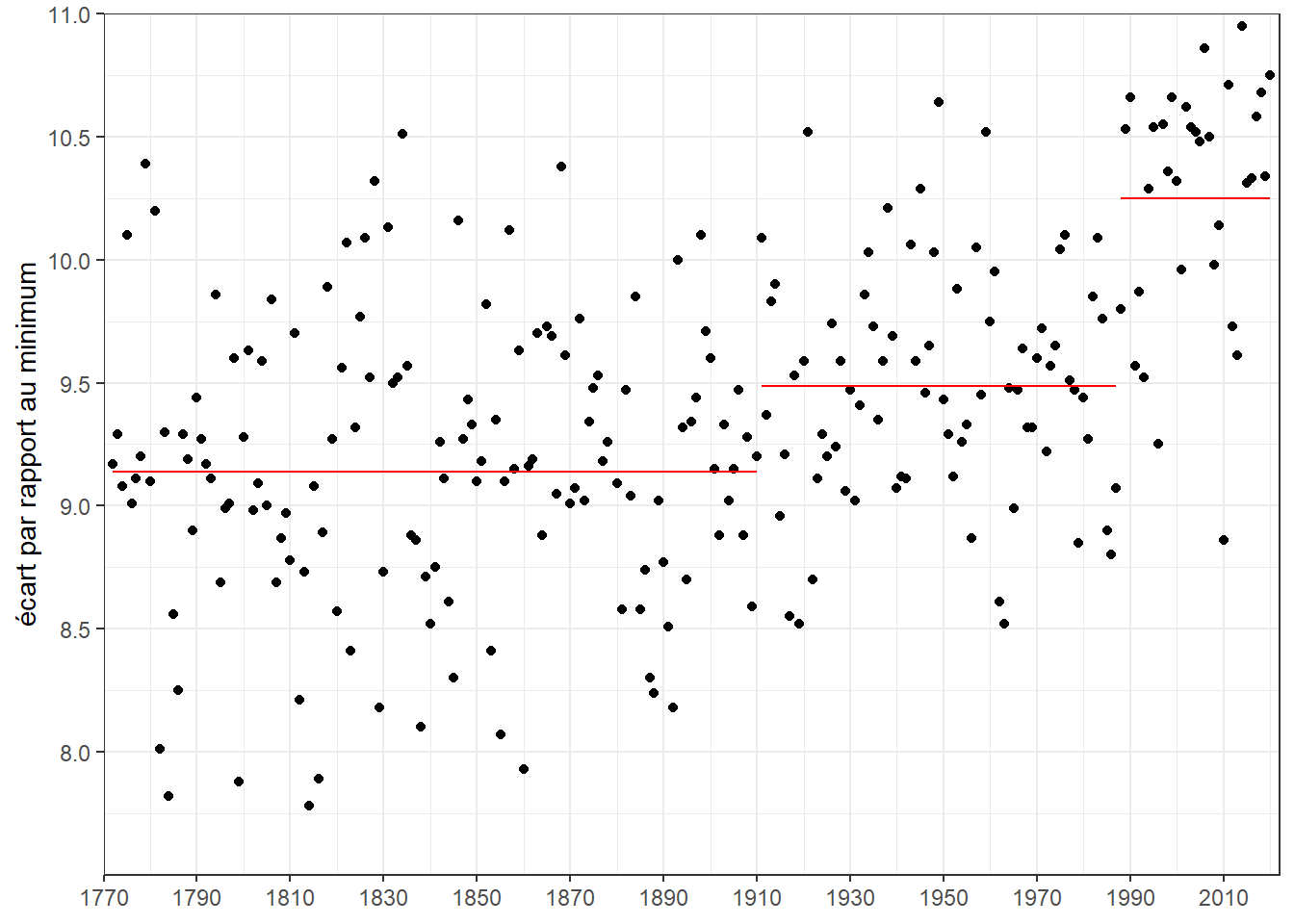

Une autre possibilité est non plus d’établir des moyennes représentatives pour différentes périodes mais des droites de régressions marquant des tendances périodiques. Le package segmented permet d’isoler les plus représentatives. Il procède par itération à partir de références proposées. Ici, retenons trois périodes. Pour ce faire, donnons-lui deux références à partir desquels commencer à travailler (1900 deux fois pour faire simple). Ici, n’importe quelle date (de la période d’étude) peut être retenue.

library(segmented)
df<-dat %>% select(deg_C,annee) %>% rename(y=deg_C,x=annee)
lin_mod <- lm(y ~ x, data = df)
segm_mod <- segmented(lin_mod, seg.Z = ~x,psi=list(x=c(1900,1990)))
summary(segm_mod)$psi

##        Initial     Est.   St.Err
## psi1.x    1900 1887.480 30.64849
## psi2.x    1990 1981.007 11.57363

Le choix du nombre de périodes est ici arbitraire. Dans le cadre d’un travail d’analyse, il devrait être justifié. Celles identifiées par l’algorithme sont: 1772-1887; 1888-1981; 1982-2020. Traçons le graphe reprenant les segments associés en mobilisant le geom_smooth() avec la méthode lm (modèle linéaire).

dat<-dat %>% mutate(g_p=ifelse(dat$annee<1887,'p1',ifelse(dat$annee<1981,'p2','p3')))
ggplot(dat)+
  aes(annee,deg_C,color=g_p)+
  geom_point()+
  labs(y='°C')+
  coord_cartesian(xlim=c(1770,2022),
                  ylim=c(7.25,11),
                  expand=FALSE)+
  scale_x_continuous(breaks=seq(1770,2025,20))+
  scale_y_continuous(breaks=seq(7,11,0.5))+
  geom_smooth(method = "lm", se = FALSE)+
  theme_bw()+
  theme(legend.position = 'none',
        axis.title.x = element_blank(),
        axis.title.y = element_text(vjust=0.5,angle=0))

## `geom_smooth()` using formula 'y ~ x'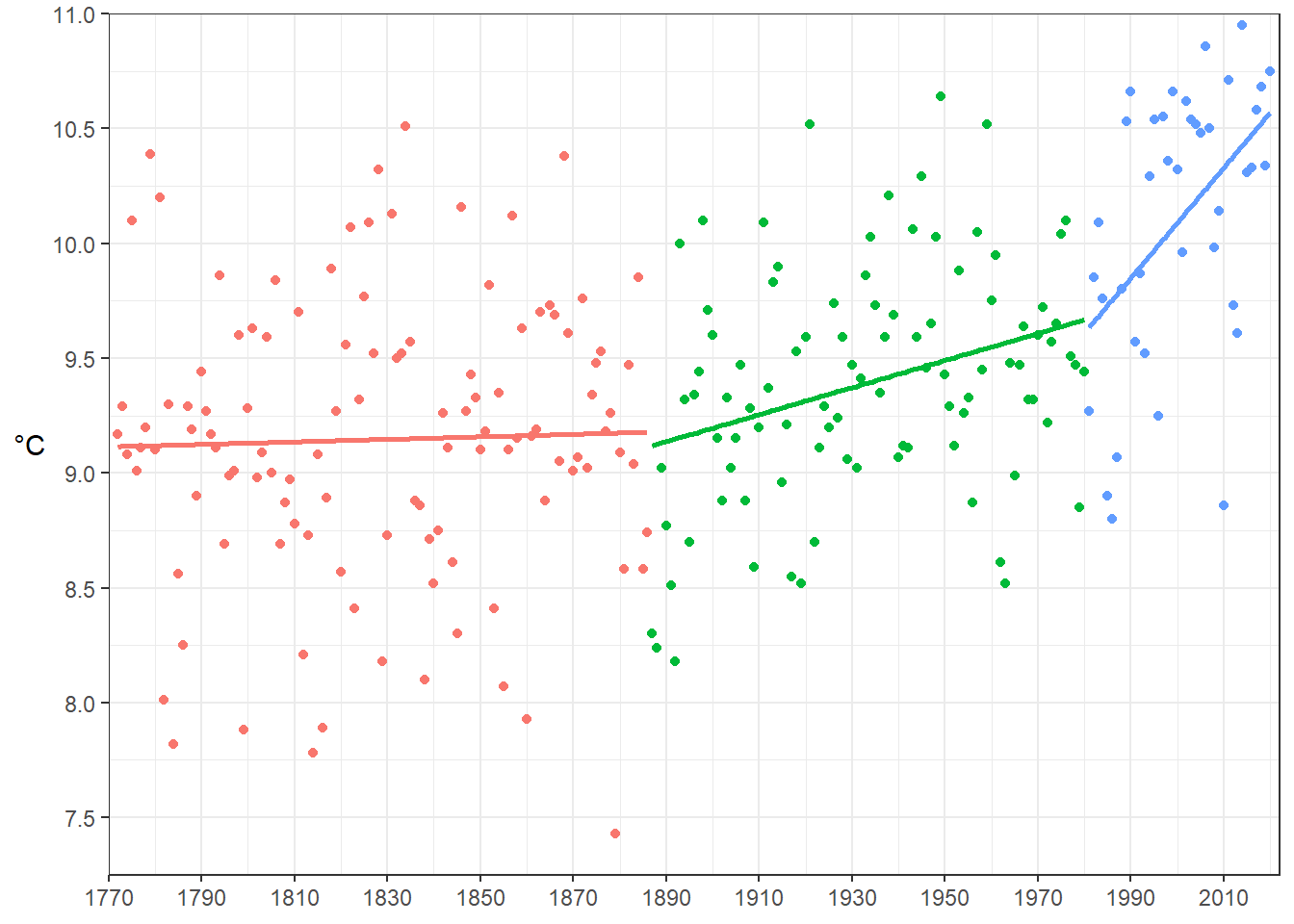

L’ensemble des stratégies graphiques présentées ici n’est qu’un aperçu de ce qu’il est possible de réaliser avec GGPLOT pour mettre en relief les tendances mises au jour dans les données travailler. On peut sans difficulté croisé ou approfondir ces méthodes pour renforcer le message et mieux communiquer les résultats d’analyse. Ici, les limites sont celles de votre créativité et de la rigueur qui s’impose pour un traitement honnête des faits. Rappelons, avant de clore, que tous les graphes produits peuvent être accompagnés de titres, sous-titres, légendes et autres textes qui en facilitent la compréhension. Même si nous avons négligé, dans une très large mesure, cette dimension sur ce post, ces éléments sont importants et doivent être travaillé avec autant de soin que le reste. Nous y reviendrons prochainement.