Dans ce nouveau post, nous allons faire un pas de coté et laisser pour un temps la question de l’estimation d’une diff-in-diff pour ne concentrer sur les tests de la parallel trend hypothesis. Rappelons-le, celle-ci fait référence au fait que l’évolution de l’outcome pour le groupe des traités aurait dû suivre une évolution parallèle à celles du groupe de contrôle en l’absence de traitement. Si c’est le cas, toute déviation vis-à-vis de cette trajectoire intervenant suite au traitement ne peut être causée que par celui-ci. Cette déviation est alors l’effet du traitement sur les traités. En l’absence de parallel trend la méthode diff-in-diff n’est pas en mesure d’identifier le lien causale entre le traitement et l’outcome. Il est donc important de convaincre de sa plausibilité et cela sachant qu’il est impossible de tester directement son existence. En effet, on ne peut, par définition, pas observer ce qui se serait passé en l’absence de traitement pour les traités après le traitement.
La stratégie généralement mise en place pour pallier à la difficulté consiste à tester l’existence de la parallel trend sur la période pré-traitement. Ce faisant, on fait l’hypothèse que, si celle-ci existe bien avant le traitement, elle aurait continué à exister, en absence de traitement, sur la période post-traitement. D’un point de vue pratique, on test l’existence d’une tendance linéaire (une pente) commune entre le groupe des traités (avant qu’ils le soient) et le groupe contrôle sur l’outcome sur la période pré-traitement (H0).
C’est ce que nous avons fait dans les posts précédents pour les réplications présentant suffisamment de données, autrement-dit, lorsque celles-ci ne se limitaient pas à deux temps d’observations, un avant et un après le traitement, et que nous avons pu en conséquence mettre en place une estimation en TWFE. L’analyse est pratiquée soit sur la base d’un test dédié (sous Stata estat ptrends), soit sur la base de la lecture de graphes particuliers (sous Stata estat trendsplots ou estat grangerplot). La seconde option est la plus courante dans sa variante exploitant les dynamic treatment effects, notamment quand l’étude prend la forme d’une event study.
Cette approche présente néanmoins des limites. Nous en examinerons ici deux ainsi que des solutions qui sont proposées pour les dépasser. Tout d’abord, elle peut avoir une puissance faible, autrement-dit elle peut échouer à détecter une violation de la parallel trend alors que cette violation est existe. Ensuite, elle conduit à ne considère que des cas où les tests confirme la présence d’une parallel trend linéaire sur la période traitement. Cela crée de fait une forme de biais de sélection quand au situation examinée. Nous excluons les situations le test rejette la parallel trend mais celle-ci serait au moins partiellement présente.
La puissance des tests de parallel trend
Jonathan Roth (2022) propose dans un papier de l’AER une méthode pour évaluer la puissance et les distorsions associées à la parallel trend. Le package pretrends permet de mettre en place cette méthode.
Pour mieux comprendre comment cette méthode fonctionne, reprenons l’exemple qu’il développe dans ses différentes présentations. Mais avant de commencer chargeons les packages qui nous seront utiles pour la suite.
# manipulation et chargement de données
library(tidyverse)
library(haven)
# estimation et test Diff in Diff et autres tests classiques
library(fixest)
library(lmtest)
library(sandwich)
library(car)
# visualisation données de panel
library(panelView)
# test de la parlléle trend
library(pretrends)
library(HonestDiD)Ceci étant fait. Intéressons-nous aux données. L’illustration du package est réalisée à partir de celles de He and Wang (2017) . Il ne reprend que les éléments associés à l’estimation d’un des modèles diff in diff du papier. Nous remontrons ici un peu plus loin de manière à extraire nous-même ces éléments.
Le replication pack pour cette étude est disponible sur la page correspondante de le AEJ. Nous n’avons pas besoin de l’ensemble des fichiers mis à disposition. Le seul dont nous avons besoin est nommé workfile_AEJ.dta . Il comprend les données nécessaires à la réplication de la plus part des tableaux et notamment celles permettant de répliquer la table 5. C’est à partir du premier modèle de cette table que nous travaillerons. Vous pouvez trouvez le fichier ici. Une fois le fichier obtenu et placé dans notre environnement de travail, il ne reste plus qu’à charger la base dans R en utilisant read_dta() du package haven.
dat_<- read_dta("data/workfile_AEJ.dta")Avant d’aller plus loin, rappelons ce que réalise l’étude. Elle s’intéresse aux effets sur les programme de réduction de la pauvreté d’une politique mises en place en Chine visant à améliorer la qualité bureaucratique au niveau local en affectant des diplômés des universités à l’administration de villages. La politique est nommé CGVO (College Graduate Village Officials). Les diplômés n’étant pas affectés à tous les villages ni même affectés au même moment, l’étude établie l’effet de la politique à partir d’une diff-in-diff. La période étudiée cours de 2000 à 2011 et elle concerne 255 villages. L’étude met en évidence que la politique améliore le ciblage et la mise en oeuvre des programmes gouvernementaux d’assistance sociale. Elle donne également des éléments quant aux mécanismes à l’œuvre.
Ici, nous nous limiterons à l’impact du CGVO sur le taux de subventions accordées (le log de ce taux, l_subsidy_rate, pour être plus précis). Limitons la base aux seuls éléments dont nous avons besoins et procédons à quelques mises en formes pour faciliter la suite (création de variable pour les effets fixes et suppression des observations comprenant des valeurs manquantes pour l’outcome).
dat_r<-dat_ %>%
select(l_subsidy_rate,cgvo,v_id,year) %>%
mutate(village=as.character(v_id),
annee=as.character(year)) %>%
filter(!is.na(l_subsidy_rate))Ceci fait, voyons ce que l’on a. Pour cela, utilisons la fonction panelview() du package éponyme. Ajustons légèrement la fenêtre de rendu afin de pouvoir mieux visualiser l’ensemble (on passe ici à 10 sur 10).
panelview(l_subsidy_rate ~ cgvo ,
data = dat_r, index = c("village","annee"),
xlab = "année", ylab = "village",type='treat',
legend.labs = c("hors traitement", "traité (cgvo)",
"non observé"),
main="structure du panel au regard du traitement")## Specified labels in the order of: Under Control, Under Treatment, Missing.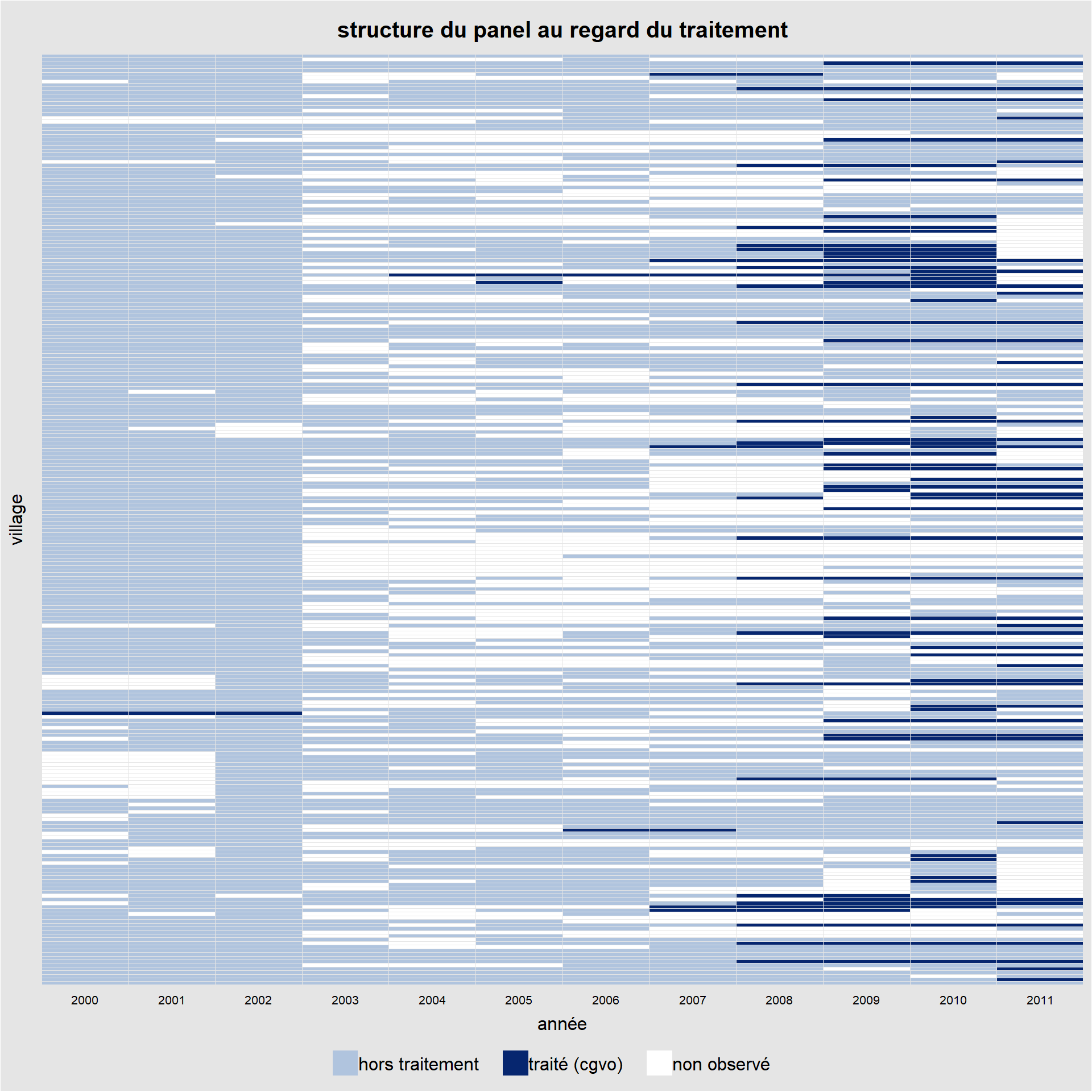
La lecture du graphe montre plusieurs choses. Tout d’abord, nous avons de nombreuses années pour lesquels nous n’avons pas d’observations. Ensuite, le traitement n’intervient qu’une fois par village, mais pas à la même date. De plus, la durée du traitement est également assez différente d’un village à l’autre. Enfin, il y a des villages qui voient leur statut de traité repassé à non traité après une période. Bref, on est loin d’un panel cylindré et d’un traitement homogène. Mais continuons. Comptons le nombre de villages traités et le nombre de villages qui ne le seront jamais sur la période d’étude (le groupe de contrôle).
dat_r %>%
group_by(village) %>%
summarise(vt=max(cgvo)) %>%
count(vt)## # A tibble: 2 × 2
## vt n
## <dbl> <int>
## 1 0 178
## 2 1 77On a 77 villages qui ont le statuts de traité au moins une fois sur la période (30% des villages étudiés) et 178 qui n’ont jamais eu ce statut (70%).
Mais, laissons ces éléments de côté pour procéder à l’estimation de notre diff-in-diff en TWFE. Comme d’habitude, nous utilisons la fonction feols() du package fixest pour la régression et coeftest() du package lmtest pour les tests sur le coefficient d’intérêt. Pour ce faire, nous mobilisons vcovCL() de sandwich afin de considéré un clustering au niveau des villages. Dans le papier d’origine, les auteurs test trois niveaux de clustering différents. Nous nous limiterons à celui-ci.
reg_did <- feols(l_subsidy_rate ~ cgvo |
village + annee,
data = dat_r)
coeftest(reg_did,vcov.=vcovCL(reg_did,cluster=dat_r$village))%>%
round(digits = 7)##
## t test of coefficients:
##
## Estimate Std. Error t value Pr(>|t|)
## cgvo 0.194173 0.086255 2.2512 0.02449 *
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1La régression permet de montrer un effet positif et statistiquement significatif au seuil de 5% du traitement sur l’outcome (le log du nombre de subventions). On retrouve le résultat présenté dans la première colonne de la table 5 du papier (la standard error avec cluster sur les villages est la seconde).
Voilà, mais venons en à ce qui nous intéresse : le test de l’hypothèse de parallel trend (colonne 1 de la table 6) notamment via le Granger plot comme réalisé dans le papier (Panel A de la figure 2). Il s’agit ici d’estimer la dynamique du traitement en utilisant une spécification basée sur l’interaction d’une variable marquant l’appartenance au groupe des traités et une série de variable binaire marquant chacune les périodes dans laquelle le traitement serait fictivement affecté. Ces périodes sont établies en temps d’évènement. Celles retenues sont quatre ans et plus avant (la réelle affectation du traitement), trois ans avant, deux ans avant, l’année de l’évènement, un an après, deux ans après, trois ans après. La période de référence est donc un an avant l’affectation réelle du traitement (ce qui est la configuration classique). On a ainsi le modèle suivant à estimer:
outcomei,t=γi+γt+K=3∑k≥−4;k≠1βk.Traité.Tk+ϵi,t
Où i correspond au village, t à l’année et k à la période d’affectation fictive du traitement.
On a ainsi, en plus des effets fixes, un jeu de variables binaires construites à partir des interactions. Pour les jamais traitées, elles ont toujours la valeur 0 puisque pour elles Traité, la variable indiquant si le village fait partie du groupe des traités, est égale à 0. Pour les traités, elles sont égales à 1 si l’observation considérée se situe dans la période désignée et 0 dans la cas contraire.
La base que nous avons chargée contient déjà ces variables codées de manière adéquate (Lead_D4_plus, Lead_D3, Lead_D2, D0, Lag_D1, Lag_D2, Lag_D3_plus). Nous les modifions légèrement pour nous assurer qu’elles soient introduites dans l’ordre sur le Granger plot. Ceci fait, procédons à l’estimation du modèle ainsi qu’aux tests d’inférences associés en retenant un clustering au niveau des villages.
dat_r_c<-dat_ %>%
filter(!is.na(l_subsidy_rate)) %>%
rename(aLead_D4_plus = "Lead_D4_plus",
bLead_D3="Lead_D3",
cLead_D2="Lead_D2",
dD0="D0",
eLag_D1="Lag_D1",
fLag_D2="Lag_D2",
gLag_D3_plus="Lag_D3_plus")
reg_dyn <- feols(l_subsidy_rate~aLead_D4_plus+bLead_D3+cLead_D2+
dD0+
eLag_D1+fLag_D2+gLag_D3_plus|
v_id + year,
data = dat_r_c)
coeftest(reg_dyn,vcov.=vcovCL(reg_dyn,cluster=dat_r_c$v_id))%>%
round(digits = 7)##
## t test of coefficients:
##
## Estimate Std. Error t value Pr(>|t|)
## aLead_D4_plus -0.089429 0.114100 -0.7838 0.43327
## bLead_D3 -0.089392 0.095029 -0.9407 0.34700
## cLead_D2 -0.068604 0.072417 -0.9473 0.34359
## dD0 0.093080 0.069929 1.3311 0.18333
## eLag_D1 0.187747 0.094955 1.9772 0.04817 *
## fLag_D2 0.180680 0.100094 1.8051 0.07122 .
## gLag_D3_plus 0.097278 0.146451 0.6642 0.50662
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1On retrouve bien les mêmes résultats que ceux produits dans la colonne 1 de la table 6 du papier.
Maintenant que nous avons estimé la dynamique du traitement, nous pouvons créer le Granger plot en retenant un intervalle de confiance à 95% pour les différents coefficients portant sur le traitement pour les différentes périodes retenues. Pour cela, utilisons ggcoef() du package GGally.
gr_1<-GGally::ggcoef(reg_dyn,
errorbar_height = 0.15,
errorbar_size = 1,
vline_linetype = "dashed",
vline_color = "black",
vline_size = 0.2)+
geom_hline(yintercept = 3.5,linetype="dashed")+
annotate(geom="point",x=0,y=3.5)+
labs(title="Effet dynamique du traitement",
subtitle = "intervalle de confiance à 95%",
x="Estimation DiD ",
y="Années-temps d'événement")+
scale_y_discrete(labels=c("-4 et plus","-3","-2","0","+1","+2","+3 et plus"))+
coord_flip()+
theme_minimal()+
theme(
plot.title = element_text(hjust = 0.5,face="bold"),
plot.subtitle = element_text(hjust = 0.5,face="italic"),
axis.line = element_line(color="black",linewidth=0.15),
axis.ticks = element_line(color="black",linewidth=0.1),
panel.grid.minor = element_blank())## Registered S3 method overwritten by 'GGally':
## method from
## +.gg ggplot2gr_1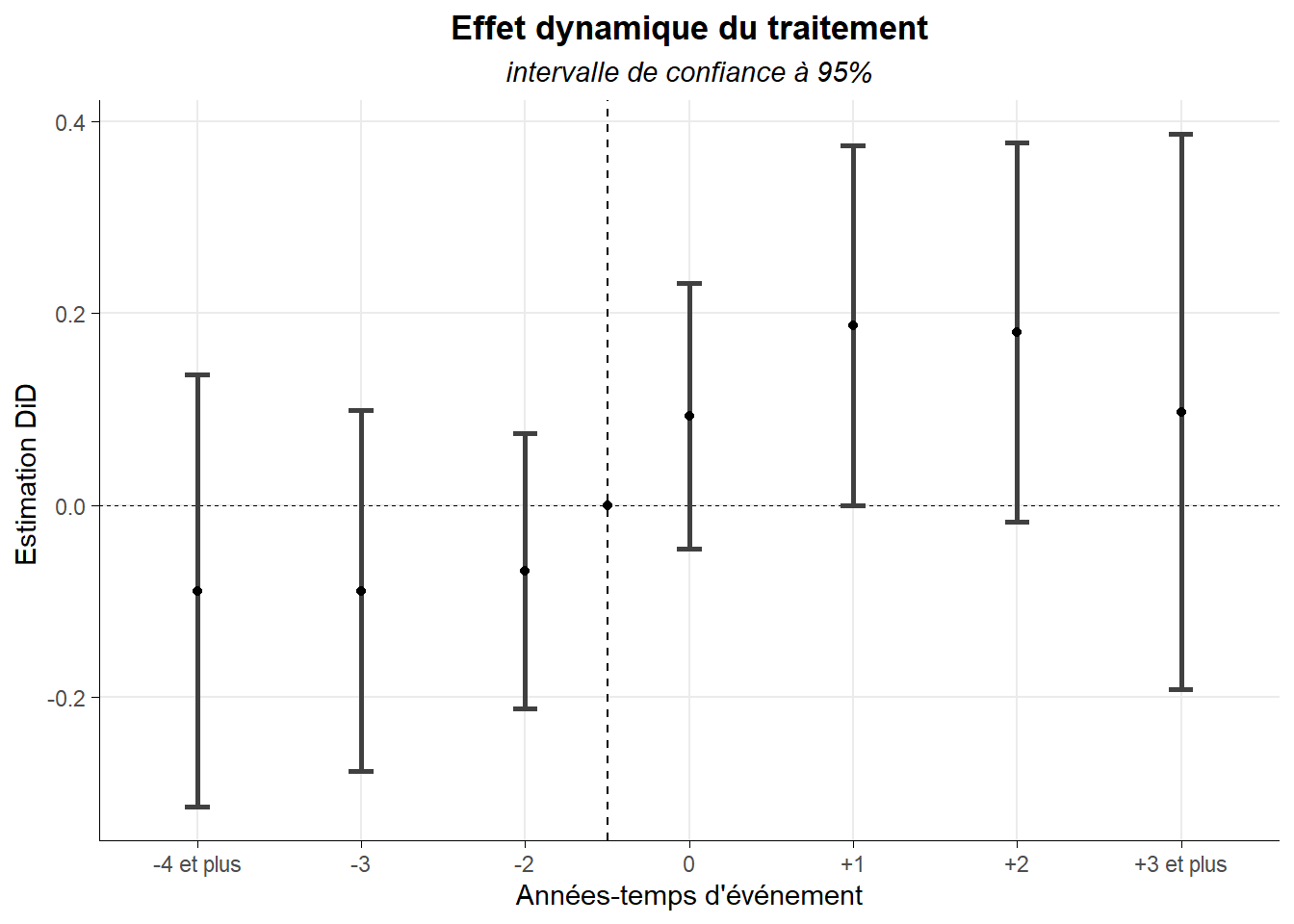
On retrouve le graphe présenté en panel A. Les auteurs indiquent que sa forme confirme l’hypothèse de parallel trend sur la période pré-traitement dans la mesure où les intervalles de confiance (à 95%) pour ces périodes comprennent la valeur 0. Cela peut être rapidement confirmer par un test portant sur les trois coefficients concernés (H0: ces trois coefficients sont égaux à 0). Faisons-le directement sans reconfigurer les variables pour suivre la procédure type estat granger de stata.
linearHypothesis(reg_dyn,c("aLead_D4_plus = 0",
"bLead_D3 = 0",
"cLead_D2 = 0"),
test="F",
vcov.=vcovCL(reg_dyn,cluster=dat_r_c$v_id),
white.adjust="hc1")##
## Linear hypothesis test:
## aLead_D4_plus = 0
## bLead_D3 = 0
## cLead_D2 = 0
##
## Model 1: restricted model
## Model 2: l_subsidy_rate ~ aLead_D4_plus + bLead_D3 + cLead_D2 + dD0 +
## eLag_D1 + fLag_D2 + gLag_D3_plus | v_id + year
##
## Note: Coefficient covariance matrix supplied.
##
## Res.Df Df F Pr(>F)
## 1 1832
## 2 1829 3 0.3722 0.7731Avec une p-value de 77,3%, on ne peut pas rejeter H0. Cela va dans le sens de la parallel trend dans le contexte pré-traitement.
Venons en au fond et au raisonnement de Roth. Le test sur les coefficients associés aux périodes pré-traitements pratiqué postule (sous H0) que les coefficients seraient alignés à la manière des points verts sur la figure ci-contre (qu’il n’y ai pas de différences de pentes entre le groupe de traité et le groupe de contrôle - les non-traités- sur la période pré-traitement).
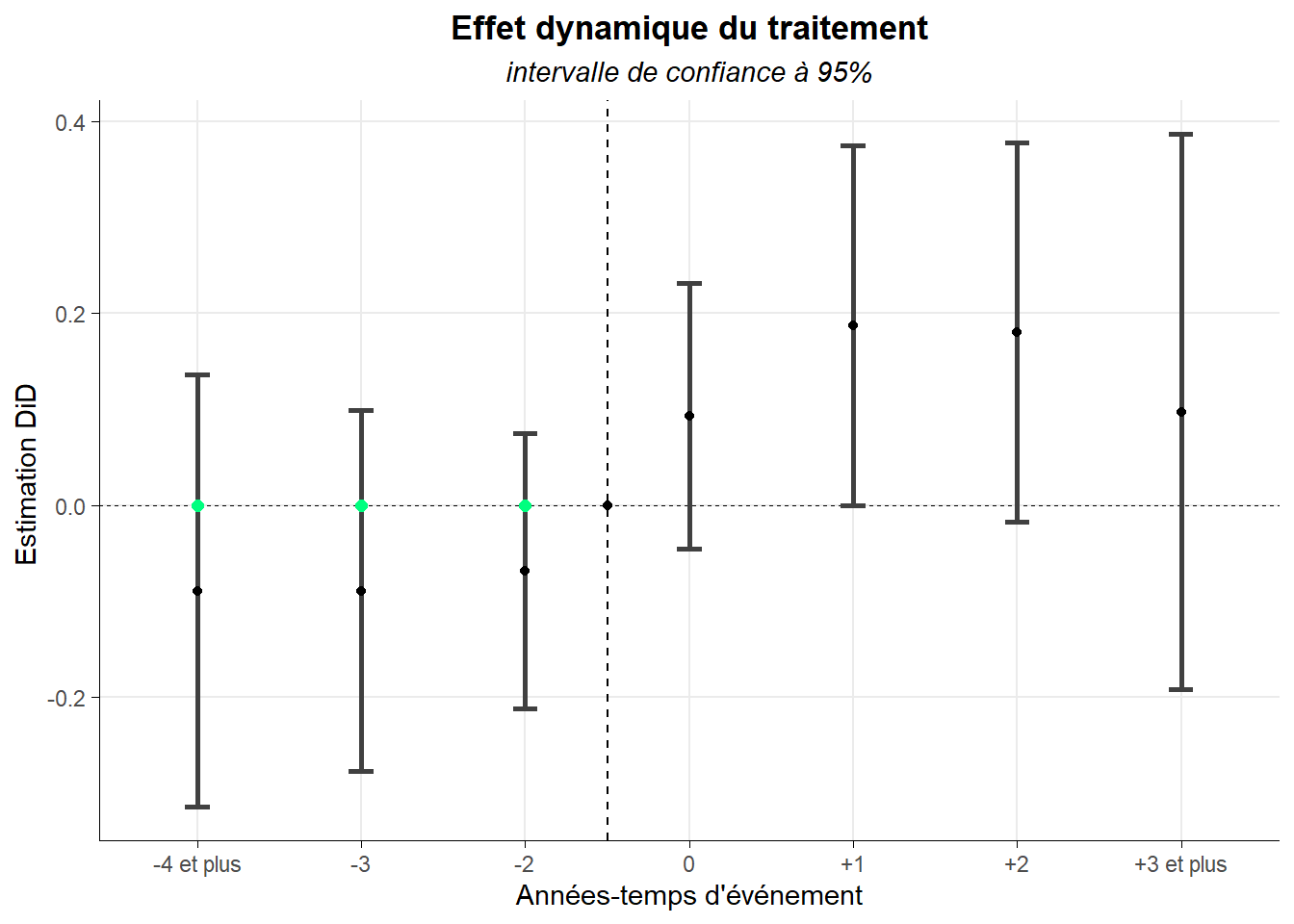
Néanmoins, le test considère comme suffisamment proche de cette situation toutes séries de trois points (un par période) situés à l’intérieur des intervalles de confiance. C’est le cas, dans la figure ci-dessous pour les séries de points rouges et bleus qui correspondent tous à des violations de la parallel trend (pré-traitement).
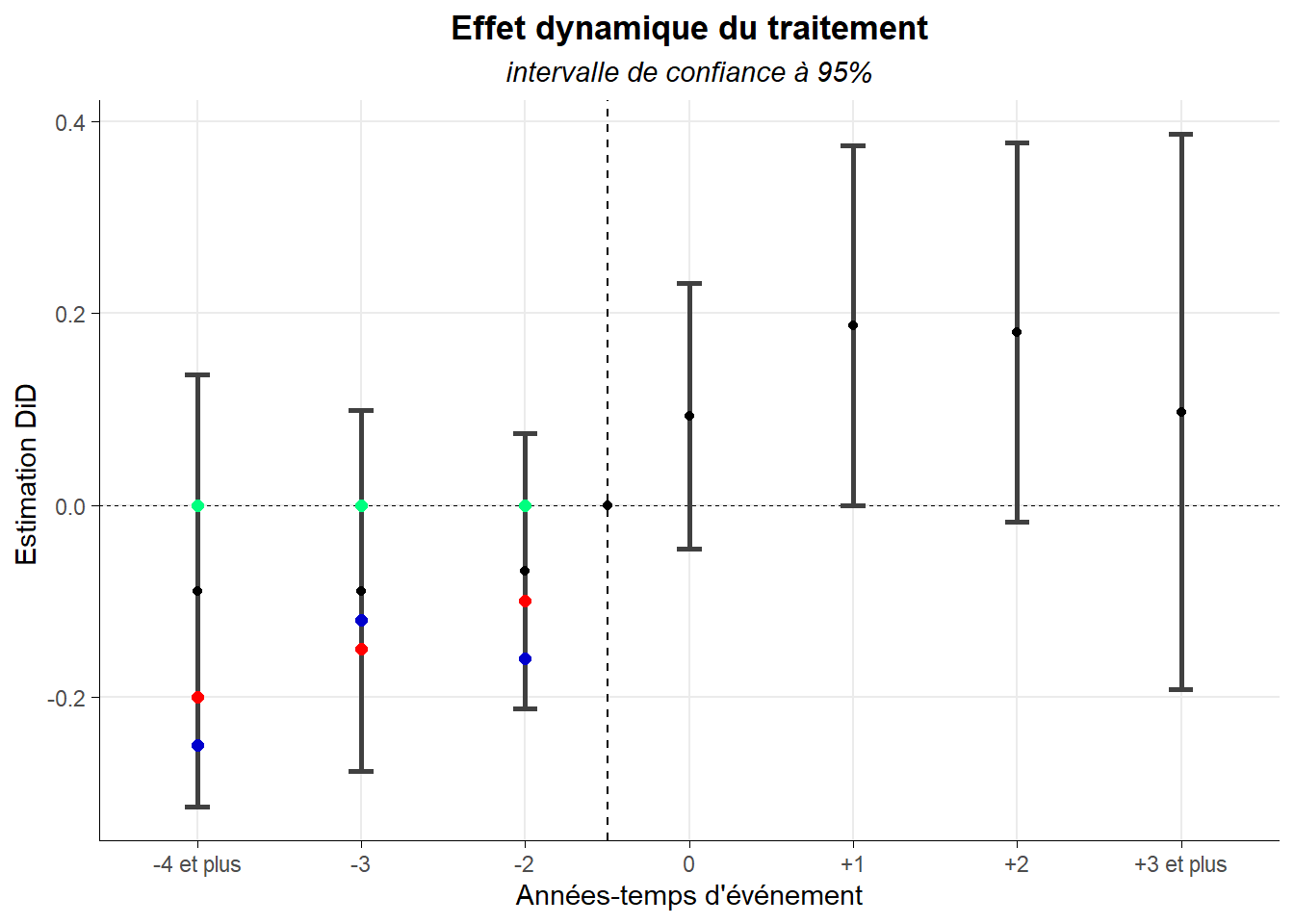
Les points rouges indiquent une tendance des valeurs de l’outcome des traités et des non traités à se rapprocher sur la période pré-traitement. Les points bleus indiquent que les valeurs se rapprochent puis s’éloignent sur la même période.
Or, dans les deux cas, les tests classiques (graphique ou plus formel) ne sont pas en mesure détecter ce type de situation. Ils manquent de puissance. Roth recommande pour compléter l’analyse de la pretrend d’éléments concernant la puissance du test réalisé. Pour cela, il propose une approche ex ante qui consiste à se poser la question de savoir de quelle amplitude devrait être la violation de la parallel trend pour que notre test classique soit à même de la détecter avec une probabilité donnée (par exemple 8 fois sur 10). On est ici proche de l’effet minimum détectable que l’on peut retrouver dans les expérimentations aléatoires classiques pratiqués en laboratoire (RCT).
Roth a développé le package pretrends pour automatiser le calcule. La fonction slope_for_power() renvoie l’amplitude de la violation minimal détectable pour le niveau de puissance désigné en input. Cette amplitude prend la forme d’une pente. Celle de la droite reliant la première série de points discordants avec la parallel trend qu’il est possible de détecter avec le test classique.
Les arguments de la fonction sont, outre le niveau de puissance choisi, des éléments du test de parallel trend classique via la dynamique de l’effet du traitement. On a aussi un vecteur comprenant les coefficients du modèle estimé pour le test, la matrice variance-covariance de ces estimations, un vecteur numérique reprenant le timing et l’indication de la période de référence. Reprenons tous cela dans des variables dédiées.
betas<-reg_dyn$coefficients
mat_cov<-reg_dyn$cov.iid %>% unname()
timing<-c(-4,-3,-2,0,1,2,3)
ref<- -1Injectons l’ensemble dans la fonction en optant pour une puissance de 80%, autrement-dit nous cherchons la violation la plus petite qui serait détecté par le test classique 8 fois sur 10.
slope_for_power(sigma = mat_cov,
targetPower = 0.8,
tVec = timing,
referencePeriod = ref)## [1] 0.085033Cette distorsion (minimum détectable) correspond à la pente de la droite liant les points situés (à la manière des rouges sur la figure précédente) sur les intervalles de confiance de la période pré-traitement. Cette droite présente pour chaque période défini les valeur suivante et 0 pour la période de référence.
0.08503895 * (timing - ref)## [1] -0.25511685 -0.17007790 -0.08503895 0.08503895 0.17007790 0.25511685
## [7] 0.34015580La fonction pretrends() propose des éléments d’interprétation et d’illustration de la situation mise en avant. Appliquons-la à nos données.
pretrends_res <- pretrends(betahat = betas,
sigma = mat_cov,
tVec = timing,
referencePeriod = ref,
deltatrue = 0.08503895 * (timing - ref))Parmi ces éléments, on retrouve un graphe présentant les intervalles de confiance de la dynamique de l’effet et la droit présentant la violation détectable la plus petite possible pour la puissance désirée (ici 80%). Le graphe, nommé event_plot, est au format ggplot. On peut donc procéder assez facilement à des mises en forme pour en améliorer le rendu. Voyons ce que cela donne.
pretrends_res$event_plot+
geom_hline(yintercept = 0,linetype="dashed")+
scale_x_continuous(breaks = -4:3,
labels = c("-4 et plus","-3","-2","1","0","+1","+2","+3 et plus"))+
theme_minimal()+
theme(
plot.title = element_text(hjust=0.5),
axis.title.x = element_blank(),
axis.line = element_line(color="black",linewidth=0.15),
axis.ticks = element_line(color="black",linewidth=0.1),
panel.grid.minor = element_blank(),
legend.position = 'top')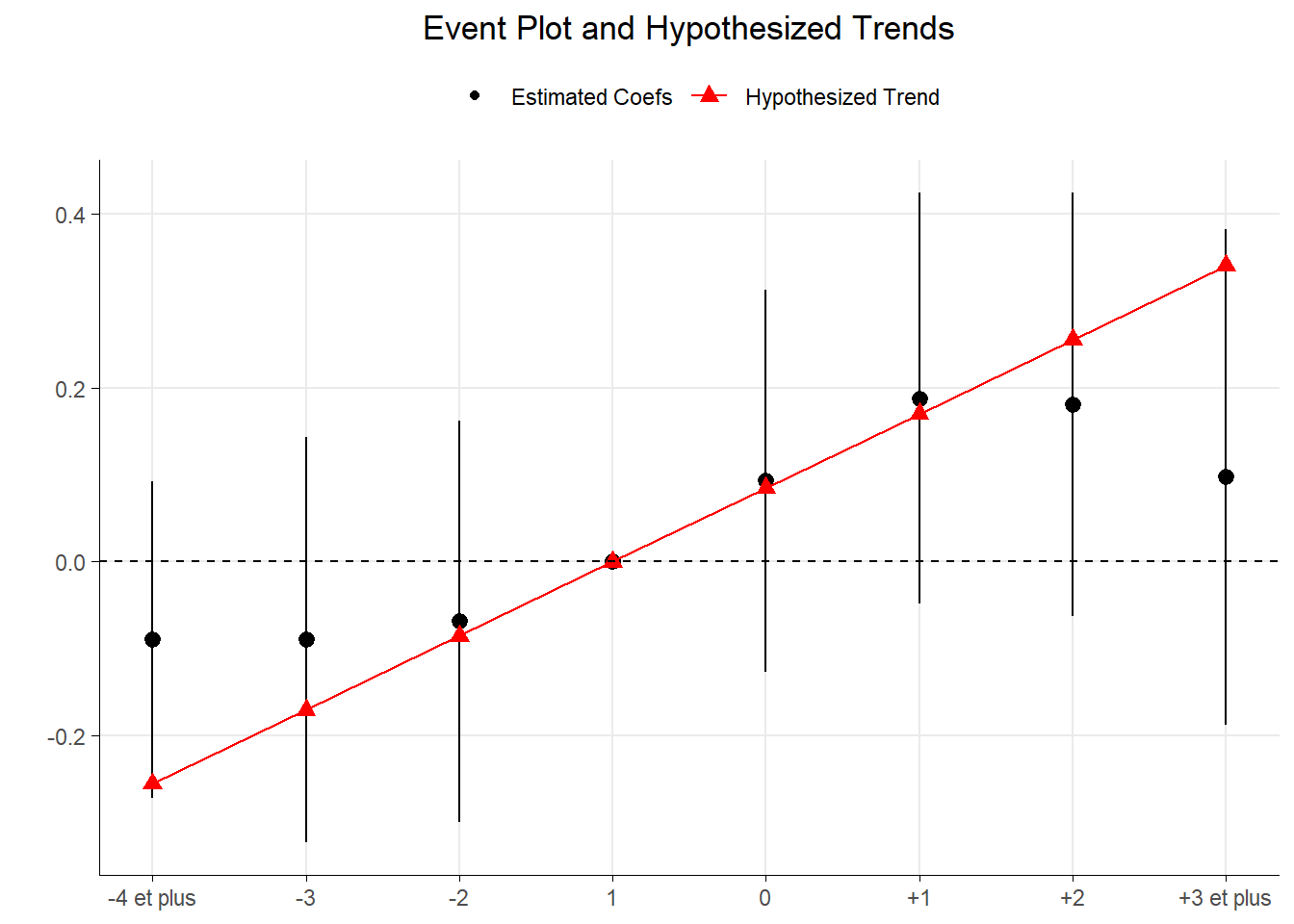
Un autre élément disponible intéressant est composé de trois statistiques exprimant à leur manière la puissance du test. Il est nommé df_power. Appelons-le et procédons à l’interprétation des informations fournies.
pretrends_res$df_power## Power Bayes.Factor Likelihood.Ratio
## 1 0.8001419 0.2267783 0.1442778La première statistique est la puissance du test de parallel trend classique. Nous l’avons fixé à 80%. Il s’agit de la probabilité de rejeter H0, la présence d’une parallel trend, si H1, son absence, est vraie. Dans le cas d’espèce, il y a une probabilité de 80% de détecter une violation de la parallel trend correspondant à une pente de 0,085 pour une droite qui lierait les intervalles de confiance sur le Granger plot.
La second statistique, le facteur de Bayes, indique les chances relatives que le test détecte une violation de la parallel trend si la tendance hypothétique, H1 (une tendance linéaire avec une pente de 0,085), est vraie, contre celle qu’il la détecte si la parallel trend, H0 (la pente est de 0), est vraie. Il compare ainsi la précision avec laquelle chaque hypothèse prédit les données observées. Une valeur inférieure à 1 permet de pencher en faveur de H0 tandis qu’une valeur supérieure à 1 amène à pencher pour H1. Ici, il est de 0,227 ce qui va dans le sens de la parallel trend mais modérément.
La troisième statistique, le ratio de vraisemblance, correspond à la mise en regarde de la vraisemblance du fait d’observer les coefficients du test classique si H1 est vraie et la situation correspond à la tendance théorisée (ici une pente de 0,085), et de la vraisemblance du fait d’observer ces coefficients si H0 est vraie, autrement-dit si la parallel trend est vraie. Le ratio est de 0,14 ce qui une nouvelle fois va dans le sens de la parallel trend.
Le biais de sélection des cas étudiés
Examinons maintenant la seconde difficulté. Celle associée au fait que les tests de parallel trend basés que la période pré-traitement conduisent à écarter certaines situations pouvant s’avérer dignes d’intérêt. En ne retenant pour l’analyse que les cas où ces tests n’excluent pas la parallel trend (pré-traitement), on créé une forme de biais de sélection quant au les résultats produits.
Pour palier à la difficulté, Rambachan and Roth (2023) proposent de réaliser une étude de sensibilité du résultat à la violation de la parallel trend. Prenons, pour illustrer cela, un des exemples mis en avant dans ce papier: l’un des résultats de l’étude de Benzarti and Carloni (2019).
Cette étude s’intéresse aux effets d’une forte baisse de la TVA sur la restauration en France mise en oeuvre en juillet 2009. Elle est alors passée de 19,5% à 5,5%. L’étude montre notamment que les bénéfices associées à cette baisse de taxe profites principalement aux propriétaires des restaurants (très peu aux consommateurs et pas du tout aux salariés).
Le résultat qui va nous intéresser ici est celui présenté dans la table 2 à la colonne 5. Il s’agit de l’impact du changement réglementaire sur le résultat des entreprises. Celui-ci correspond à une augmentation de 24% mesurée via une estimation diff-in-diff en TWFE à partir d’un groupe de contrôle constitué d’entreprises d’entreprises du secteur des services non affectées par la baisse de TVA. Ce résultat, comme les autres, est suivi de tests de robustesse de type de dynamic traitement effect illustré par un Granger plot. On retrouve le graphe associé dans la figure 2 panel E.
Ce sera notre point de départ. Dans la mesure où les données associées à l’ensemble sont difficilement disponibles, elles sont issues de la base Amadeus distribuée par le bureau Van Dyck, nous ne referons pas toute l’analyse. Nous nous rabattrons sur les éléments mis à disposition via le package HonestDiD. On y trouve directement des éléments issus de l’estimation de la diff-in-diff (estimation des bêtas, matrice variance-covariance de l’estimation, timing…). Utilisons la fonction data() pour y accéder.
data("BCdata_EventStudy",package="HonestDiD")
BCdata_EventStudy## $betahat
## [1] 0.006696352 0.029345034 -0.006472972 0.073014989 0.195961118
## [6] 0.312063903 0.239541546 0.126042500
##
## $sigma
## [,1] [,2] [,3] [,4] [,5]
## [1,] 8.428358e-04 4.768687e-04 2.618051e-04 0.0002354220 0.0001676371
## [2,] 4.768687e-04 6.425420e-04 3.987425e-04 0.0002435515 0.0002201960
## [3,] 2.618051e-04 3.987425e-04 5.229950e-04 0.0002117686 0.0001840722
## [4,] 2.354220e-04 2.435515e-04 2.117686e-04 0.0003089595 0.0001197866
## [5,] 1.676371e-04 2.201960e-04 1.840722e-04 0.0001197866 0.0003599704
## [6,] 1.128708e-04 1.804591e-04 1.458528e-04 0.0001334081 0.0002478819
## [7,] 1.992816e-05 3.843765e-05 7.005197e-05 0.0001016335 0.0001749579
## [8,] -1.368265e-04 -2.960422e-05 5.952995e-05 0.0001079052 0.0001654257
## [,6] [,7] [,8]
## [1,] 0.0001128708 1.992816e-05 -1.368265e-04
## [2,] 0.0001804591 3.843765e-05 -2.960422e-05
## [3,] 0.0001458528 7.005197e-05 5.952995e-05
## [4,] 0.0001334081 1.016335e-04 1.079052e-04
## [5,] 0.0002478819 1.749579e-04 1.654257e-04
## [6,] 0.0004263950 2.171438e-04 2.892748e-04
## [7,] 0.0002171438 4.886698e-04 3.805322e-04
## [8,] 0.0002892748 3.805322e-04 7.617394e-04
##
## $timeVec
## [1] 2004 2005 2006 2007 2009 2010 2011 2012
##
## $referencePeriod
## [1] 2008
##
## $prePeriodIndices
## [1] 1 2 3 4
##
## $postPeriodIndices
## [1] 5 6 7 8Nous pouvons, à partir de là, reconstituer le Granger plot. Celui-ci correspond aux coefficients et à leurs intervalles de confiance à 95% issus de l’estimation du modèle suivant :
outcomei,t=γi+γt+K=2012∑k≥2004;k≠2008βk.Traité.Tk+ϵi,t
où i correspond aux entreprises, t à l’année considéré et K à la position par rapport à la date de référence (ici 2008).
Mettons les éléments chargés en forme afin d’établir le graphe plus facilement.
dat_BC<-data.frame(
t=c(BCdata_EventStudy$timeVec,2008),
beta=c(BCdata_EventStudy$betahat,0),
sd=c(sqrt(diag(BCdata_EventStudy$sigma)),0)) %>%
arrange(t) %>%
mutate(dow=beta-1.96*sd,up=beta+1.96*sd)
dat_BC## t beta sd dow up
## 1 2004 0.006696352 0.02903163 -0.05020565 0.06359836
## 2 2005 0.029345034 0.02534841 -0.02033786 0.07902792
## 3 2006 -0.006472972 0.02286908 -0.05129638 0.03835043
## 4 2007 0.073014989 0.01757724 0.03856359 0.10746639
## 5 2008 0.000000000 0.00000000 0.00000000 0.00000000
## 6 2009 0.195961118 0.01897289 0.15877426 0.23314798
## 7 2010 0.312063903 0.02064933 0.27159121 0.35253660
## 8 2011 0.239541546 0.02210588 0.19621403 0.28286906
## 9 2012 0.126042500 0.02759963 0.07194723 0.18013777Ceci fait passons à l’assemblage du Granger plot. Ici, nous n’utiliserons pas ggcoef() de GGally mais simplement le classique geom_errorbar().
ggplot(data=dat_BC,aes(x=t,y=beta))+
geom_hline(yintercept = 0, linetype="dashed")+
geom_vline(xintercept = 2008,linetype="dashed")+
geom_errorbar(aes(ymin = dow,ymax=up),width=0.2,
linewidth=1)+
geom_point(color='red')+
labs(title="Effet dynamique du traitement - log(profit)",
subtitle = "intervalle de confiance à 95%")+
scale_x_continuous(breaks = 2004:2012)+
theme_minimal()+
theme(
plot.title = element_text(hjust=0.5),
plot.subtitle = element_text(hjust=0.5),
axis.title = element_blank()
)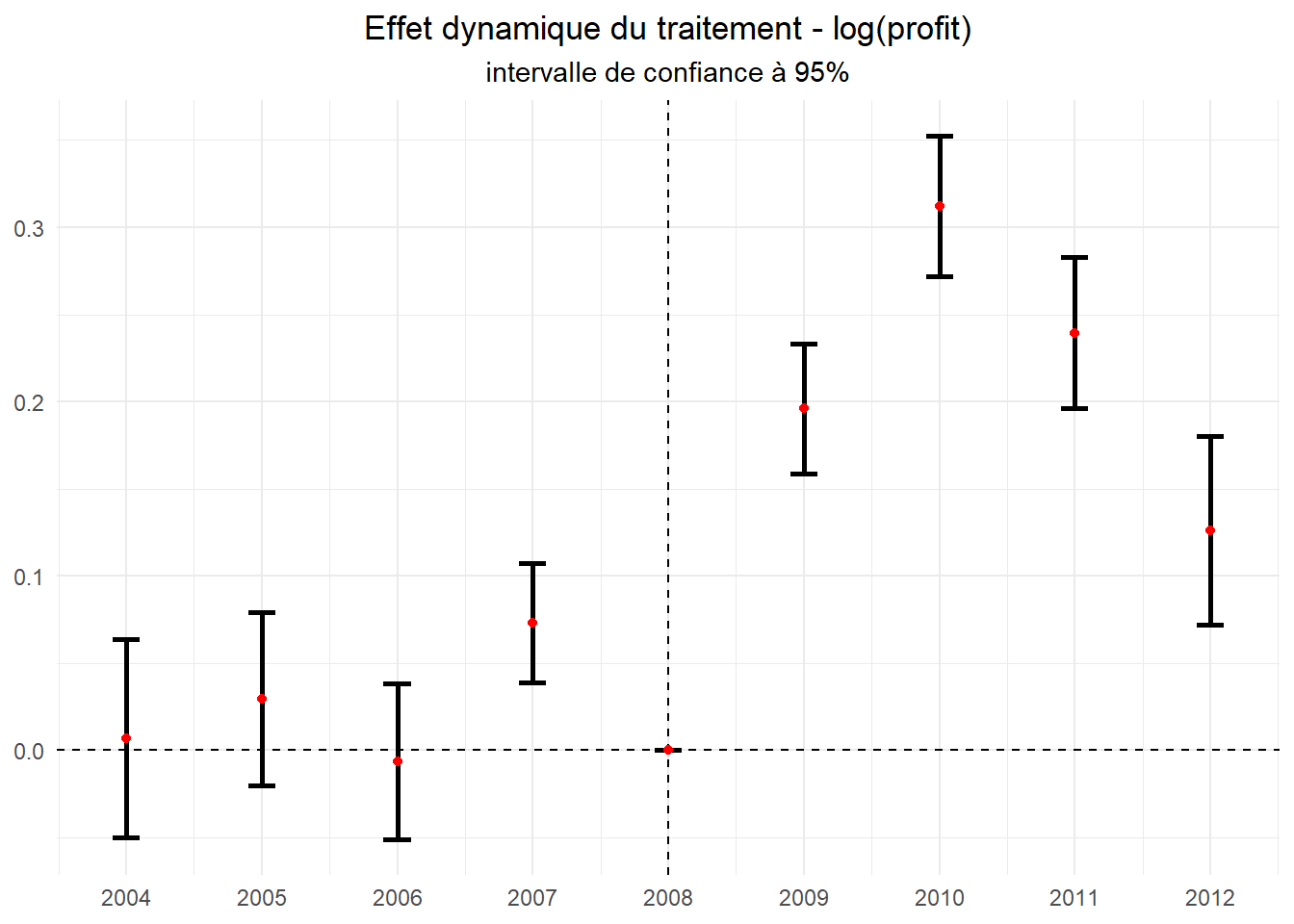
On voit clairement que l’hypothèse de coefficients tous égaux à zéro sur la période pré-traitement ne peut être retenue. L’intervalle de confiance produit pour 2007 ne comprend pas la valeur zéro. Cela conduit selon la logique des tests classiques à rejeter l’hypothèse de parallel trend et donc à remettre en cause le résultat de l’analyse diff-in-diff. La difficulté ici est qu’il puisse y avoir un choc macro-économique, ou simplement sectoriel, non observé (non pris en compte dans l’estimation) qui affecterait les restaurants de manière différente des autres entreprises de service même en l’absence de changement dans le taux de TVA. Cela rend l’identification de l’effet spécifique de ce changement impossible.
Néanmoins, si on observe bien les coefficients en post-traitement, on constate qu’ils sont bien plus grand que tous coefficients de la période pré-traitement (même celui de 2007). Il est ainsi tentant de continuer. C’est là que l’analyse de sensibilité proposée Rambachan et Roth par devient intéressante.
On postule que l’impact du choc n’est potentiellement pas suffisant pour expliquer l’augmentation des différences entre les groupes post-traitement. Aussi, si l’on prolonge la tendance issue des données pré-traitement, on pourrait constater la persistance d’un décalage allant dans le sens d’un effet spécifique au traitement. Néanmoins, il n’est pas nécessairement raisonnable d’imposer à l’effet du choc non contrôlé par la diff-in-diff une tendance lisse. La technique consiste alors établir l’effet du traitement pour différent niveau de violation de la parallel trend. Il s’agira alors d’identifier le niveau conduisant à rendre l’effet du traitement non significatif.
Le package HonestDiD permet de réaliser les calculs associés. La fonction createSensitivityResults_relativeMagnitudes() opère l’estimation d’une série d’intervalles de confiance robustes correspondant à différentes magnitudes de violation de la parallel trend. Ses arguments de base sont les effets moyens estimés (les bêta) pour les différentes périodes, la matrice variance-covariance associée, le type d’estimation à partiquer, les périodes pré et post traitement, la ou les périodes post traitement pour la ou lesquelles les estimations seront réalisées, les niveaux de distorsion examinés de manière iterative, ainsi que des paramètres du processus de simulation mis en oeuvre (généralement fixés pour limiter le temps de calcule).
Appliquons cela pour à l’effet de la baisse de TVA en 2009, l’année du traitement. Considérons des niveaux de distorsion croissant de 0,5 à 2 avec un pas de 0,5.
d_rm_r<- createSensitivityResults_relativeMagnitudes(
betahat = BCdata_EventStudy$betahat,
sigma = BCdata_EventStudy$sigma,
bound = "deviation from parallel trends",
numPrePeriods = 4,numPostPeriods = 4,
l_vec = c(1,0,0,0),Mbarvec = seq(0.5,2,0.5),
gridPoints = 100, grid.lb = -1, grid.ub = 1,
seed=1234)
d_rm_r## # A tibble: 4 × 5
## lb ub method Delta Mbar
## <dbl> <dbl> <chr> <chr> <dbl>
## 1 0.131 0.253 C-LF DeltaRM 0.5
## 2 0.0707 0.313 C-LF DeltaRM 1
## 3 0.0303 0.354 C-LF DeltaRM 1.5
## 4 -0.0303 0.414 C-LF DeltaRM 2Voyons comment ces résultats s’interprètent. Commençons par le plus simple, le cas où Mbar est fixé à 1. Cette valeur signifie que nous avons restreint le niveau de violations de la parallel trend sur la période post-traitement examinée à celle prévalant sur la période pré-traitement. Pour ce niveau de distorsion, l’effet du traitement (en 2009) peut être évalué entre 0,07 et 0,31 (à 95%). Il reste ainsi statistiquement significatif. Même si l’intervalle de confiance est plus large que celui produit sous l’hypothèse de parallel trend, celui-ci n’inclut pas la valeur 0.
C’est à partir de Mbar fixé à 2, autrement-dit d’un niveau de violation de la parallel trend appliquée sur la période post-traitement correspondant à deux fois celui prévalant sur la période pré-traitement, que l’effet du traitement devient statistiquement non significatif (avec un intervalle de confiance établie entre -0,03 et 0,41 et donc incluant zéro).
Ces différents éléments sont généralement mis en regard avec le issus du Granger plot pour la période ou les périodes réunies considérées dans un visuel. Le package HonestDiD propose une fonction permettant de réaliser l’opération, createSensitivityPlot_relativeMagnitudes(), que l’on peut employer avec la fonction contructOrigninalCS(), qui permet d’isoler les éléments de l’estimation de base nécessaire à la comparaison. Le graphe obtenu est au format ggplot ce qui permet des mises en forme facilitées.
O_R <- constructOriginalCS(betahat = BCdata_EventStudy$betahat,
sigma = BCdata_EventStudy$sigma,
numPrePeriods = 4,numPostPeriods = 4,
l_vec=c(1,0,0,0))
createSensitivityPlot_relativeMagnitudes(d_rm_r, O_R)+
geom_hline(yintercept = 0,color="white")+
geom_hline(yintercept = 0,linetype="dashed")+
labs(title = "Log Profits, 2009",
subtitle=latex2exp::TeX("$\\delta=\\delta^{RM}.(\\bar{M})$"))+
scale_x_continuous(breaks = seq(-0.5,2,0.5))+
theme_minimal()+
theme(
plot.title = element_text(hjust=0.5),
plot.subtitle = element_text(hjust=0.5),
legend.position = 'top',
legend.title = element_blank())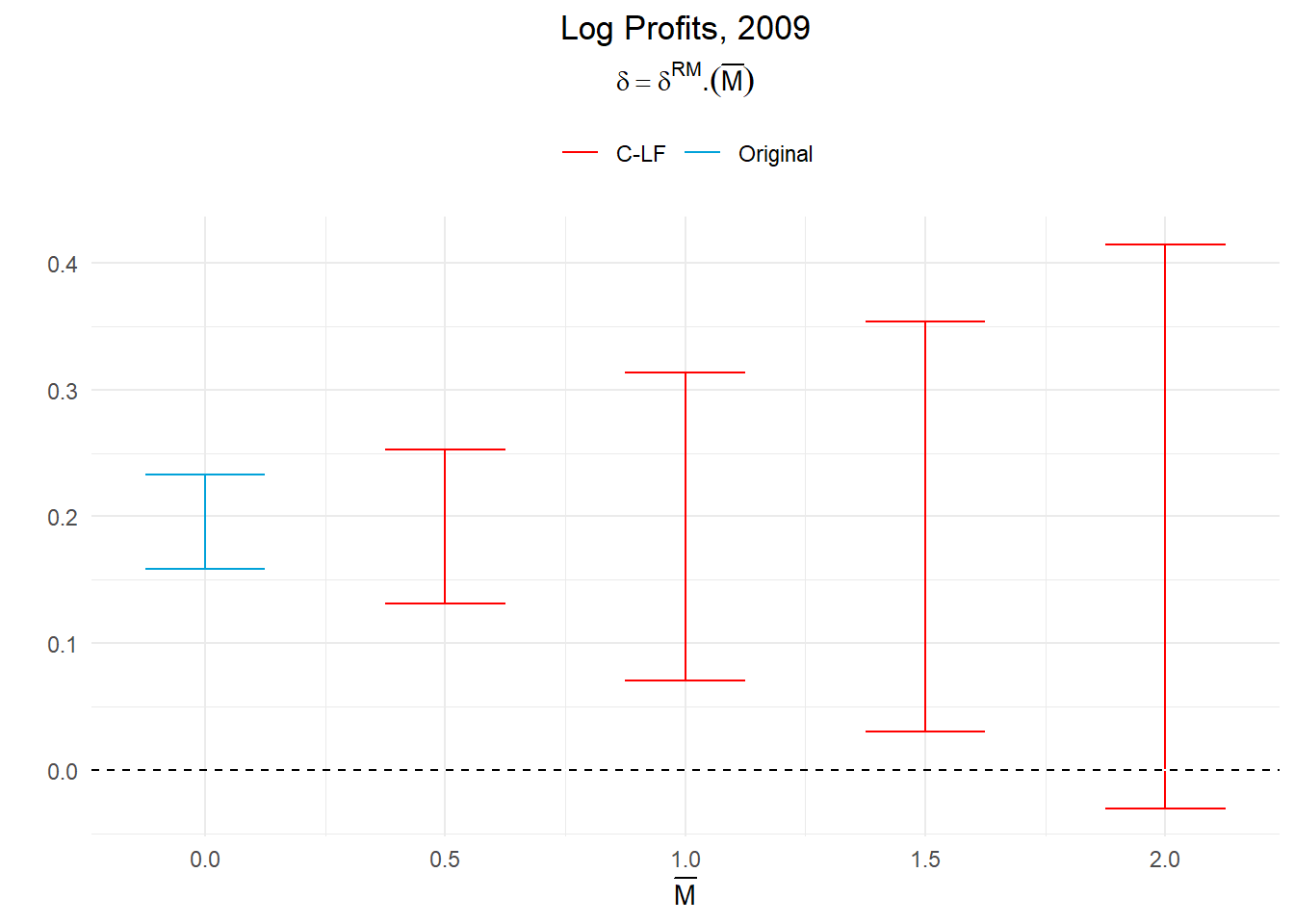
On voit bien que le résultat tiens jusqu’à la affectation d’une violation de la parallel trend sur la période post-traitement au regard de celle au maximum constatée sur la période pré-traitement (ˉM) de 2.
Pour conclure sur l’effet du traitement, il faut décider si une violation aussi importante est plausible. Dans la mesure où la France a connu une récession assez sévère en 2009, il est plausible que le facteur affectant de manière différente les restaurants par rapport aux autres entreprises de service soit plus important cette année là que sur la période pré-traitement (mais est-elle deux fois plus importante?).
Cette approche nous permet de formaliser les conditions de rejet de l’effet du traitement au regard du contexte.
Le même type d’analyse peut être réaliser pour l’effet causal moyen sur l’ensemble de la période post-traitement (pas juste une année mais les 4 disponibles). Dans ce cas, la procédure est la même, si ce n’est le vecteur de pondération lvect attribue un poids équivalent à chaque période post-traitement. On a ainsi:
d_rm_r_<- createSensitivityResults_relativeMagnitudes(
betahat = BCdata_EventStudy$betahat,
sigma = BCdata_EventStudy$sigma,
bound = "deviation from parallel trends",
numPrePeriods = 4,numPostPeriods = 4,
l_vec = c(0.25,0.25,0.25,0.25),Mbarvec = seq(0.5,2,0.5),
gridPoints = 100, grid.lb = -1, grid.ub = 1,
seed=1234)
d_rm_r_## # A tibble: 4 × 5
## lb ub method Delta Mbar
## <dbl> <dbl> <chr> <chr> <dbl>
## 1 0.0707 0.354 C-LF DeltaRM 0.5
## 2 -0.0505 0.495 C-LF DeltaRM 1
## 3 -0.192 0.636 C-LF DeltaRM 1.5
## 4 -0.333 0.778 C-LF DeltaRM 2La table ne montre que dés ˉM égal 1 l’intervalle de confiance comprend la valeur zéro. Le traitement n’a alors pas d’effet significatif.
Par ailleurs, on peut noter qu’il apparaît un peu plus de deux fois plus grand que celui que nous avions obtenu pour la seule année 2009. Cela est un effet mécanique associé à la multiplication des périodes post-traitement. Mais laissons cela de coté pour examiner la situation globale avec un graphe.
O_R_ <- constructOriginalCS(betahat = BCdata_EventStudy$betahat,
sigma = BCdata_EventStudy$sigma,
numPrePeriods = 4,numPostPeriods = 4,
l_vec=c(0.25,0.25,0.25,0.25))
createSensitivityPlot_relativeMagnitudes(d_rm_r_, O_R_)+
geom_hline(yintercept = 0,color="white")+
geom_hline(yintercept = 0,linetype="dashed")+
labs(title = "Log Profits, post",
subtitle=latex2exp::TeX("$\\delta=\\delta^{RM}.(\\bar{M})$"))+
scale_x_continuous(breaks = seq(-0.5,2,0.5))+
theme_minimal()+
theme(
plot.title = element_text(hjust=0.5),
plot.subtitle = element_text(hjust=0.5),
legend.position = 'top',
legend.title = element_blank())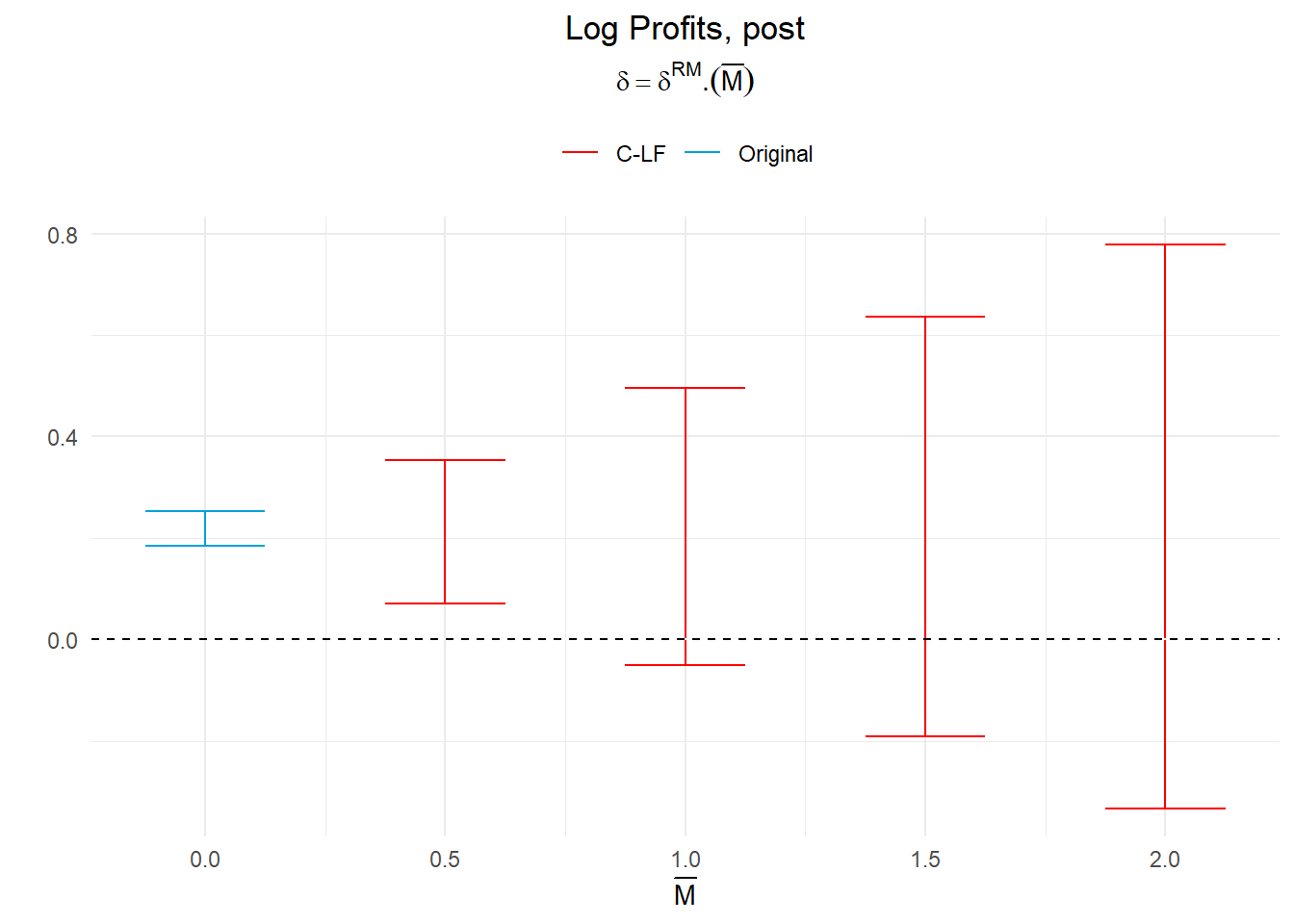
Restons en là. Jonathan Roth seul ou avec son coauteur Ashesh Rambachan propose d’aller au delà des tests classiques portant sur la parallel trend hypothesis, dont l’examen est un prérequi pour l’identification d’un effet causal via l’analyse diff-in-diff, soit en ayant du recul sur leur capacité à mettre en évidence une violation, soit en prolongeant l’analyse pour établir la taille de la violation potentielle qui conduirait à remettre en question les résultats de l’analyse diff-in-diff. Pour ce faire, ils proposent des outils que nous avons présenté ici rapidement. J’espère que cette bref introduction vous sera utile et vous aura convaincu de l’utilité de ces analyses complémentaires.