Pour cette troisième note “rapide” sur la méthode Difference-in-Difference, nous allons considérer deux exemples tirés du cours d’introduction aux méthodes causales proposé par A. Colin Cameron de l’université de Californie-Davis (que vous trouverez ici). Ils sont initialement développés à partir de Stata. Nous nous efforcerons à la fois de les reproduire sous R et d’approfondir différents concepts. Mais avant d’aller plus loin, comme à chaque fois, chargeons les packages que nous allons utiliser: le tidyverse, que l’on ne présente plus, et haven, qui permet de lire et écrire des fichiers notamment au format .dta (le format de Stata), labbeled, qui permet de travailler plus facilement les données à étiquette (comme celles issues de Stata), fixest, qui permet l’estimation de modèles à effets fixes, lmtest et sandwich, qui permettent de réaliser des tests spécifiques sur les coefficients de régression, et car, qui proposent des tests complémentaires.
# packages de gestion des données
library(tidyverse)
library(haven)
library(labelled)
# packages de regression et tests
library(fixest)
library(lmtest)
library(sandwich)
library(car)2x2 Difference in Difference
Ceci fait, abordons la première partie. L’ensemble est tiré de Tanaka (2014). Dans ce papier, l’auteur se pose la question de savoir si un meilleur accès aux soins améliore la santé. Plus précisément si la gratuité des soins à un impacte positif sur le statut nutritionnel des enfants pauvres. Pour ce faire, il prend la cas de l’Afrique du sud post-Apartheid. Cela lui permet d’exploiter une variation exogène de la tarification des services de santé, le passage à la gratuité. et des différences marquées concernant l’implantation des cliniques sur le territoire héritées du régime discriminatoire qui régnait dans le pays avant 1991. En 1994, le gouvernement rend gratuit les services de santé pour les enfants de moins de 6 ans. Il s’agira ici de la date de traitement. Le changement tarifaire augmente en principe l’accès aux soins. Néanmoins, pour que cela soit effectif, il faut que les ménages pauvres résident dans une région avec une clinique (aient un accès possible aux soins). Les enfants des ménages situés dans de telles régions sont le groupe traité. Les enfants des ménages est situés dans une région sans clinique, où la gratuité ne sert à rien puisque l’accès matériel aux soins reste très difficile, sont le groupe de contrôle.
Chargement et exploration des données
Chargeons les données de l’étude. Celles-ci sont disponibles ici. Le fichier est un .dta. Utilisons la fonction read correspondant dans le package haven.
dat<-read_dta("AED_HEALTHACCESS.dta")Voyons ce que l’on a. Commençons dénombrer les variables et les observations.
data.frame(nb_obs=nrow(dat),nb_var=length(dat))## nb_obs nb_var
## 1 1071 26La base obtenue comprend 1071 observations pour 26 variables, mais qu’elles sont-elles? Un des avantages des bases de données issues de logiciels comme Stata est qu’ils attachent différents attributs aux objets qu’ils traitent. Parmi eux, on trouve notamment des labels contenant de courts textes descriptifs des variables (ce qui peut être utile).
Pour obtenir, la liste des attributs d’un objet. Il suffit d’utiliser le fonction attributes(). Utilisons la sur dat notre base de données.
dat %>% attributes()## $class
## [1] "tbl_df" "tbl" "data.frame"
##
## $row.names
## [1] 1 2 3 4 5 6 7 8 9 10 11 12 13 14
## [15] 15 16 17 18 19 20 21 22 23 24 25 26 27 28
## [29] 29 30 31 32 33 34 35 36 37 38 39 40 41 42
## [43] 43 44 45 46 47 48 49 50 51 52 53 54 55 56
## [57] 57 58 59 60 61 62 63 64 65 66 67 68 69 70
## [71] 71 72 73 74 75 76 77 78 79 80 81 82 83 84
## [85] 85 86 87 88 89 90 91 92 93 94 95 96 97 98
## [99] 99 100 101 102 103 104 105 106 107 108 109 110 111 112
## [113] 113 114 115 116 117 118 119 120 121 122 123 124 125 126
## [127] 127 128 129 130 131 132 133 134 135 136 137 138 139 140
## [141] 141 142 143 144 145 146 147 148 149 150 151 152 153 154
## [155] 155 156 157 158 159 160 161 162 163 164 165 166 167 168
## [169] 169 170 171 172 173 174 175 176 177 178 179 180 181 182
## [183] 183 184 185 186 187 188 189 190 191 192 193 194 195 196
## [197] 197 198 199 200 201 202 203 204 205 206 207 208 209 210
## [211] 211 212 213 214 215 216 217 218 219 220 221 222 223 224
## [225] 225 226 227 228 229 230 231 232 233 234 235 236 237 238
## [239] 239 240 241 242 243 244 245 246 247 248 249 250 251 252
## [253] 253 254 255 256 257 258 259 260 261 262 263 264 265 266
## [267] 267 268 269 270 271 272 273 274 275 276 277 278 279 280
## [281] 281 282 283 284 285 286 287 288 289 290 291 292 293 294
## [295] 295 296 297 298 299 300 301 302 303 304 305 306 307 308
## [309] 309 310 311 312 313 314 315 316 317 318 319 320 321 322
## [323] 323 324 325 326 327 328 329 330 331 332 333 334 335 336
## [337] 337 338 339 340 341 342 343 344 345 346 347 348 349 350
## [351] 351 352 353 354 355 356 357 358 359 360 361 362 363 364
## [365] 365 366 367 368 369 370 371 372 373 374 375 376 377 378
## [379] 379 380 381 382 383 384 385 386 387 388 389 390 391 392
## [393] 393 394 395 396 397 398 399 400 401 402 403 404 405 406
## [407] 407 408 409 410 411 412 413 414 415 416 417 418 419 420
## [421] 421 422 423 424 425 426 427 428 429 430 431 432 433 434
## [435] 435 436 437 438 439 440 441 442 443 444 445 446 447 448
## [449] 449 450 451 452 453 454 455 456 457 458 459 460 461 462
## [463] 463 464 465 466 467 468 469 470 471 472 473 474 475 476
## [477] 477 478 479 480 481 482 483 484 485 486 487 488 489 490
## [491] 491 492 493 494 495 496 497 498 499 500 501 502 503 504
## [505] 505 506 507 508 509 510 511 512 513 514 515 516 517 518
## [519] 519 520 521 522 523 524 525 526 527 528 529 530 531 532
## [533] 533 534 535 536 537 538 539 540 541 542 543 544 545 546
## [547] 547 548 549 550 551 552 553 554 555 556 557 558 559 560
## [561] 561 562 563 564 565 566 567 568 569 570 571 572 573 574
## [575] 575 576 577 578 579 580 581 582 583 584 585 586 587 588
## [589] 589 590 591 592 593 594 595 596 597 598 599 600 601 602
## [603] 603 604 605 606 607 608 609 610 611 612 613 614 615 616
## [617] 617 618 619 620 621 622 623 624 625 626 627 628 629 630
## [631] 631 632 633 634 635 636 637 638 639 640 641 642 643 644
## [645] 645 646 647 648 649 650 651 652 653 654 655 656 657 658
## [659] 659 660 661 662 663 664 665 666 667 668 669 670 671 672
## [673] 673 674 675 676 677 678 679 680 681 682 683 684 685 686
## [687] 687 688 689 690 691 692 693 694 695 696 697 698 699 700
## [701] 701 702 703 704 705 706 707 708 709 710 711 712 713 714
## [715] 715 716 717 718 719 720 721 722 723 724 725 726 727 728
## [729] 729 730 731 732 733 734 735 736 737 738 739 740 741 742
## [743] 743 744 745 746 747 748 749 750 751 752 753 754 755 756
## [757] 757 758 759 760 761 762 763 764 765 766 767 768 769 770
## [771] 771 772 773 774 775 776 777 778 779 780 781 782 783 784
## [785] 785 786 787 788 789 790 791 792 793 794 795 796 797 798
## [799] 799 800 801 802 803 804 805 806 807 808 809 810 811 812
## [813] 813 814 815 816 817 818 819 820 821 822 823 824 825 826
## [827] 827 828 829 830 831 832 833 834 835 836 837 838 839 840
## [841] 841 842 843 844 845 846 847 848 849 850 851 852 853 854
## [855] 855 856 857 858 859 860 861 862 863 864 865 866 867 868
## [869] 869 870 871 872 873 874 875 876 877 878 879 880 881 882
## [883] 883 884 885 886 887 888 889 890 891 892 893 894 895 896
## [897] 897 898 899 900 901 902 903 904 905 906 907 908 909 910
## [911] 911 912 913 914 915 916 917 918 919 920 921 922 923 924
## [925] 925 926 927 928 929 930 931 932 933 934 935 936 937 938
## [939] 939 940 941 942 943 944 945 946 947 948 949 950 951 952
## [953] 953 954 955 956 957 958 959 960 961 962 963 964 965 966
## [967] 967 968 969 970 971 972 973 974 975 976 977 978 979 980
## [981] 981 982 983 984 985 986 987 988 989 990 991 992 993 994
## [995] 995 996 997 998 999 1000 1001 1002 1003 1004 1005 1006 1007 1008
## [1009] 1009 1010 1011 1012 1013 1014 1015 1016 1017 1018 1019 1020 1021 1022
## [1023] 1023 1024 1025 1026 1027 1028 1029 1030 1031 1032 1033 1034 1035 1036
## [1037] 1037 1038 1039 1040 1041 1042 1043 1044 1045 1046 1047 1048 1049 1050
## [1051] 1051 1052 1053 1054 1055 1056 1057 1058 1059 1060 1061 1062 1063 1064
## [1065] 1065 1066 1067 1068 1069 1070 1071
##
## $label
## [1] "Data for A. Colin Cameron (2022), ANALYSIS OF ECONOMIC DATA, Amazon"
##
## $notes
## [1] "Variable flag is constructed by CDC anthro program, values of 7 with all measures flagged were dropped from data set"
## [2] "-5 indicates individual not identified in 1998"
## [3] "Not all new cores chosen correctly but leave as is since likely to be key decision makers"
## [4] "Person codes for new and non-members (pcode >= 40) DO NOT represent the same person across split HHs"
## [5] "There are 38 split households, 3 of which are triples"
## [6] "February date indicate survey begun during pre-testing"
## [7] "Anthropometrist code incomplete, variable dropped"
## [8] "Some women 50 and over responded"
## [9] "Pregnancy history not always consistent with roster information"
## [10] "Instructions were altered so that adult parents were also measured"
## [11] "Children less than 6 months old not included"
## [12] "Calculations assume housing subsidy paid in kind"
## [13] "Must use number of facilities serving community and distance together"
## [14] "Despite instructions, a common mistake in this section is that when no facilities serving the community were identified, distance to nearest was not recorded (-4)"
## [15] "Old dates probably refer to when school first in area"
## [16] "No info for cluster 196 assumed same as neighboring 197"
## [17] "Clusters 80, 217 & 218 have little/no information on secondary schools"
## [18] "Cluster 210 missing from questionnaire"
## [19] "18"
##
## $names
## [1] "hhid93" "pcode" "idcommunity" "year" "hightreat"
## [6] "post" "postXhigh" "waz" "whz" "haz"
## [11] "fedu" "medu" "hhsizep" "lntotminc" "immuniz"
## [16] "nonclinic" "male" "age" "age93_0" "age93_1"
## [21] "age93_2" "age93_3" "age98_0" "age98_1" "age98_2"
## [26] "age98_3"On retrouve énormément d’éléments allant de la nature de l’objet aux noms des différentes variables qui le compose en passant par l’indexation des observations. Toutes ces informations ne sont pas nécessairement intéressantes… On peut les appeler une à une en les ciblant à l’aide de la fonction attr() en précisant l’élément via l’option which. Isolons le label de la base.
dat %>% attr(which='label')## [1] "Data for A. Colin Cameron (2022), ANALYSIS OF ECONOMIC DATA, Amazon"Ces commandes peuvent être utilisées sur chaque variable. Passons en revue les attributs de la variable waz.
attributes(dat$waz)## $label
## [1] "Weight for age z Score"
##
## $format.stata
## [1] "%6.2f"La commande peut être utilisée pour modifier l’attribut ou même en créer un. Traduisons le label de waz et ajoutons cette traduction à la variable comme attribut trad.
attributes(dat$waz)$trad<-"z Score pondéré par l'âge"
attributes(dat$waz)## $label
## [1] "Weight for age z Score"
##
## $format.stata
## [1] "%6.2f"
##
## $trad
## [1] "z Score pondéré par l'âge"Je ne saurais que vous conseiller de systématiquement ajouter ce type d’attributs à vos variables de manière à documenter votre travail particulièrement lorsque celui a vocation à être partagé.
On peut à partir de la fonction att() et de la commande d’itération sapply() répliquer la fonction describe de Stata.
data.frame(Type_stockage=sapply(dat,typeof),
Format=sapply(dat,attr,which='format.stata'),
Label=sapply(dat,attr,which='label'))## Type_stockage Format
## hhid93 double %10.0g
## pcode double %8.0g
## idcommunity double %10.0g
## year double %9.0g
## hightreat double %9.0g
## post double %9.0g
## postXhigh double %9.0g
## waz double %6.2f
## whz double %6.2f
## haz double %6.2f
## fedu double %9.0g
## medu double %9.0g
## hhsizep double %10.0g
## lntotminc double %9.0g
## immuniz double %8.0g
## nonclinic double %9.0g
## male double %9.0g
## age double %10.0g
## age93_0 double %9.0g
## age93_1 double %9.0g
## age93_2 double %9.0g
## age93_3 double %9.0g
## age98_0 double %9.0g
## age98_1 double %9.0g
## age98_2 double %9.0g
## age98_3 double %9.0g
## Label
## hhid93 Household identification No
## pcode 93: Person Code
## idcommunity Identifier for community
## year = 93 or 98
## hightreat = 1 if community has clinic in 1993
## post = 1 if year==98 and =0 if year==93
## postXhigh = post times hightreat
## waz Weight for age z Score
## whz Weight for height z Score
## haz Height for age z Score
## fedu Father's education
## medu Mother's education
## hhsizep Household size (all members)
## lntotminc Log of monthly household income
## immuniz Number of immunization campaigns since 1993
## nonclinic Number of health facilities other than clinic in 1993
## male = 1 if male
## age Precise age in fractions of year
## age93_0 =1 if age 0 in 1993
## age93_1 =1 if age 1 in 1993
## age93_2 =1 if age 2 in 1993
## age93_3 =1 if age 3 in 1993
## age98_0 =1 if age 0 in 1998
## age98_1 =1 if age 1 in 1998
## age98_2 =1 if age 2 in 1998
## age98_3 =1 if age 3 in 1998Le même type de résultat (en moins ergonomique) peut être obtenu via str().
dat %>% str()## tibble [1,071 × 26] (S3: tbl_df/tbl/data.frame)
## $ hhid93 : num [1:1071] 590020 590100 590100 590110 590070 ...
## ..- attr(*, "label")= chr "Household identification No"
## ..- attr(*, "format.stata")= chr "%10.0g"
## $ pcode : num [1:1071] 41 41 9 40 5 44 45 43 40 9 ...
## ..- attr(*, "label")= chr "93: Person Code"
## ..- attr(*, "format.stata")= chr "%8.0g"
## $ idcommunity: num [1:1071] 59 59 59 59 59 59 59 59 59 59 ...
## ..- attr(*, "label")= chr "Identifier for community"
## ..- attr(*, "format.stata")= chr "%10.0g"
## $ year : num [1:1071] 98 98 93 98 93 98 98 98 98 93 ...
## ..- attr(*, "label")= chr "= 93 or 98"
## ..- attr(*, "format.stata")= chr "%9.0g"
## $ hightreat : num [1:1071] 1 1 1 1 1 1 1 1 1 1 ...
## ..- attr(*, "label")= chr "= 1 if community has clinic in 1993"
## ..- attr(*, "format.stata")= chr "%9.0g"
## $ post : num [1:1071] 1 1 0 1 0 1 1 1 1 0 ...
## ..- attr(*, "label")= chr "= 1 if year==98 and =0 if year==93"
## ..- attr(*, "format.stata")= chr "%9.0g"
## $ postXhigh : num [1:1071] 1 1 0 1 0 1 1 1 1 0 ...
## ..- attr(*, "label")= chr "= post times hightreat"
## ..- attr(*, "format.stata")= chr "%9.0g"
## $ waz : num [1:1071] 0.73 0.64 -0.17 0.59 -0.62 ...
## ..- attr(*, "label")= chr "Weight for age z Score"
## ..- attr(*, "format.stata")= chr "%6.2f"
## ..- attr(*, "trad")= chr "z Score pondéré par l'âge"
## $ whz : num [1:1071] 1.18 2.72 -0.44 4.62 0.74 ...
## ..- attr(*, "label")= chr "Weight for height z Score"
## ..- attr(*, "format.stata")= chr "%6.2f"
## $ haz : num [1:1071] -0.22 -2.6 -0.04 -5.68 -2.06 ...
## ..- attr(*, "label")= chr "Height for age z Score"
## ..- attr(*, "format.stata")= chr "%6.2f"
## $ fedu : num [1:1071] 0 0 0 0 0 0 0 9 10 8 ...
## ..- attr(*, "label")= chr "Father's education"
## ..- attr(*, "format.stata")= chr "%9.0g"
## $ medu : num [1:1071] 7 0 10 7 6 10 8 0 0 6 ...
## ..- attr(*, "label")= chr "Mother's education"
## ..- attr(*, "format.stata")= chr "%9.0g"
## $ hhsizep : num [1:1071] 6 7 9 6 5 16 16 16 10 9 ...
## ..- attr(*, "label")= chr "Household size (all members)"
## ..- attr(*, "format.stata")= chr "%10.0g"
## $ lntotminc : num [1:1071] 8.56 7.7 7.94 7.71 4.94 ...
## ..- attr(*, "label")= chr "Log of monthly household income"
## ..- attr(*, "format.stata")= chr "%9.0g"
## $ immuniz : num [1:1071] 2 2 0 2 0 2 2 2 2 0 ...
## ..- attr(*, "label")= chr "Number of immunization campaigns since 1993"
## ..- attr(*, "format.stata")= chr "%8.0g"
## $ nonclinic : num [1:1071] 0 0 0 0 0 0 0 0 0 0 ...
## ..- attr(*, "label")= chr "Number of health facilities other than clinic in 1993"
## ..- attr(*, "format.stata")= chr "%9.0g"
## $ male : num [1:1071] 1 0 1 1 0 0 1 0 0 0 ...
## ..- attr(*, "label")= chr "= 1 if male"
## ..- attr(*, "format.stata")= chr "%9.0g"
## $ age : num [1:1071] 3.11 3.02 0 3.09 1.5 ...
## ..- attr(*, "label")= chr "Precise age in fractions of year"
## ..- attr(*, "format.stata")= chr "%10.0g"
## $ age93_0 : num [1:1071] 0 0 1 0 0 0 0 0 0 0 ...
## ..- attr(*, "label")= chr "=1 if age 0 in 1993"
## ..- attr(*, "format.stata")= chr "%9.0g"
## $ age93_1 : num [1:1071] 0 0 0 0 1 0 0 0 0 0 ...
## ..- attr(*, "label")= chr "=1 if age 1 in 1993"
## ..- attr(*, "format.stata")= chr "%9.0g"
## $ age93_2 : num [1:1071] 0 0 0 0 0 0 0 0 0 0 ...
## ..- attr(*, "label")= chr "=1 if age 2 in 1993"
## ..- attr(*, "format.stata")= chr "%9.0g"
## $ age93_3 : num [1:1071] 0 0 0 0 0 0 0 0 0 1 ...
## ..- attr(*, "label")= chr "=1 if age 3 in 1993"
## ..- attr(*, "format.stata")= chr "%9.0g"
## $ age98_0 : num [1:1071] 0 0 0 0 0 0 0 0 0 0 ...
## ..- attr(*, "label")= chr "=1 if age 0 in 1998"
## ..- attr(*, "format.stata")= chr "%9.0g"
## $ age98_1 : num [1:1071] 0 0 0 0 0 1 1 0 0 0 ...
## ..- attr(*, "label")= chr "=1 if age 1 in 1998"
## ..- attr(*, "format.stata")= chr "%9.0g"
## $ age98_2 : num [1:1071] 0 0 0 0 0 0 0 0 0 0 ...
## ..- attr(*, "label")= chr "=1 if age 2 in 1998"
## ..- attr(*, "format.stata")= chr "%9.0g"
## $ age98_3 : num [1:1071] 1 1 0 1 0 0 0 1 1 0 ...
## ..- attr(*, "label")= chr "=1 if age 3 in 1998"
## ..- attr(*, "format.stata")= chr "%9.0g"
## - attr(*, "label")= chr "Data for A. Colin Cameron (2022), ANALYSIS OF ECONOMIC DATA, Amazon"
## - attr(*, "notes")= chr [1:19] "Variable flag is constructed by CDC anthro program, values of 7 with all measures flagged were dropped from data set" "-5 indicates individual not identified in 1998" "Not all new cores chosen correctly but leave as is since likely to be key decision makers" "Person codes for new and non-members (pcode >= 40) DO NOT represent the same person across split HHs" ...Le package labelled a été créé spécifiquement pour travailler les bases dans lesquelles les variables présentes des attributs. Sa fonction look_for() permet d’obtenir un tableau proche de celui présenté par describe dans Stata. Je ne saurai que recommander son utilisation.
dat %>% look_for()## pos variable label col_type missing values
## 1 hhid93 Household identification No dbl 0
## 2 pcode 93: Person Code dbl 0
## 3 idcommunity Identifier for community dbl 0
## 4 year = 93 or 98 dbl 0
## 5 hightreat = 1 if community has clinic in 1993 dbl 0
## 6 post = 1 if year==98 and =0 if year==93 dbl 0
## 7 postXhigh = post times hightreat dbl 0
## 8 waz Weight for age z Score dbl 0
## 9 whz Weight for height z Score dbl 0
## 10 haz Height for age z Score dbl 0
## 11 fedu Father's education dbl 0
## 12 medu Mother's education dbl 0
## 13 hhsizep Household size (all members) dbl 0
## 14 lntotminc Log of monthly household income dbl 0
## 15 immuniz Number of immunization campaigns sinc~ dbl 0
## 16 nonclinic Number of health facilities other tha~ dbl 0
## 17 male = 1 if male dbl 0
## 18 age Precise age in fractions of year dbl 0
## 19 age93_0 =1 if age 0 in 1993 dbl 0
## 20 age93_1 =1 if age 1 in 1993 dbl 0
## 21 age93_2 =1 if age 2 in 1993 dbl 0
## 22 age93_3 =1 if age 3 in 1993 dbl 0
## 23 age98_0 =1 if age 0 in 1998 dbl 0
## 24 age98_1 =1 if age 1 in 1998 dbl 0
## 25 age98_2 =1 if age 2 in 1998 dbl 0
## 26 age98_3 =1 if age 3 in 1998 dbl 0Ceci étant posé. Continuons notre exploration de la base. Les différents relevés sont réalisés sur des zones administratives (community) qui sont ou non équipées en clinique. Si elles le sont, elle permet d’identifier le groupe des traités. Si elles ne le sont pas, elle permet d’identifier le groupe de contrôle. Dénombrons ces différents types de zone.
data.frame(nb_communauté=length(unique(dat$idcommunity)),
com_traitée=length(unique(dat$idcommunity[which(dat$hightreat==1)])),
com_controle=length(unique(dat$idcommunity[which(dat$hightreat==0)])))## nb_communauté com_traitée com_controle
## 1 54 26 28Les mesures sont faites sur 54 communautés dont 26 disposent de cliniques et 28 n’en disposent pas. Voyons ce qu’il en est des observations pour chaque communauté. Ce faisant, identifions les observations pré et post traitement (le passage à la gratuité en 94).
dat %>% group_by(idcommunity) %>%
summarise(nb_obs=n(),
statut=ifelse(sum(hightreat)==nb_obs,"traité","control"),
obs_pre=nb_obs-sum(post),
obs_post=sum(post))## # A tibble: 54 × 5
## idcommunity nb_obs statut obs_pre obs_post
## <dbl> <int> <chr> <dbl> <dbl>
## 1 59 12 traité 5 7
## 2 70 15 control 7 8
## 3 71 16 traité 10 6
## 4 74 3 control 2 1
## 5 77 1 traité 1 0
## 6 78 23 traité 14 9
## 7 79 20 control 10 10
## 8 80 32 traité 8 24
## 9 193 19 traité 13 6
## 10 195 10 traité 6 4
## # ℹ 44 more rowsOn remarque que le nombre d’observations est différent d’une communauté à l’autre et que ce nombre diffère également entre la période pré et la période post traitement. Nous n’avons donc pas ici un panel cylindré, autrement-dit des individus suivis sur l’ensemble de la durée de l’étude. Cela ne semble pas dû à une disparition des individus sur la période post traitement dans la mesure où pour certaine communauté le nombre d’observations est supérieure après le traitement.
Voyons ce qu’il en est globalement. Comptons le nombre d’observations du groupe des traités et du groupe de contrôle, toujours en distinguant les périodes avant et après traitement.
dat %>%
mutate(traite=ifelse(dat$hightreat==1,'traité','controle')) %>%
select(traite,post) %>%
group_by(traite) %>%
summarise(n=n(),av=n-sum(post),ap=sum(post),
ev=ap-av)## # A tibble: 2 × 5
## traite n av ap ev
## <chr> <int> <dbl> <dbl> <dbl>
## 1 controle 613 325 288 -37
## 2 traité 458 246 212 -34Il y a, quelque soit le groupe (traités ou contrôles), une diminution du nombre d’observations avec le temps.
On peut par ailleurs noter que les mesures avant/après ne sont prises qu’à deux dates: 1993, juste avant la réforme, et 1998, 4 ans après. Au delà de cette date la différence entre l’équipement en cliniques des communautés est devenue petite. L’équipement est alors bien plus homogène. Les différences ne permettraient surement plus d’établir du distinction nette.
dat %>%
mutate(traite=ifelse(dat$hightreat==1,'traité','controle')) %>%
select(traite,year) %>%
summarise(n=n(),.by=c(traite,year))## # A tibble: 4 × 3
## traite year n
## <chr> <dbl> <int>
## 1 traité 98 212
## 2 traité 93 246
## 3 controle 93 325
## 4 controle 98 288Pour avoir une vision encore plus claire de la structure de données, prenons le cas d’une communauté en particulier et examinons-la en détail. Prenons la numéro 59.
dat %>% filter(idcommunity==59)## # A tibble: 12 × 26
## hhid93 pcode idcommunity year hightreat post postXhigh waz whz
## <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl>
## 1 590020 41 59 98 1 1 1 0.73 1.18
## 2 590100 41 59 98 1 1 1 0.64 2.72
## 3 590100 9 59 93 1 0 0 -0.170 -0.440
## 4 590110 40 59 98 1 1 1 0.59 4.62
## 5 590070 5 59 93 1 0 0 -0.620 0.740
## 6 590090 44 59 98 1 1 1 3.48 6.02
## 7 590090 45 59 98 1 1 1 1.67 4.59
## 8 590090 43 59 98 1 1 1 1.08 0.93
## 9 590040 40 59 98 1 1 1 0.3 1.37
## 10 590010 9 59 93 1 0 0 2.5 2.13
## 11 590040 9 59 93 1 0 0 -0.460 0.130
## 12 590070 4 59 93 1 0 0 -1.54 -0.0600
## # ℹ 17 more variables: haz <dbl>, fedu <dbl>, medu <dbl>, hhsizep <dbl>,
## # lntotminc <dbl>, immuniz <dbl>, nonclinic <dbl>, male <dbl>, age <dbl>,
## # age93_0 <dbl>, age93_1 <dbl>, age93_2 <dbl>, age93_3 <dbl>, age98_0 <dbl>,
## # age98_1 <dbl>, age98_2 <dbl>, age98_3 <dbl>Plusieurs ménages ont plus d’une entrée dans l’extrait. Le ménage 590100 a deux entrées, le ménage 590090 en a trois. Jetons un oeil au premier.
dat %>% filter(idcommunity==59 & hhid93==590100)## # A tibble: 2 × 26
## hhid93 pcode idcommunity year hightreat post postXhigh waz whz haz
## <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl>
## 1 590100 41 59 98 1 1 1 0.64 2.72 -2.6
## 2 590100 9 59 93 1 0 0 -0.170 -0.440 -0.0400
## # ℹ 16 more variables: fedu <dbl>, medu <dbl>, hhsizep <dbl>, lntotminc <dbl>,
## # immuniz <dbl>, nonclinic <dbl>, male <dbl>, age <dbl>, age93_0 <dbl>,
## # age93_1 <dbl>, age93_2 <dbl>, age93_3 <dbl>, age98_0 <dbl>, age98_1 <dbl>,
## # age98_2 <dbl>, age98_3 <dbl>Les deux mesures sont réalisées sur l’échantillon des traités (hightreat égale à 1: là où il y a des cliniques en 1993). Il y en a une réalisée pré traitement et une post traitement. La mesure de 93 est faite sur une fille de moins d’un 1 an et la seconde en 98 sur un garçon de 3 ans.
On est loin d’avoir un panel. La spécification en two ways fixed effect (TWFE) n’est donc pas envisageable. nous resterons donc sur la spécification classique (2x2 Diff in Diff).
Maintenant que nous avons une vision plus claire de la structure de la base. Passons à l’analyse des variables. Revenons pour cela sur la définition de la variable expliquée waz. Il s’agit d’un Z-score autrement-dit le nombre d’écart-types qui sépare la valeur observée de la moyenne sur le groupe étudié. Ici, la mesure porte sur le poids des enfants. Le groupe étudié est défini par l’age de l’enfant. Ainsi, par exemple, une valeur de waz de -1 correspond à un enfant qui présenterait un poids inférieur de 1 écart-type à la moyenne des enfants de son âge. Plus cette mesure est négative, plus on est face à des enfants en mauvaise santé. Si le traitement, la gratuité des soins, est efficace après sa mise en oeuvre, on devrait constater une augmentation de la variable plus importante sur le groupe des traités que celle constatée sur le groupe de contrôle. Autrement-dit, on attend une Diff in Diff positive.
Pour commencer, limitons notre analyse à une Diff in Diff simple sans variables de contrôles. Ne gardons que waz, hightreat, post, postXhigh et idcommunity.
dat_red_1<- dat %>% select(waz,hightreat,post,postXhigh,idcommunity)Présentons quelques statistiques descriptives sur le modèle ce que propose Stata par défaut avec sa fonction summarize.
dat_red_1 %>%
select(-idcommunity) %>%
summarize_all(
.fun=list(~length(.),~mean(.),~sd(.),~min(.),~max(.))) %>%
unlist %>% matrix(nrow = 4, ncol=5) %>% as.data.frame() %>%
cbind(Variables=names(dat_red_1)[1:4],.) %>%
rename(Obs=V1,Mean=V2,Std.dev.=V3,Min=V4,Max=V5)## Variables Obs Mean Std.dev. Min Max
## 1 waz 1071 -0.2058730 1.5874317 -5.88 4.94
## 2 hightreat 1071 0.4276377 0.4949671 0.00 1.00
## 3 post 1071 0.4668534 0.4991332 0.00 1.00
## 4 postXhigh 1071 0.1979458 0.3986373 0.00 1.00waz est la seule variable continue du lot. On peut noter qu’elle est en moyenne négative. Les enfants objets de l’étude sont les enfants de famille pauvres. Ils présentent pour leur age un poids inférieur à la moyenne (des enfants du même age dans la population générale). Les autres variables sont catégorielles binaires. Leur moyenne correspond à des proportions. On a ainsi 42,7% des observations qui sont faîtes sur le groupe traité, 46,6% qui sont réalisées après 1994 (en 1998) et 19,7% des observations qui sont faîtes sur les traités après 94.
Analyses 2x2 Diff in Diff
Passons donc à l’analyse. Commençons par établir la matrice 2x2 des moyennes (contrôle/traité, avant/après).
moy_av_t<-dat_red_1 %>% filter(post==0&hightreat==0) %>%
summarise(av_t=mean(waz))
moy_ap_t<-dat_red_1 %>% filter(post==1&hightreat==0) %>%
summarise(ap_t=mean(waz))
moy_av_nt<-dat_red_1 %>% filter(post==0&hightreat==1) %>%
summarise(av_nt=mean(waz))
moy_ap_nt<-dat_red_1 %>% filter(post==1&hightreat==1) %>%
summarise(ap_nt=mean(waz))
mat<-c(moy_av_t,moy_ap_t,moy_av_nt,moy_ap_nt) %>% unlist() %>%
matrix(ncol=2,nrow=2,byrow=FALSE)
rownames(mat)<-c("avant","apres")
colnames(mat)<-c("control","traite")
rm(moy_av_t,moy_ap_t,moy_av_nt,moy_ap_nt)
mat## control traite
## avant -0.41418462 -0.5452439
## apres -0.06909722 0.3214623A partir de là, il est facile de calculer notre Diff in Diff. Il suffit de soustraire à l’évolution avant/après mesurée sur les traités l’évolution avant/après mesurée sur le groupe de contrôle.
(mat[2,2]-mat[1,2])-(mat[2,1]-mat[1,1])## [1] 0.5216188rm(mat)On a une augmentation moyenne de 0,52 points supérieurs de waz pour le groupe des traités (ceux qui avez une cliniques dans la communauté en 1993) par rapport au groupe de contrôle.
Le même résultat peut être obtenu à partir de la syntaxe dplyr.
moy<-dat_red_1 %>%
group_by(hightreat,post) %>%
summarise(moyenne=mean(waz),.groups='keep')
moy## # A tibble: 4 × 3
## # Groups: hightreat, post [4]
## hightreat post moyenne
## <dbl> <dbl> <dbl>
## 1 0 0 -0.414
## 2 0 1 -0.0691
## 3 1 0 -0.545
## 4 1 1 0.321moy<-moy%>%
pull(moyenne)
(moy[4]-moy[2])-(moy[3]-moy[1])## [1] 0.5216188Le passage à la gratuité semble bien permettre d’améliorer la santé des enfants pauvres pour qui les barrières non tarifaires ne sont pas un problème (ceux ayant accès à une clinique). Mais pour conclure, il nous faut un test statistique sur cette Diff in Diff. Pour l’obtenir, procédons à la régression habituelle. Concernant les tests sur les coefficients, nous optons pour un clustering sur la communauté. On postule donc qu’il y a plus de variance entre communautés qu’à l’intérieure des communautés.
reg<-lm(waz~hightreat+post+postXhigh,data=dat_red_1)
coeftest(reg,vcov. = vcovCL(reg,cluster=dat_red_1$idcommunity))##
## t test of coefficients:
##
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) -0.41418 0.11514 -3.5972 0.0003365 ***
## hightreat -0.13106 0.19681 -0.6659 0.5056042
## post 0.34509 0.13710 2.5170 0.0119810 *
## postXhigh 0.52162 0.23530 2.2168 0.0268447 *
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1Le test confirme bien le résultat.
On peut reconstituer la matrice des moyennes à partir des différents coefficients de la régression DID.
La constante correspond au waz moyen sur le groupe de contrôle avant la date du traitement (traite==0 , post==0 et donc traite::post==0). Pour obtenir, la moyenne sur le groupe de contrôle après la date du traitement (traite==0 , post==1 et donc traite::post==0), on additionne simplement la constante et le coefficient associé à post. Pour le groupe des traités avant le traitement (traite==1, post==0 et donc traite::post==0), on additionne simplement la constante et le coefficient associé à traite. Pour les traités post traitement (traite==1, post==1 et donc traite::post==1), il suffit de tout additionner constante compris.
cont_av<-coef(reg)[1] %>% sum()
cont_ap<-coef(reg)[c(1,3)] %>% sum()
trait_av<-coef(reg)[c(1,2)] %>% sum()
trait_ap<-coef(reg) %>% sum()
mat<-matrix(c(cont_av,cont_ap,trait_av,trait_ap),ncol=2)
colnames(mat)<-c('Controle','Traite')
rownames(mat)<-c('avant','aprés')
mat## Controle Traite
## avant -0.41418462 -0.5452439
## aprés -0.06909722 0.3214623La Diff in Diff évaluée est en quelque sorte brute (simple) dans la mesure où il n’y a pas de variables de contrôle. On peut sans difficulté en ajouter (mais cela peut poser un problème de bad controls dans certaines circonstances dont nous discuterons dans un prochain post). Faisons-le introduisons un effet fixe communauté, l’éducation de parent (homme et femme), la taille du ménage, le revue, le nombre de campagne de vaccinations sur la période, le nombre de clinique dans la communauté et si l’enfant est un garçon ou une fille. Sortons uniquement le coefficient donnant la Diff in Diff.
reg_<-lm(waz~hightreat+post+postXhigh+
factor(idcommunity)+fedu+medu+hhsizep+lntotminc+immuniz+nonclinic,
data=dat)
coeftest(reg_)[4,]## Estimate Std. Error t value Pr(>|t|)
## 0.642880667 0.212103613 3.030974622 0.002499841Ici, il n’est pas possible de reconstituer la matrice des moyennes dans la mesure où la constante est ajustée en fonction de l’ensemble des variables catégorielles de la régression (notamment ici les effets fixes communauté et le sexe de l’enfant…).
Ici, il est impossible de procéder à un quelconque test de parallel trend ou même un test placebo faute de granularité dans les données. Nous terminerons donc ce premier exemple avec un graphe. Pour cela, préparons les données mobilisées.
bas_g<-data.frame(traite=c("Controle","Controle","Traite","Traite"),
post=c("1993","1998","1993","1998"),
waz=c(mat[1,1],mat[2,1],
mat[1,2],mat[2,2]))
did<-coef(reg_)[4]
bas_g## traite post waz
## 1 Controle 1993 -0.41418462
## 2 Controle 1998 -0.06909722
## 3 Traite 1993 -0.54524390
## 4 Traite 1998 0.32146226Puis, établissons notre graphe.
ggplot(bas_g, aes(x = post,
y = waz,
color = traite)) +
geom_point() +
geom_line(aes(group = traite)) +
labs(title="Effet du passage à la gratuité sur la santé des enfants pauvres",
y="Z-score du poids moyen pondéré par classes d'âge",
color="")+
annotate(geom = "segment", x = "1993",
xend = "1998",
y = bas_g$waz[3],
yend = bas_g$waz[4] - did,
linetype = "dashed", color = "grey50") +
annotate(geom = "segment", x = "1998",
xend = "1998",
y = bas_g$waz[4] ,
yend = bas_g$waz[4] - did,
linetype = "dotted", color = "blue") +
annotate(geom = "label", x = "1998",
y = bas_g$waz[4] - (did / 2),
label = "effet du programme", size = 3)+
theme_bw()+
theme(
plot.title = element_text(hjust=0.5),
axis.title.x = element_blank(),
legend.position = "top"
)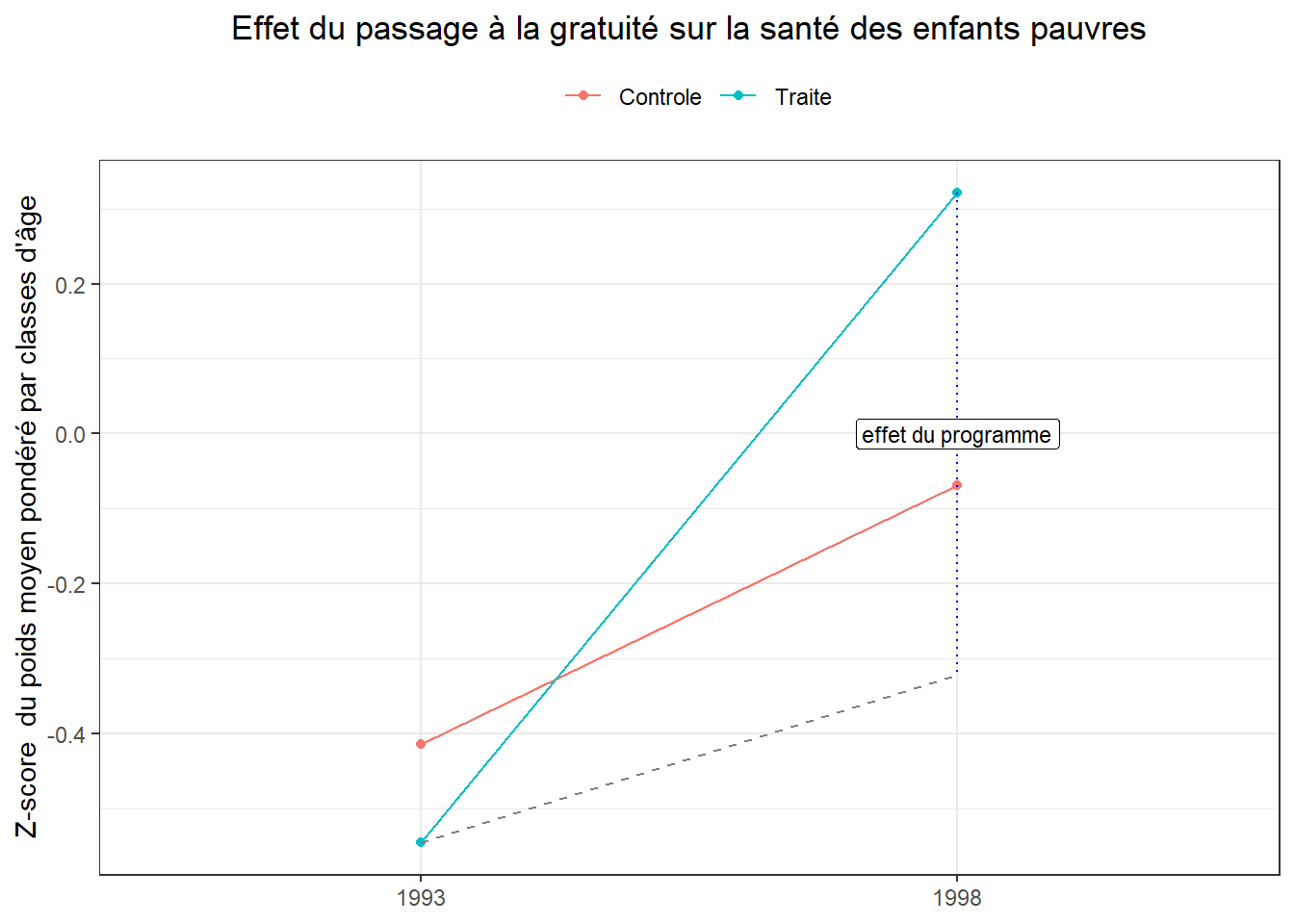
rm(list = ls(all.names = TRUE))Notez qu’ici la ligne pointillé n’est pas parallèle à la rouge comme ce devrait être le cas dans une Diff in Diff classique. Cela est dû à l’ajustement via les variables de contrôle.
Difference in Difference avec périodes multiples
Pour le second exemple développé, nous changeons de configuration avec cette fois plus de deux périodes de mesures (avant et après le traitement) et pour cela nous utiliserons une des bases de données mobilisées dans le manuel de Stata pour illustrer l’usage de sa fonction didregress. Dans cet application, on a un fournisseur de soins de santé qui gère des hôpitaux qui s’interroge sur l’impact de l’automatisation des procédures d’admission sur la satisfaction des patients. On a des données mensuelles sur les patients entre janvier et juillet. La procédure a été mise en place en avril dans une partie de ces hôpitaux.
Chargement et exploration des données
Les données sont à charger à partir de l’url associée au manuel de Stata 17. Pour cela, il suffit d’introduire l’adresse comme argument dans la fonction read_dta().
dat2<-read_dta("https://www.stata-press.com/data/r17/hospdd.dta")Ceci étant fait, voyons ce que contient la base. Comptons le nombre d’observations et le nombre de variables.
data.frame(nb_obs=nrow(dat2),nb_var=length(dat2))## nb_obs nb_var
## 1 7368 5On a 7 368 observations et 5 variables. Mais que représentent ces variables? Utilisons notre réplication de describe pour accéder aux labels des variables.
data.frame(Type_stockage=sapply(dat2,typeof),
Format=sapply(dat2,attr,which='format.stata'),
Label=sapply(dat2,attr,which='label'))## Type_stockage Format Label
## hospital double %9.0g Hospital ID
## frequency double %9.0g Hospital visit frequency
## month double %8.0g Month
## procedure double %9.0g Admission procedure
## satis double %9.0g Patient satisfaction scoreLes commentaires laissés ne sont pas très parlant. Revenons aux commandes R classiques avec str().
str(dat2)## tibble [7,368 × 5] (S3: tbl_df/tbl/data.frame)
## $ hospital : num [1:7368] 1 1 1 1 1 1 1 1 1 1 ...
## ..- attr(*, "label")= chr "Hospital ID"
## ..- attr(*, "format.stata")= chr "%9.0g"
## $ frequency: dbl+lbl [1:7368] 3, 2, 4, 2, 1, 1, 2, 4, 2, 2, 4, 1, 2, 3, 4, 2, 1, 2,...
## ..@ label : chr "Hospital visit frequency"
## ..@ format.stata: chr "%9.0g"
## ..@ labels : Named num [1:4] 1 2 3 4
## .. ..- attr(*, "names")= chr [1:4] "Low" "Medium" "High" "Very high"
## $ month : dbl+lbl [1:7368] 7, 3, 2, 4, 3, 7, 4, 1, 3, 1, 1, 4, 6, 1, 1, 4, 1, 2,...
## ..@ label : chr "Month"
## ..@ format.stata: chr "%8.0g"
## ..@ labels : Named num [1:7] 1 2 3 4 5 6 7
## .. ..- attr(*, "names")= chr [1:7] "January" "February" "March" "April" ...
## $ procedure: dbl+lbl [1:7368] 1, 0, 0, 1, 0, 1, 1, 0, 0, 0, 0, 1, 1, 0, 0, 1, 0, 0,...
## ..@ label : chr "Admission procedure"
## ..@ format.stata: chr "%9.0g"
## ..@ labels : Named num [1:2] 0 1
## .. ..- attr(*, "names")= chr [1:2] "Old" "New"
## $ satis : num [1:7368] 4.11 3.32 3.41 3 3.11 ...
## ..- attr(*, "label")= chr "Patient satisfaction score"
## ..- attr(*, "format.stata")= chr "%9.0g"
## - attr(*, "label")= chr "Artificial hospital admission procedure data"Les choses sont plus claires. hospital est l’identifiant des hôptiaux. frequency est un indicateur de la fréquentation des hôpitaux par le patient avec 5 valeurs (1 Low … 5 Very hight). month est le mois de la visite. Il va de 1 pour janvier à 7 pour juillet. procedure, qui est notre variable d’intérêt, prend la valeur 1 à la fois s’il l’hôpital est traité (s’il a automatisé sa procédure d’admission à partir d’avril) et si l’observation est effectuée en avril ou après (après la mise en place du traitement). satis est notre variable expliquée. Il s’agit d’une moyenne de différentes notes qui vont de 0 (pas satisfait du tout) à 10 (très très satisfait) attribuées par les patients sur quatre critères concernant l’admission.
look_for() permet d’obtenir quelque chose d’un peu mieux.
dat2 %>% look_for()## pos variable label col_type missing values
## 1 hospital Hospital ID dbl 0
## 2 frequency Hospital visit frequency dbl+lbl 0 [1] Low
## [2] Medium
## [3] High
## [4] Very high
## 3 month Month dbl+lbl 0 [1] January
## [2] February
## [3] March
## [4] April
## [5] May
## [6] June
## [7] July
## 4 procedure Admission procedure dbl+lbl 0 [0] Old
## [1] New
## 5 satis Patient satisfaction score dbl 0Voyons ce que donne ces variables. Regardons les premières observations.
dat2 %>% head()## # A tibble: 6 × 5
## hospital frequency month procedure satis
## <dbl> <dbl+lbl> <dbl+lbl> <dbl+lbl> <dbl>
## 1 1 3 [High] 7 [July] 1 [New] 4.11
## 2 1 2 [Medium] 3 [March] 0 [Old] 3.32
## 3 1 4 [Very high] 2 [February] 0 [Old] 3.41
## 4 1 2 [Medium] 4 [April] 1 [New] 3.00
## 5 1 1 [Low] 3 [March] 0 [Old] 3.11
## 6 1 1 [Low] 7 [July] 1 [New] 2.88On peut noter que l’on a pour un même hôpital et un même mois plusieurs observations. Simplement il y a plusieurs patients admis par mois. Rein d’étonnant. Mais examinons cela de plus prés. Combien y a t-il d’hôpitaux ?
length(unique(dat2$hospital))## [1] 46On a 46 hôpitaux. Combien y a-t-il d’observations par hôpital?
dat2 %>% count(hospital) %>% summarise(moy=mean(n))## # A tibble: 1 × 1
## moy
## <dbl>
## 1 160.On a en moyenne 160 observations par hôpital. Combien y a t-il d’observations par mois pour chaque hôpital?
dat2 %>% group_by(hospital,month) %>% count() ## # A tibble: 322 × 3
## # Groups: hospital, month [322]
## hospital month n
## <dbl> <dbl+lbl> <int>
## 1 1 1 [January] 46
## 2 1 2 [February] 23
## 3 1 3 [March] 23
## 4 1 4 [April] 23
## 5 1 5 [May] 23
## 6 1 6 [June] 23
## 7 1 7 [July] 23
## 8 2 1 [January] 42
## 9 2 2 [February] 21
## 10 2 3 [March] 21
## # ℹ 312 more rowsOn peut noter qu’il y a toujours plus d’observations sur le mois de janvier (1) que sur les autres et cela sur tous les hôpitaux.
Ok, disons que l’on a une vision générale de la structure des données. Intéressons-nous à la répartition du traitement. Voyons combien on a d’hôpitaux traités et combien constituent le groupe de contrôle.
cont<-dat2 %>%
group_by(hospital) %>%
summarise(b=ifelse(sum(procedure)==0,"Controles","Traités"))
table(cont$b)##
## Controles Traités
## 28 18rm(cont)Ce dénombrement apparaît dans la première partie de la sortie proposée par la fonction didregress de Stata. La seconde partie donne une information sur la première fois où on observe les groupes dans la base (comme non traité et comme traité). Répliquons-la.
ent<-dat2 %>%
group_by(hospital) %>%
mutate(b=ifelse(sum(procedure)==0,"Controles","Traités"),
m=month) %>%
group_by(hospital,b,procedure) %>%
summarise(min_=min(month), .groups = 'keep')
cbind(Controle=
c(minimum=min(ent$min_[which(ent$procedure==0&ent$b=="Controles")]),
maximum=max(ent$min_[which(ent$procedure==0&ent$b=="Controles")])),
Traite=
c(minimum=min(ent$min_[which(ent$procedure==1&ent$b=="Traités")]),
maximum=max(ent$min_[which(ent$procedure==1&ent$b=="Traités")])))## Controle Traite
## minimum 1 4
## maximum 1 4Ici, on a une base homogène. Toutes les observations du groupe de contrôle entrent dans la base dés le mois de janvier et le traitement est appliqué pour tous les traités en avril. On est sur une Diff in Diff classique pas une staggered.
Avant de la mettre en oeuvre, jetons un œil sur la distribution de la variable expliquée. Utilisons pour cela un histogramme rapidement fait.
ggplot(data=dat2,aes(x=satis))+
geom_histogram(color='black',bins=30)+
geom_vline(xintercept = mean(dat2$satis),color='red')+
theme_minimal()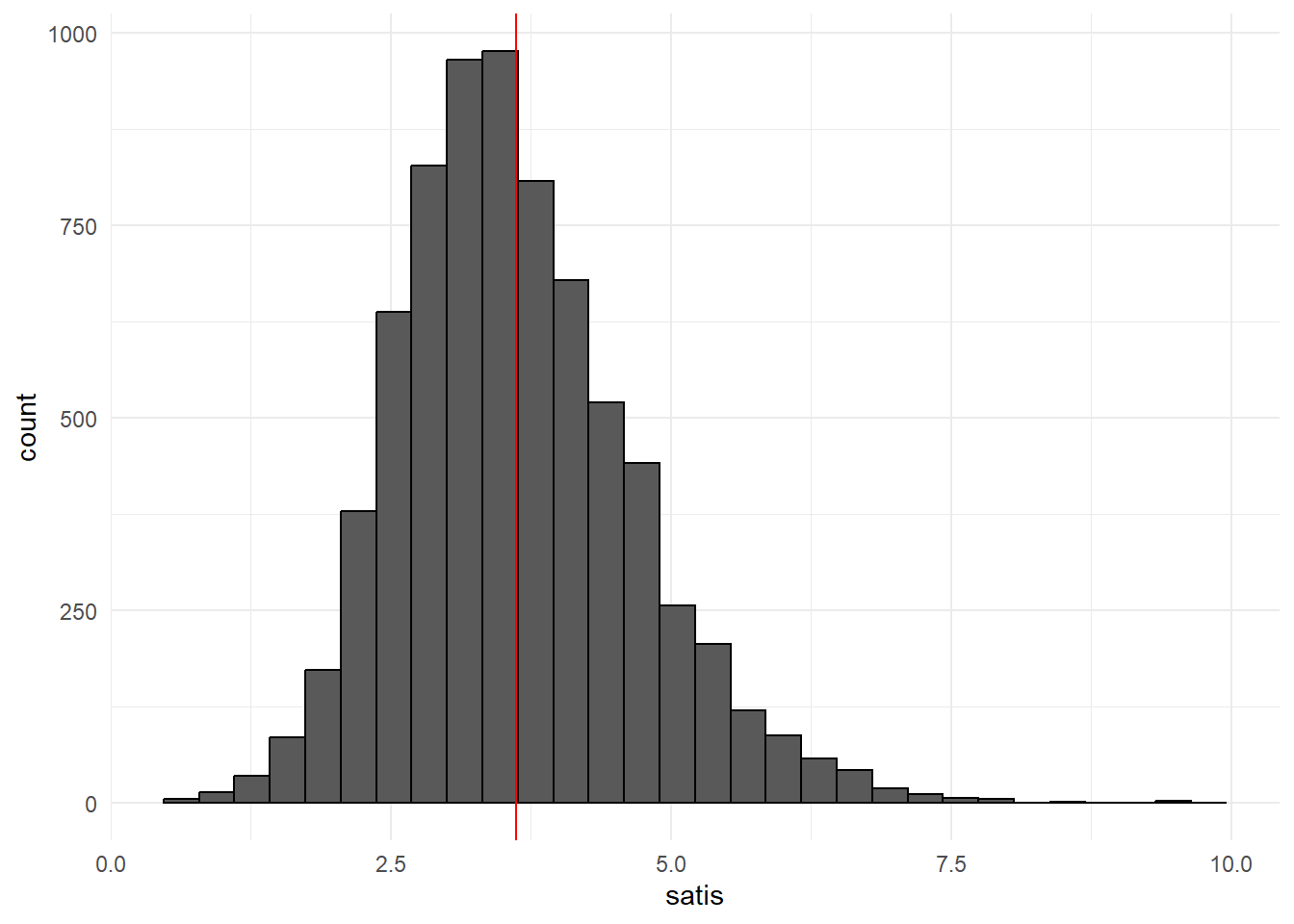
Elle présente une forme très proche de celle d’une loi normale.
Analyse Diff in Diff multipériodes
Maintenant que nous connaissons mieux la structure de nos données, on a des cross-sections répétées (pas un panel), nous pouvons procéder à l’estimation de notre Diff in Diff. Pour cela, nous utiliserons les TWFE (two ways fixed effects). Pour les tests sur le coefficient d’intérêt, dans la mesure où le recueil des données se fait par hôpitaux (et donc qu’il doit y avoir plus de variabilité entre les différents hôpitaux que sur les observations par hôpitaux), on utilise des erreurs standards clusterisées sur la base des hôpitaux. Le modèle estimé est le suivant:
\[ satis_{i,t,s}=\gamma_i+\gamma_t+D_{s,t}+\epsilon_{i,t,s} \]
où i correspond à un hôpital, t à un mois et s un individu. D indique si l’individu a été traité à la date t (ici s’il est passé par un hôpital qui avait mis en place la nouvelle procédure le mois où il a été soigné…).
On a ainsi:
reg_2<-lm(satis~procedure+factor(hospital)+factor(month),
data=dat2)
coeftest(reg_2,vcov.=vcovCL(reg_2,cluster=dat2$hospital))[2,] %>%
round(digits = 7)## Estimate Std. Error t value Pr(>|t|)
## 0.8479879 0.0321121 26.4071077 0.0000000Le test confirme l’effet positif de l’automatisation de la procédure d’admission. Cette automatisation permet en moyenne d’augmenter la note de satisfaction en moyenne de 0,85 points. Autrement-dit, si les hôpitaux traités (automatisés) ne l’avez pas été, la satisfaction aurait été 0,85 points plus bas.
Le même résultat peut être obtenu à partir d’une spécification classique en 2x2 Diff in Diff. Pour cela, il est nécessaire de commencer par réaliser quelque manipulations de données. Générons les variables Traite et post.
dat2_<-dat2 %>%
group_by(hospital) %>%
mutate(Traite=ifelse(sum(procedure)==0,"Controles","Traités"),
post=month>=4)Maintenant que l’on a les données pro format, procédons à la régression et sortons uniquement la ligne associée au coefficient Diff in Diff.
reg_<-lm(satis~Traite+post+Traite*post,data=dat2_)
coeftest(reg_,vcov.=vcovCL(reg_,cluster=dat2$hospital))[4,] %>%
round(digits = 7)## Estimate Std. Error t value Pr(>|t|)
## 0.8479879 0.0320051 26.4954049 0.0000000La spécification en TWFE ne permet pas de reconstituer la matrice des moyennes contrairement à celle en 2x2 Diff in Diff que nous venons de mettre en oeuvre. Établissons-la à partir de ses coefficients.
cont_av<-coef(reg_)[1] %>% sum()
cont_ap<-coef(reg_)[c(1,3)] %>% sum()
trait_av<-coef(reg_)[c(1,2)] %>% sum()
trait_ap<-coef(reg_) %>% sum()
mat<-matrix(c(cont_av,cont_ap,trait_av,trait_ap),ncol=2)
colnames(mat)<-c('Controle','Traite')
rownames(mat)<-c('avant','aprés')
rm(cont_av,cont_ap,trait_av,trait_ap)
mat## Controle Traite
## avant 3.392509 3.525383
## aprés 3.382490 4.363351Vérifions que l’ensemble est juste en recalculons notre double différence.
(mat[2,2]-mat[1,2])-(mat[2,1]-mat[1,1])## [1] 0.8479879Présentons notre résultat sur la forme d’un graphe. Pour cela, passons notre matrice de moyen en data frame et donnons lui une forme adéquate.
bas_g<-data.frame(traite=c("Controle","Controle","Traite","Traite"),
post=c("avant avril","avril et aprés avril",
"avant avril","avril et aprés avril"),
satis=c(mat[1,1],mat[2,1],
mat[1,2],mat[2,2]))
did<-coef(reg_)[4]
rm(mat)
bas_g## traite post satis
## 1 Controle avant avril 3.392509
## 2 Controle avril et aprés avril 3.382490
## 3 Traite avant avril 3.525383
## 4 Traite avril et aprés avril 4.363351Maintenant que nous avons notre data frame, réalisons le graphe.
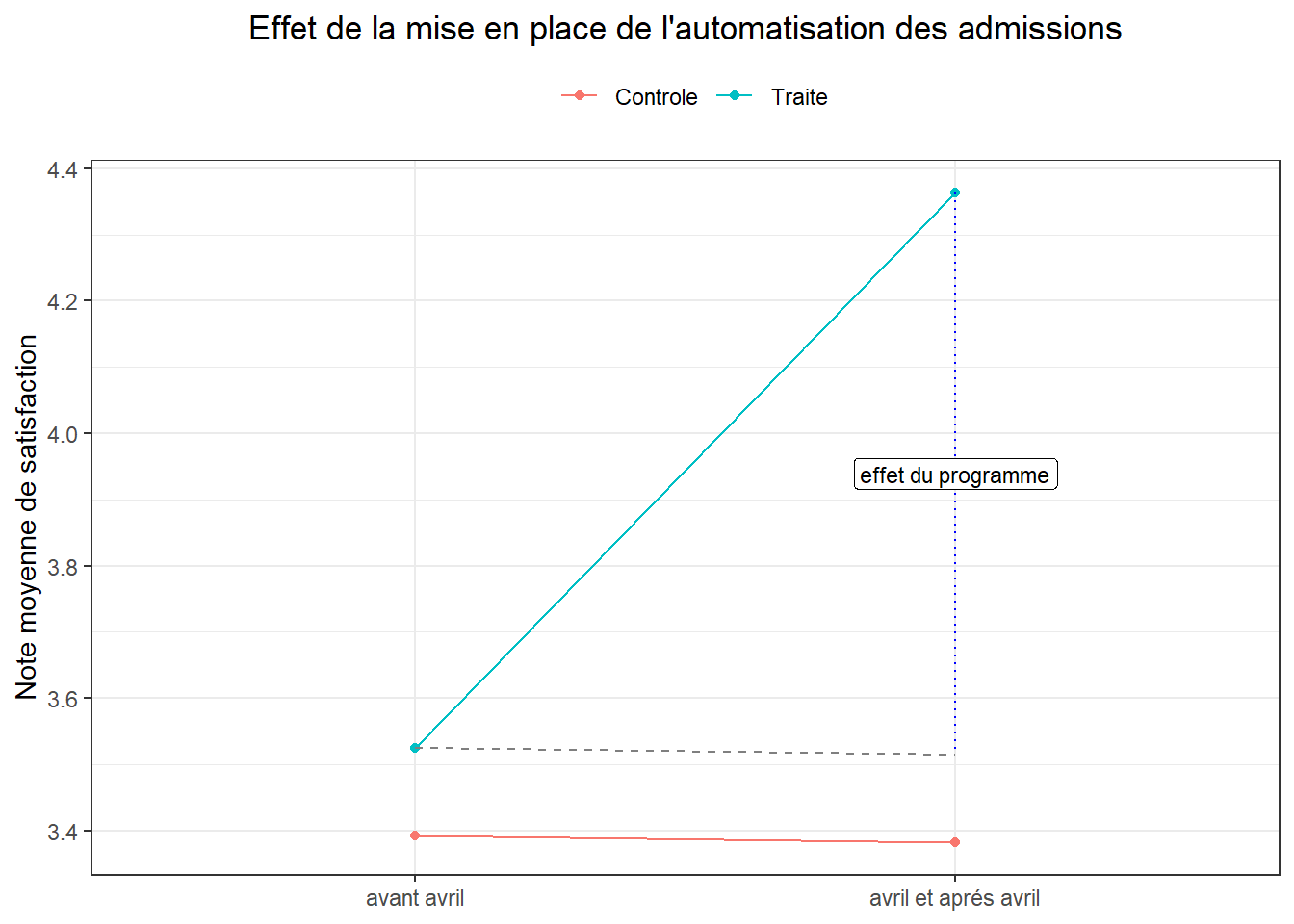
ggplot(bas_g, aes(x = post,
y = satis,
color = traite)) +
geom_point() +
geom_line(aes(group = traite)) +
labs(title="Effet de la mise en place de l'automatisation des admissions",
y="Note moyenne de satisfaction",
color="")+
annotate(geom = "segment", x = "avant avril",
xend = "avril et aprés avril",
y = bas_g$satis[3],
yend = bas_g$satis[4] - did,
linetype = "dashed", color = "grey50") +
annotate(geom = "segment", x = "avril et aprés avril",
xend = "avril et aprés avril",
y = bas_g$satis[4] ,
yend = bas_g$satis[4] - did,
linetype = "dotted", color = "blue") +
annotate(geom = "label", x = "avril et aprés avril",
y = bas_g$satis[4] - (did / 2),
label = "effet du programme", size = 3)+
theme_bw()+
theme(
plot.title = element_text(hjust=0.5),
axis.title.x = element_blank(),
legend.position = "top"
)
rm(bas_g,did)Tests complémentaires
Analyses graphiques de la parallel trend hypothesis
Examinons l’hypothèse de parallel trend. Commençons par une rapide analyse graphique. Reprenons celle développée dans le post précédant. Calculons donc les moyennes de l’outcome sur les différents mois respectivement sur le groupe des traités et des non traités (le groupe de contrôle). Créons une fonction pour faciliter les réplications qui suivront. Celle-ci doit permettre de générer un tableau présentant pour chaque mois la satisfaction moyenne sur le groupes de traités et le groupe de contrôle, ainsi que le graphe associée.
parallel_plot<-function(var1,trait,time,data,table=TRUE){
par_1<-data %>%
group_by({{trait}},{{time}}) %>%
summarise(moy_=mean({{var1}}),.groups = "keep") %>%
cbind(trait=c(rep(FALSE,7),rep(TRUE,7)))
colnames(par_1)<- c("status","month","moy_","trait")
if(table==TRUE){
par_1
}else{
ggplot(data=par_1,aes(x=month,y=moy_,
colour=trait,
shape=trait,
alpha=trait))+
geom_point()+
geom_line()+
geom_vline(xintercept = 3,
linewidth=0.1,linetype="dashed")+
geom_text(aes(label="Automatisée",
x=6,
y=4.25))+
labs(title = "Satisfaction à l'admission dans les hôpitaux",
x="mois")+
scale_x_continuous(breaks=1:7,
labels=c("Janvier","Février","Mars","Avril",
"Mai","Juin","Juillet"))+
scale_y_continuous(breaks = seq(3.2,4.4,0.2))+
scale_shape_manual(values=c(1, 16))+
scale_colour_manual(values=c("Black","Black"))+
scale_alpha_manual(values=c(0.5,1))+
theme_minimal()+
theme(
plot.title = element_text(hjust=0.5,face="bold"),
axis.title.y = element_blank(),
axis.title.x = element_blank(),
axis.line = element_line(color="black",linewidth=0.1),
axis.ticks = element_line(color="black",linewidth=0.1),
panel.grid = element_blank(),
legend.position="none")}
}Appliquons notre nouvelle fonction pour obtenir le tableau des moyennes.
parallel_plot(satis,Traite,month,dat2_)## # A tibble: 14 × 4
## # Groups: status, month [14]
## status month moy_ trait
## <chr> <dbl+lbl> <dbl> <lgl>
## 1 Controles 1 [January] 3.39 FALSE
## 2 Controles 2 [February] 3.38 FALSE
## 3 Controles 3 [March] 3.42 FALSE
## 4 Controles 4 [April] 3.40 FALSE
## 5 Controles 5 [May] 3.36 FALSE
## 6 Controles 6 [June] 3.39 FALSE
## 7 Controles 7 [July] 3.37 FALSE
## 8 Traités 1 [January] 3.53 TRUE
## 9 Traités 2 [February] 3.51 TRUE
## 10 Traités 3 [March] 3.53 TRUE
## 11 Traités 4 [April] 4.34 TRUE
## 12 Traités 5 [May] 4.38 TRUE
## 13 Traités 6 [June] 4.35 TRUE
## 14 Traités 7 [July] 4.38 TRUEGénérons le graphe pour visualiser plus nettement l’hypothèse de paralell trend pré traitement.
parallel_plot(satis,Traite,month,dat2_,table=FALSE)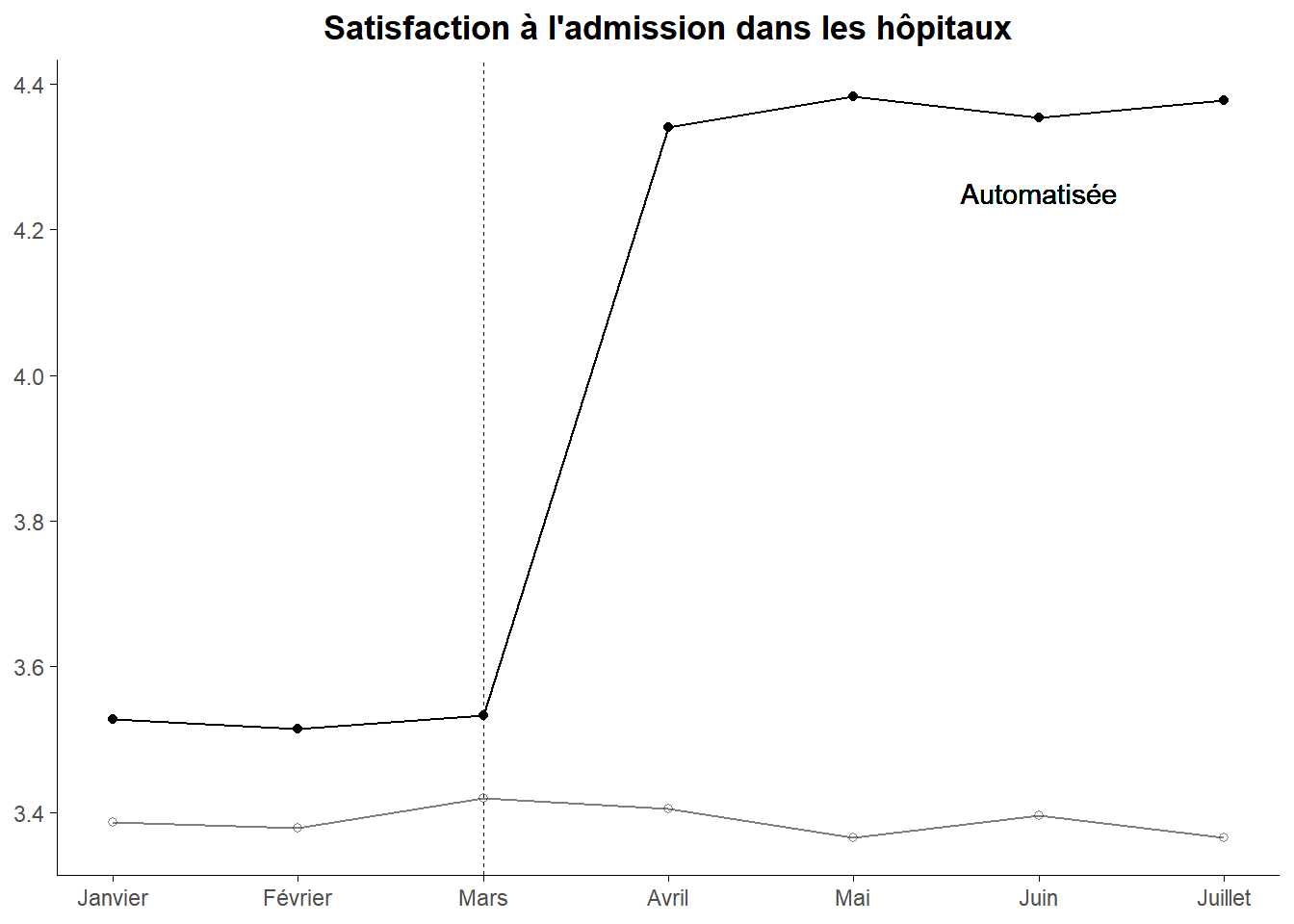
Le graphe obtenu correspond au premier généré par la fonction estat trendplots de Stata. Il s’agit d’une commande post estimation. A sa lecture, on peut dire qu’à première vue que la parallel trend pré traitement semble tenir.
Mais allons plus loin. Essayons d’établir le second graphe. Celui-ci est obtenue en commençant par unifier le départ des deux séries puis en les prolongeant à partir d’un trend linéaire. Si la parallel trend est respectée les deux séries devrait se superposer sur le période pré traitement.
Établissons donc le point de départ en faisant la moyenne des observations sur la première période d’observation.
m1<-mean(dat2_$satis[which(dat2_$month==1)])
m1## [1] 3.444675Une fois celui-ci obtenu, calculons les clés d’ajustement à pratiquer sur les deux séries (Contrôles et Traités) pour leur donner la même origine.
aj_c<-m1-mean(dat2_$satis[which(dat2_$month==1&dat2_$Traite=="Controles")])
aj_t<-m1-mean(dat2_$satis[which(dat2_$month==1&dat2_$Traite=="Traités")])
c(aj_c,aj_t)## [1] 0.05879710 -0.08259228Appliquons-les à nos données.
dat2_1<-dat2_ %>%
mutate(satis_=ifelse(Traite=="Controles",satis+aj_c,satis+aj_t))
rm(aj_c,aj_t)On peut vérifier que l’ajustement a été correctement effectué en calculant la moyen sur le premier mois de notre satisfaction ajustée.
mean(dat2_1$satis_[which(dat2_1$month==1)])## [1] 3.444675L’ajustement apparaît être correcte. Etablisons notre second graphe.
parallel_plot(satis_,Traite,month,dat2_1,table=FALSE)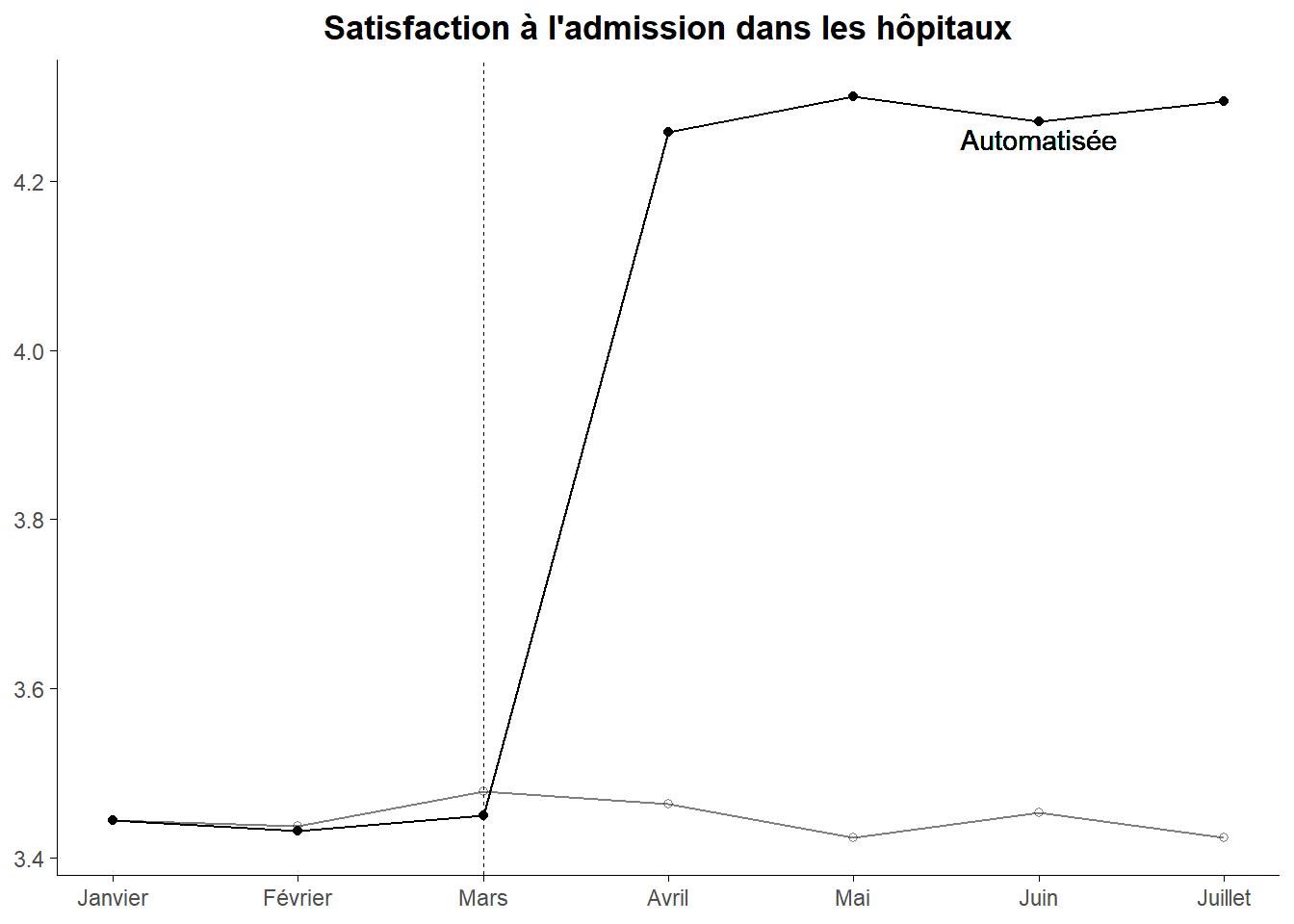
Tests statistiques de la parallel trend hypothesis
L’analyse graphique peut être appuyée par un complément statistique. Le focal est toujours porté sur la période pré traitement. La parallel trend post traitement, celle qui dans l’absolu, nous intéresse n’est pas testable. Aussi, en nous reportant à la période pré traitement, nous faisant l’hypothèse qu’elle tiendrait post traitement en l’absence de traitement…
Dans les post précédant, pour tester la parallel trend hypothesis, nous avons estimé sur la période pré traitement le modèle linéaire suivant :
\[satis=month+month×traité\]
L’outcome est régressé sur une variable marquant la progression du temps et son interaction avec la binaire marquant l’appartenance au groupe des traités.
L’idée est que, si le coefficient associé à la variable d’intéraction est statistiquement différent de 0, on doit rejeter la parallel trend dans la mesure où cela montre que le trend de l’outcome sur la groupe des traités et différents de celui sur le groupe de contrôle. Appliquons la procédure à nos données.
reg_p1<-lm(satis~month+month*Traite,
data=filter(dat2_,month<4))
coeftest(reg_p1)[4,]## Estimate Std. Error t value Pr(>|t|)
## -0.01324090 0.03888429 -0.34052052 0.73348401rm(reg_p1)Ici, on ne peut pas rejeté H0, autrement-dit les trend sur le groupe des traités et le groupe de contrôle semblent être les mêmes ce qui va dans le sens de la parallel trend.
Stata propose un test construit sur le même principe, mais en mobilisant une spécification étendue. La spécification retenue prend pour point de départ celle de la régression en Diff-in-Diff pour lui ajouter deux variables proposant une triple interaction la première entre une variable marquant la période pré, l’appartenance au groupe de traité et la période, et la seconde entre une variable marquant la période post et les mêmes variables.
On a ainsi pour une Diff-in-Diff estimé en TWFE :
\[ satis_{i,t,s}=\gamma_i+\gamma_t+D_{s,t}+\zeta_1.pre.traité.month+\zeta_2.post.traité.month+\epsilon_{i,t,s} \]
Le test porte alors sur \(\zeta_1\). Si ce coefficient est statistiquement différent de zéro, alors il y a une différence de trend entre les traités et le groupe de contrôle sur la période pré traitement. Et donc la parallel trend ne tiendrait pas. Le test pratiqué est alors un test de Wald qui établi sa statistique comme le carré du t stat ordinaire. Cette statistique, sous H0 (\(\zeta_1=0\)), suit une loi de Fisher à 1 et n-1 degré de liberté (n étant le nombre d’individu utilisé pour les effets fixes ici le nombre d’hôpitaux). Répliquons le test.
Commençons par préparer les données avant de procéder à l’estimation du modèle. Marquons les périodes pré et post traitement, établissons pour chaque hôpital s’il est traité ou non, enfin calculons les interactions triples.
dat2p<-dat2 %>%
mutate(pre=ifelse(month<4,1,0),
post=ifelse(month>3,1,0)) %>%
group_by(hospital) %>%
mutate(trait=ifelse(sum(procedure)==0,0,1)) %>%
ungroup() %>%
mutate(avant=pre*trait*month,
apres=post*trait*month)Ceci fait, on peut procéder à la régression, sortir le t stat du coefficient, l’élevé au carré et définir la p-value via la loi de Fisher a 1 et n-1 degrés de liberté. Ici, n correspond au nombre d’hôpitaux (46).
reg_2p<-lm(satis~procedure+avant+apres+factor(hospital)+factor(month),
data=dat2p)
Fish<-coeftest(reg_2p,vcov.=vcovCL(reg_2p,cluster=dat2p$hospital))[3,3]^2 %>%
round(digits = 8)
prob<-pf(Fish,1,45,lower.tail=FALSE)
c(F=Fish,pv=prob) %>% round(digits=4)## F pv
## 0.5516 0.4615rm(reg_2p,Fish,prob,dat2p)Comme précédemment on ne peut pas rejeter H0, autrement-dit on ne peut pas rejeté l’hypothèse que \(\zeta_1\) soit nulle et donc qu’il n’y ait pas de différence de trend entre les futures traités et le groupe de contrôle. L’hypothèse de parallel trend pré traitement ne peut donc pas pas être rejetée.
Cela va dans le même sens que l’analyse graphique et que notre test précédent.
Analyse graphique de la temporalité du traitement
En plus de la parallel trend (ou comme autre test de cette dernière), on peut s’interroger sur la temporalité des effets du traitement. Est-ce que la date retenue est bien celle à partir de laquelle celui-ci produit des effets? Est-ce qu’il n’y a pas d’anticipation ou de retard ce qui pourrait remettre en cause (au moins en partie) le cadre méthodologique (la parallel trend serait en partie remise en cause)? Pour le voir, on peut présenter le graphe de l’effet du traitement dans le temps (comme nous l’avons fait dans le post précédent). Autrement-dit, nous procédons à l’étude des dynamic treatement effects.
Il s’agit d’estimer dans un seul modèle, pour une série de dates, l’effet du traitement sur les traités (même s’ils n’ont pas encore été traité) via une spécification de type 2x2 Diff in Diff . Cela se concrétise par une série d’interactions entre les différentes dates retenues et la variable binaire marquant le fait d’appartenir au groupe des traités. Les dates choisies (généralement retenues) correspondent aux périodes avant l’évènement à l’exception de celle qui le précédent immédiatement (qui sera notre référence) et de l’ensemble de celles après l’évènement.
On a donc ici à estimer le modèle suivant:
\[ satis_{it}=\gamma_i+\gamma_t+\beta_1.T_{−2}.Traité+\beta_2.T_{−1}.Traité+\beta_3.T_1.Traité+\beta_4.T_2.Traité+\beta_5.T_3.Traité+\beta_6.T_4.Traité+\epsilon_{it} \]
où \(T_{−1}\) correspond à janvier, \(T_{−2}\) à février, \(T_1\) à avril, \(T_2\) à mai, etc…
Le traitement est attribué en avril, le mois 4 sur les 7 disponibles. Si on fixe la référence au mois 3, on a 2 leads (dans la mesure où ils correspondraient à des anticipations du traitement) et 4 lags (dans la mesure où ils correspondraient des effets retardés du traitement).
Pour mettre en oeuvre l’estimation, commençons par centrer nos dates autour de l’évènement en reprenant la base nous ayant permis d’estimer la 2x2 diff in diff . Celle-ci comprend la variable Traite qui indique si l’observation est issue d’un hôpital qui adoptera ou a adopté le nouveau système. Établissons la variable comme un facteur pour permettre les interactions date par date.
dat3<-dat2_ %>%
mutate(m_cent3=month-3,
m_cent3f=relevel(factor(m_cent3),ref="0"))
head(dat3)## # A tibble: 6 × 9
## # Groups: hospital [1]
## hospital frequency month procedure satis Traite post m_cent3 m_cent3f
## <dbl> <dbl+lbl> <dbl+lbl> <dbl+lbl> <dbl> <chr> <lgl> <dbl> <fct>
## 1 1 3 [High] 7 [July] 1 [New] 4.11 Trait… TRUE 4 4
## 2 1 2 [Medium] 3 [March] 0 [Old] 3.32 Trait… FALSE 0 0
## 3 1 4 [Very high] 2 [Febru… 0 [Old] 3.41 Trait… FALSE -1 -1
## 4 1 2 [Medium] 4 [April] 1 [New] 3.00 Trait… TRUE 1 1
## 5 1 1 [Low] 3 [March] 0 [Old] 3.11 Trait… FALSE 0 0
## 6 1 1 [Low] 7 [July] 1 [New] 2.88 Trait… TRUE 4 4Ceci fait il ne nous reste plus qu’à établir la régression. Ici, compte tenu du grand nombre de coefficients qui seront calculés (58), nous utiliserons la fonction feols() du package fixest pour l’estimation. Elle nous permet d’obtenir uniquement la série de coefficient qui nous intéresse. Présentons-les ainsi que les tests associés (toujours avec le clustering sur hospital).
reg_dyn <- feols(satis ~ m_cent3f*Traite |
hospital + month,
data = dat3)
coeftest(reg_dyn,vcov.=vcovCL(reg_dyn,cluster=dat3$hospital))%>%
round(digits = 7)##
## t test of coefficients:
##
## Estimate Std. Error t value Pr(>|t|)
## m_cent3f-2:TraiteTraités 0.027897 0.035431 0.7874 0.4311
## m_cent3f-1:TraiteTraités 0.021732 0.037860 0.5740 0.5660
## m_cent3f1:TraiteTraités 0.822815 0.049302 16.6895 <2e-16 ***
## m_cent3f2:TraiteTraités 0.904050 0.046786 19.3230 <2e-16 ***
## m_cent3f3:TraiteTraités 0.844724 0.060565 13.9474 <2e-16 ***
## m_cent3f4:TraiteTraités 0.897888 0.050960 17.6193 <2e-16 ***
## ---
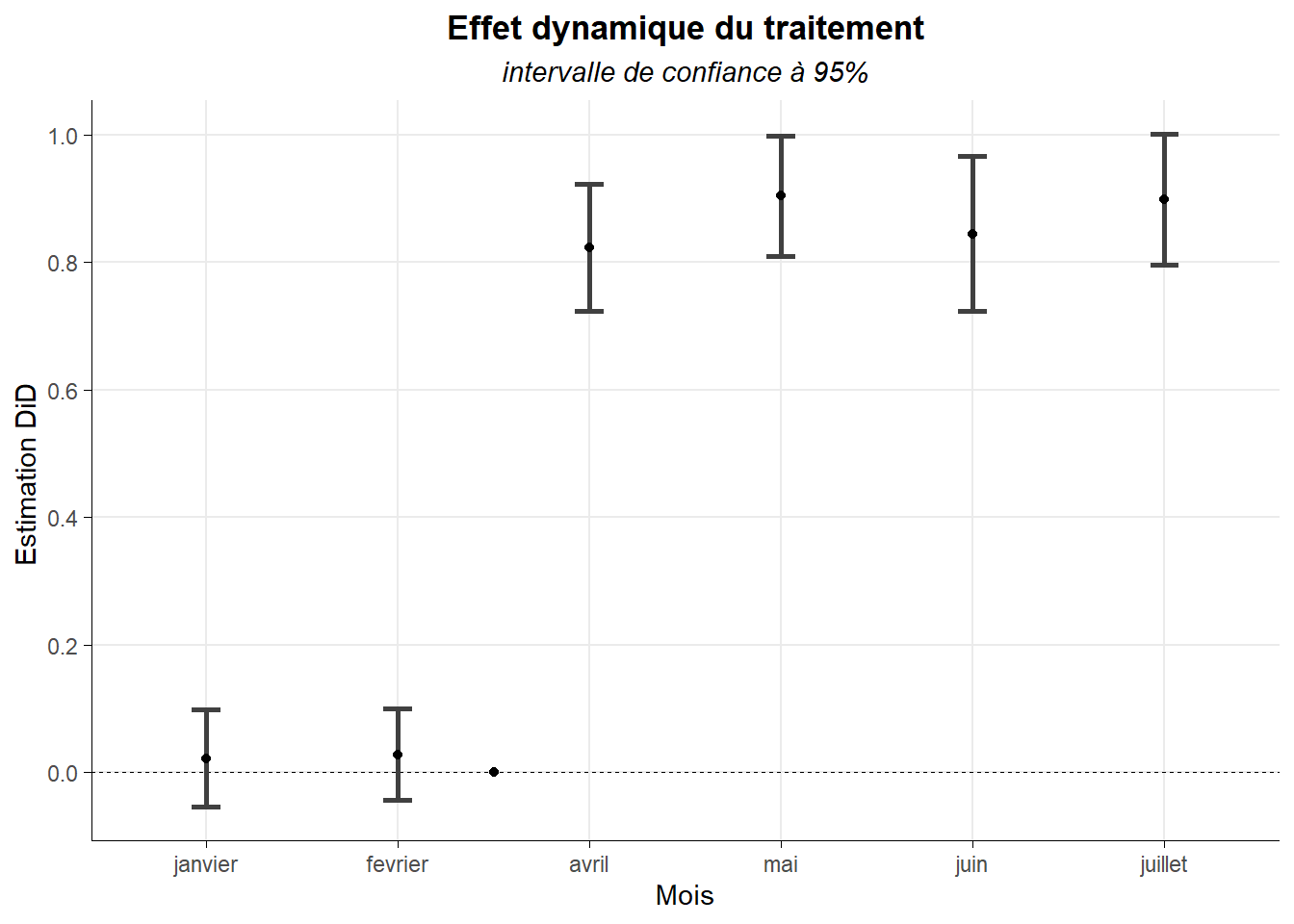
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1On constate que dans leur ensemble les coefficient des leads ne sont pas statistiquement significatifs contrairement à ceux de l’ensemble des lags. Cela confirme l’absence d’anticipation du traitement. Produisons le graphe permettant de mettre en évidence ce résultat. Celui-ci ce base sur la présentation des intervalles de confiance à 95% des coefficients des différents leads et lags. Ceux-ci peuvent simplement être obtenu à partir de la fonction coefci() du package lmtest.
coefci(reg_dyn,vcov.=vcovCL(reg_dyn,cluster=dat3$hospital),level=0.95)## 2.5 % 97.5 %
## m_cent3f-2:TraiteTraités -0.04155824 0.09735225
## m_cent3f-1:TraiteTraités -0.05248483 0.09594913
## m_cent3f1:TraiteTraités 0.72617022 0.91946035
## m_cent3f2:TraiteTraités 0.81233554 0.99576416
## m_cent3f3:TraiteTraités 0.72599932 0.96344865
## m_cent3f4:TraiteTraités 0.79799120 0.99778581Pour assembler le graphe, nous avons plusieurs possibilités (comme dans le post précédent). On peut par exemple utiliser la fonction coefplot() du package fixest ou ggcoef() du package GGally. Nous optons pour la second solution qui, comme le nom l’indique, utilise la syntaxe de ggplot.
GGally::ggcoef(reg_dyn,
errorbar_height = 0.15,
errorbar_size = 1,
vline_linetype = "dashed",
vline_color = "black",
vline_size = 0.2)+
annotate(geom="point",x=0,y=2.5)+
labs(title="Effet dynamique du traitement",
subtitle = "intervalle de confiance à 95%",
x="Estimation DiD ",
y="Mois")+
scale_y_discrete(labels=c("janvier","fevrier","avril",
"mai","juin","juillet"))+
scale_x_continuous(breaks=seq(0,1,0.2))+
coord_flip()+
theme_minimal()+
theme(
plot.title = element_text(hjust = 0.5,face="bold"),
plot.subtitle = element_text(hjust = 0.5,face="italic"),
axis.line = element_line(color="black",
linewidth=0.15),
axis.ticks = element_line(color="black",
linewidth=0.1),
panel.grid.minor = element_blank()
)
Test statistique de la temporalité du traitement
En complément avec l’analyse graphique, on peut pratiquer un test de causalité de type test de Granger pour vérifier si les effets du traitement sont observés avant sa mise en oeuvre (officielle, la date d’évènement). Sous Stata, il est pratiqué en post estimation via la commande estat granger. Répliquons la.
Le test part de la même modélisation que celle que nous avons mobilisée pour générer le graphe du dynamic treatement effects à la différence prés que seul les leads sont considérés. Il s’agira alors de tester l’hypothèse jointe (H0) que les coefficients associés sont tous égaux à 0. Cela est réalisé à partir d’un test de Wald dont la statistique suit une loi de Fisher égale au nombre de leads et au nombre de cluster moins 1.
Avant de procéder au test, créons une variable indiquant les leads, la référence et les lags.
dat3<-dat3 %>%
mutate(leads_=ifelse(m_cent3%in%c(-2,-1,0),m_cent3f,"lags"),
leads_f=relevel(factor(leads_,labels = c("0","-2","-1","lags")),
ref="0"))
head(dat3)[,c(3,8:11)]## # A tibble: 6 × 5
## month m_cent3 m_cent3f leads_ leads_f
## <dbl+lbl> <dbl> <fct> <chr> <fct>
## 1 7 [July] 4 4 lags lags
## 2 3 [March] 0 0 1 0
## 3 2 [February] -1 -1 3 -1
## 4 4 [April] 1 1 lags lags
## 5 3 [March] 0 0 1 0
## 6 7 [July] 4 4 lags lagsUne fois les données prêtes, il ne reste plus qu’à réaliser la régression. Observons-en les résultats.
reg_dyn_ <- feols(satis ~ leads_f*Traite |
hospital + month,
data = dat3)
coeftest(reg_dyn_,vcov.=vcovCL(reg_dyn_,cluster=dat3$hospital))%>%
round(digits = 7)##
## t test of coefficients:
##
## Estimate Std. Error t value Pr(>|t|)
## leads_f-2:TraiteTraités 0.027897 0.035431 0.7874 0.4311
## leads_f-1:TraiteTraités 0.021732 0.037860 0.5740 0.5660
## leads_flags:TraiteTraités 0.867369 0.042337 20.4873 <2e-16 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1Les deux coefficients associés aux leads ne sont pas statistiquement différents de zéro. Il ne semble pas y avoir d’anticiaption des effets du traitement. Néanmoins, pour aller au bout de la démarche, pratiquons le test d’hypothèse jointe sur ces coefficients (H0 les deux coefficients sont égale à 0). Pour cela, utilisons la fonction linearHypothesis() qui est issue du package car. Indiquons les hypothèses à tester et la nature de la statistique retenue (ici F pour Fisher).
linearHypothesis(reg_dyn_,c("leads_f-2:TraiteTraités = 0",
"leads_f-1:TraiteTraités = 0"),
test="F",
vcov.=vcovCL(reg_dyn_,cluster=dat3$hospital),
white.adjust="hc1")##
## Linear hypothesis test:
## leads_f-2:TraiteTraités = 0
## leads_f-1:TraiteTraités = 0
##
## Model 1: restricted model
## Model 2: satis ~ leads_f * Traite | hospital + month
##
## Note: Coefficient covariance matrix supplied.
##
## Res.Df Df F Pr(>F)
## 1 7315
## 2 7313 2 0.3278 0.7205rm(reg_dyn,reg_dyn_,dat3)Le test confirme que l’on ne peut par raisonnablement rejeter H0. Cela va dans le sens d’une absence d’effets du traitement avant la date désignée comme étant celle de sa mise en place. L’hypothèse de non anticipation semble tenir.
Pour résumer, la mise en place de l’automatisation de la procédure d’enregistrement des patients apparaît bien améliorer la satisfaction des patients. La méthode utilisée pour le mettre en évidence l’analyse en Diff in Diff (double différence) le confirme. Par ailleurs, les hypothèses sur lesquelles reposent cette méthode pour être mise en oeuvre parallel trend et non anticipation apparaissent également vérifiées.