Le(s) papier(s) d’origine

Nous nous intéressons ici à des anomalies ont été relevées sur la base de périodes définies de l’année composées d’un ou de plusieurs mois. Nous en testerons deux: l’effet janvier(/avril) et l’effet ‘sell in may and go away’ (ou Halloween).

Rozeff and Kinney (1976) sont ainsi les premiers à relever la présence de rendements anormalement élevés au moins de janvier sur le NYSE à partir d’un indice équipondéré. Le phénomène est expliqué au moins partiellement par des considérations fiscales. On peut se reporter à Thaler (1987) pour une synthèse des discutions autour de ce résultat à l’époque (reposant sur les plus petites capitalisations, les titres qui ont précédemment sous-performé, avec des rendement fort positif concentrés sur les premiers jours du mois…). L’anomalie a été documenté dans de nombreux pays. Au Royaume-Uni, la période fiscale est en avril pourtant l’effet janvier y a été documenté.

Bouman and Jacobsen (2002) mettent en évidence la présence d’une période plus fréquemment baissière sur les marchés situées entre mai et septembre, voir entre mai et octobre confirmant l’adage comme quoi il faudrait mieux vendre ses actions en mai et ne revenir sur le marché qu’après Halloween.

Chargeons les packages et les données

Pour tester les effets janvier et ‘sell in may’ , nous ne mobiliserons ici quelques packages : le très classique tidyverse et scale qui nous permettra de mettre en forme les axes de nos graphes. Chargeons-les.

library(tidyverse)
library(scales)

Ceci étant fait, chargeons les données sur lesquelles nous allons testons les anomalies. Il s’agit encore une fois des rendements de l’indice Standard & Poor 500 (encore une fois vous pouvez le faire ici). La période de test retenue est ici celle courant du 31 décembre 1959 au 31 décembre 2020.

dat<-read_delim("S&P500_return.csv",delim=";") %>%
  filter(date_t>=as.Date('1959-12-31',"%Y-%m-%d")&
           date_t<=as.Date('2020-12-31',"%Y-%m-%d"))

head(dat)

## # A tibble: 6 × 3
##   date_t     SP500       ret
##   <date>     <dbl>     <dbl>
## 1 1959-12-31  59.9  0.00201 
## 2 1960-01-04  59.9  0.000334
## 3 1960-01-05  60.4  0.00801 
## 4 1960-01-06  60.1 -0.00431 
## 5 1960-01-07  59.7 -0.00732 
## 6 1960-01-08  59.5 -0.00318

Traitement des données

Marquons les mois et périodes que nous allons mobilisés pour les tests. Commençons par les mois de janvier et d’avril, pour l’effet janvier ou équivalent. Ajoutons la période de l’année qui n’est pas située entre mai et octobre et donc celle qui coure entre courant d’octobre à mai (avant mai et après octobre). Si les effets existent (encore), nous devrions constaté des rendements en moyenne plus élevés en janvier (et ou avril) que sur les autres mois et sur la période composée des mois de octobre, novembre, décembre, janvier, février, mars, avril et mai (avant mai et après octobre).

dat<-dat %>%
  mutate(mois=month(date_t),
         mois_l=month(date_t,label=TRUE),
         janv=mois==1, avr=mois==4,
         hallowen=ifelse(mois<=5,1,ifelse(mois>=10,1,0)))

Statistiques descriptives

Avant d’entrer dans le vif de l’analyse présentons quelques éléments descriptifs. Commençons par calculer les rendements journaliers moyens pour chaque mois.

tab<-dat %>%
  group_by(mois_l) %>%
  summarize(mois=unique(mois),
            N=n(),
            moyenne=round(mean(ret),digits=6)) %>%
  ungroup() 

tab

## # A tibble: 12 × 4
##    mois_l  mois     N   moyenne
##    <ord>  <dbl> <int>     <dbl>
##  1 janv       1  1274  0.000501
##  2 févr       2  1168  0.000023
##  3 mars       3  1333  0.000444
##  4 avr        4  1260  0.000757
##  5 mai        5  1291  0.000092
##  6 juin       6  1303 -0.000005
##  7 juil       7  1282  0.000341
##  8 août       8  1348  0.000118
##  9 sept       9  1237 -0.000289
## 10 oct       10  1344  0.000424
## 11 nov       11  1232  0.000794
## 12 déc       12  1284  0.000656

Présentons ces éléments sous la forme d’un graphe. Marquons en bleu la moyenne des rendements journaliers moyens de chaque mois et en rouge les rendements nuls.

ggplot(data=tab,aes(x=mois,y=moyenne))+
  geom_line()+
  geom_point()+
  geom_hline(yintercept = 0,color='red')+
  geom_hline(yintercept = mean(tab$moyenne),color='blue')+
  annotate("text",label="moyenne",
           x=11,
           y=mean(tab$moyenne)+0.00004, color='blue')+
  labs(y="rendements moyens")+
  scale_x_continuous(breaks = 1:12,labels=tab$mois_l)+
  scale_y_continuous(labels=label_percent())+
  theme_minimal()+
  theme( 
    axis.title.x = element_blank(),
    panel.grid.minor = element_blank())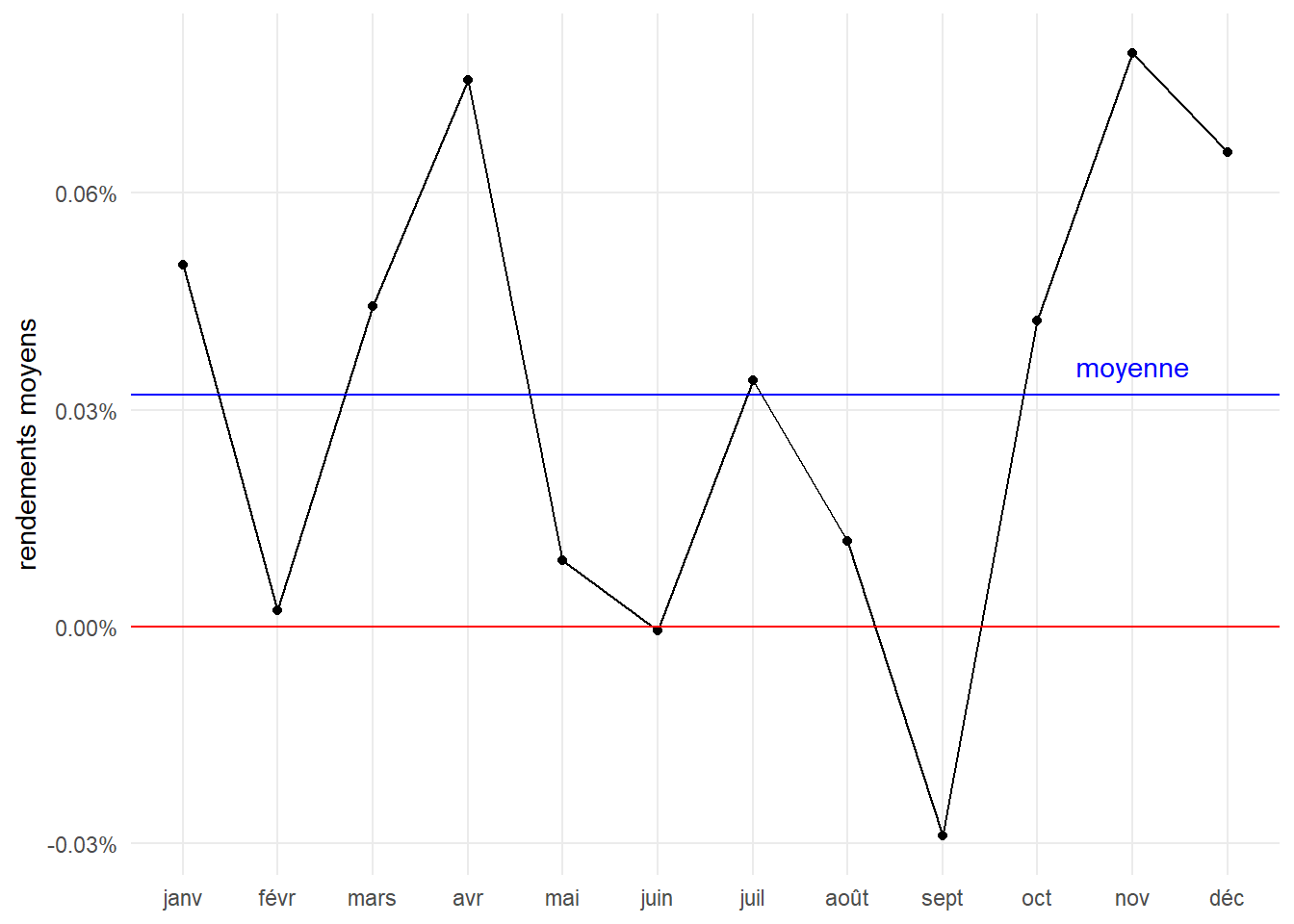

Le graphe marque la présente de rendements moyennes supérieurs sur les périodes d’intérêts. Ils sont plus fréquemment au dessus de la moyenne générale. Néanmoins, cela ne dit pas si ces différences sont statistiquement significatives. Procédons au test.

Tests statistiques

Commençons par tester l’effet janvier (et avril) qui se justifierait par des périodes fiscales (liquidation des positions perdante en décembre pour matérialiser les moins-values avant le redémarrage de l’année fiscale de manière à réduire l’impôt à payer et le rachat des titres concernés début janvier). Régressons les rendements journaliers sur les variables marquant les mois test (janvier et avril).

reg<-summary(lm(ret~janv+avr,data=dat))

reg

## 
## Call:
## lm(formula = ret ~ janv + avr, data = dat)
## 
## Residuals:
##       Min        1Q    Median        3Q       Max 
## -0.204931 -0.004531  0.000128  0.004769  0.115538 
## 
## Coefficients:
##              Estimate Std. Error t value Pr(>|t|)   
## (Intercept) 2.620e-04  9.047e-05   2.896  0.00378 **
## janvTRUE    2.390e-04  3.009e-04   0.794  0.42714   
## avrTRUE     4.948e-04  3.025e-04   1.636  0.10184   
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 0.01024 on 15353 degrees of freedom
## Multiple R-squared:  0.0002018,	Adjusted R-squared:  7.155e-05 
## F-statistic: 1.549 on 2 and 15353 DF,  p-value: 0.2124

Aucun des deux coefficients attachés à janvier et avril n’est statistiquement significatif. On ne peut donc pas sur la période conclure à la présence d’une anomalie calendaire de type effet janvier (ou même avril).

Testons la seconde anomalie :‘sell in may and go away’ (vendre en mai et revenir sur le marché après Halloween). Régressons nos rendements journaliers sur la variable marquant la période avant mai et après Halloween (octobre à avril).

reg<-summary(lm(ret~hallowen,data=dat))

reg

## 
## Call:
## lm(formula = ret ~ hallowen, data = dat)
## 
## Residuals:
##       Min        1Q    Median        3Q       Max 
## -0.205133 -0.004534  0.000142  0.004780  0.115337 
## 
## Coefficients:
##              Estimate Std. Error t value Pr(>|t|)  
## (Intercept) 4.483e-05  1.425e-04   0.315   0.7530  
## hallowen    4.185e-04  1.749e-04   2.393   0.0167 *
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 0.01024 on 15354 degrees of freedom
## Multiple R-squared:  0.0003727,	Adjusted R-squared:  0.0003076 
## F-statistic: 5.725 on 1 and 15354 DF,  p-value: 0.01674

On a un coefficient positif et statistiquement significatif (au seuil de 5%). Il apparaît que l’anomalie persiste sur la période étudiée. Les rendements journaliers sont, en moyenne, plus important entre octobre et mai qu’entre mai et octobre.

Résumons: on peut conclure que l’effet janvier ne semble plus pouvoir être mesuré sur la période d’étude. Néanmoins, notons que notre test s’éloigne des conditions dans lesquelles il a été initialement mesuré. L’indice S&P 500 est un indice pondéré par les capitalisations alors que dans le papier de Rozeff et Kinney l’indice utilisé était équipondèré. Dans un indice pondéré par les capitalisations le poids des petites capitalisation est faibles. Hors, c’est sur elles que l’effet a été documenté. Ainsi, nos conclusion ici sont mitigés: soit l’effet a été maintenant arbitré, soit notre test est trop éloigné de la configuration initiale pour être valable.

Concernant l’effet ‘sell in may’, le test est plus conforme à l’original. Il montre que l’anomalie semble persister même s’il n’est statistiquement significatif qu’au seuil de 5%. Sur la période d’étude, il ne semble pas être arbitré (ou du moins pleinement arbitré).