Dans ce troisième post de la série sur la finance comportementale, nous abordons une autre anomalie calendaire détectée sur les marchés. Les sources et inspirations sont les mêmes que pour les post précédents (la chaîne Youtube NEDL) .
Le(s) papier(s) d’origine
L’effet fin de mois/début de mois (turn of the month effect) est une autre anomalie de marché au regard de l’hypothèse d’efficience détecté dans les années 80. Elle repose sur le constat que rendements les plus importants sont concentrés autour du passage d’un mois à l’autre (les tout débuts et fins de mois). Elle a été mesurée pour la première fois par Ariel (1987) et Lakonishok and Smidt (1988). Pour Ariel, il s’agit des deux premières semaines du mois et du dernier jours du mois. Pour Lakonishok et Smidt, il s’agit des trois premiers jours du mois et des quatre derniers.
Des justifications de l’effet associés à l’épargne des rémunérations perçues à rythme mensuel ont pu être mis en avant avec plus ou moins de succès.
Chargeons les packages et les données
Pour tester l’effet fin de mois/debut (turn of the month effect), nous ne mobiliserons ici quelques packages : zoo qui permet de traiter facilement des données à la structure temporelles, le très classique tidyverse et scale qui nous permettra de mettre en forme les axes de nos graphes. Chargeons-les.
library(zoo)
library(tidyverse)
library(scales)Ceci étant fait, chargeons les données sur lesquelles, nous allons tester l’effet. Il s’agit encore une fois des rendements de l’indice Standard & Poor 500 (encore une fois vous pouvez les charger ici). La période de test retenue est celle courant du 31 décembre 1959 au 31 décembre 2020.
dat<-read_delim("S&P500_return.csv",delim=";") %>%
filter(date_t>=as.Date('1959-12-31',"%Y-%m-%d")&
date_t<=as.Date('2020-12-31',"%Y-%m-%d"))## Rows: 23948 Columns: 3
## ── Column specification ────────────────────────────────────────────────────────
## Delimiter: ";"
## dbl (2): SP500, ret
## date (1): date_t
##
## ℹ Use `spec()` to retrieve the full column specification for this data.
## ℹ Specify the column types or set `show_col_types = FALSE` to quiet this message.head(dat)## # A tibble: 6 × 3
## date_t SP500 ret
## <date> <dbl> <dbl>
## 1 1959-12-31 59.9 0.00201
## 2 1960-01-04 59.9 0.000334
## 3 1960-01-05 60.4 0.00801
## 4 1960-01-06 60.1 -0.00431
## 5 1960-01-07 59.7 -0.00732
## 6 1960-01-08 59.5 -0.00318Traitement des données
Commençons par identifier les différents mois et couples mois-années de manière à positionner plus facilement par la suite nos périodes de fins et de débuts de mois. Pour cela, nous utilisons la fonction month() de lubridate (qui inclus dans le tidyverse) qui donne le numéro du mois (1 pour janvier…12 pour décembre) et la fonction as.yearmon() de zoo qui indique le couple mois-année.
dat_<-dat %>%
mutate(mois=month(date_t),
m_y=as.yearmon(date_t, "%Y %m"))
head(dat_)## # A tibble: 6 × 5
## date_t SP500 ret mois m_y
## <date> <dbl> <dbl> <dbl> <yearmon>
## 1 1959-12-31 59.9 0.00201 12 déc. 1959
## 2 1960-01-04 59.9 0.000334 1 janv. 1960
## 3 1960-01-05 60.4 0.00801 1 janv. 1960
## 4 1960-01-06 60.1 -0.00431 1 janv. 1960
## 5 1960-01-07 59.7 -0.00732 1 janv. 1960
## 6 1960-01-08 59.5 -0.00318 1 janv. 1960Complétons l’ensemble en numérotant les jours ouvrés (ceux pour lesquels nous avons de l’information) au sein de chaque mois.
dat_<-dat_ %>% group_by(m_y) %>%
mutate(day_of_m=1:length(m_y))
head(dat_)## # A tibble: 6 × 6
## # Groups: m_y [2]
## date_t SP500 ret mois m_y day_of_m
## <date> <dbl> <dbl> <dbl> <yearmon> <int>
## 1 1959-12-31 59.9 0.00201 12 déc. 1959 1
## 2 1960-01-04 59.9 0.000334 1 janv. 1960 1
## 3 1960-01-05 60.4 0.00801 1 janv. 1960 2
## 4 1960-01-06 60.1 -0.00431 1 janv. 1960 3
## 5 1960-01-07 59.7 -0.00732 1 janv. 1960 4
## 6 1960-01-08 59.5 -0.00318 1 janv. 1960 5Ceci fait, notons que le 31 décembre 1959 est indexé comme le jour 1 du mois alors qu’il en est le dernier. Supprimons-le de la base pour éviter cette erreur.
dat_<-dat_ %>%
filter(date_t!=as.Date('31-12-1959',format="%d-%m-%Y"))
head(dat_)## # A tibble: 6 × 6
## # Groups: m_y [1]
## date_t SP500 ret mois m_y day_of_m
## <date> <dbl> <dbl> <dbl> <yearmon> <int>
## 1 1960-01-04 59.9 0.000334 1 janv. 1960 1
## 2 1960-01-05 60.4 0.00801 1 janv. 1960 2
## 3 1960-01-06 60.1 -0.00431 1 janv. 1960 3
## 4 1960-01-07 59.7 -0.00732 1 janv. 1960 4
## 5 1960-01-08 59.5 -0.00318 1 janv. 1960 5
## 6 1960-01-11 58.8 -0.0123 1 janv. 1960 6Statistiques descriptives
Pour avoir une idée de la présence ou non de l’effet, procédons à une analyse descriptive rapide. Commençons par calculer les rendements moyens de chaque jours du mois.
tab<-dat_ %>% group_by(day_of_m) %>%
summarise(n=n(),
moy=round(mean(ret),digits=6))
tab## # A tibble: 23 × 3
## day_of_m n moy
## <int> <int> <dbl>
## 1 1 732 0.00126
## 2 2 732 0.000914
## 3 3 732 0.00103
## 4 4 732 0.000258
## 5 5 732 -0.000155
## 6 6 732 0.000119
## 7 7 732 0.000249
## 8 8 732 -0.000037
## 9 9 732 0.000488
## 10 10 732 0.000312
## # ℹ 13 more rowsLe tableau est un peu long (23 lignes). Passons le données dans un graphe plus lisible avec en ordonnées les rendements moyennes et en abscisses l’indication des jours correspondant.
ggplot(data=tab,aes(x = day_of_m, y=moy))+
geom_line()+
geom_hline(yintercept = 0,color='red')+
labs(x='Jours ouvré dans le mois',y='Rendement moyen')+
scale_x_continuous(breaks = 1:23)+
scale_y_continuous(labels = label_percent())+
coord_cartesian(expand=FALSE,ylim=c(-0.001,0.0024))+
theme_minimal()+
theme(
panel.grid.minor = element_blank()
)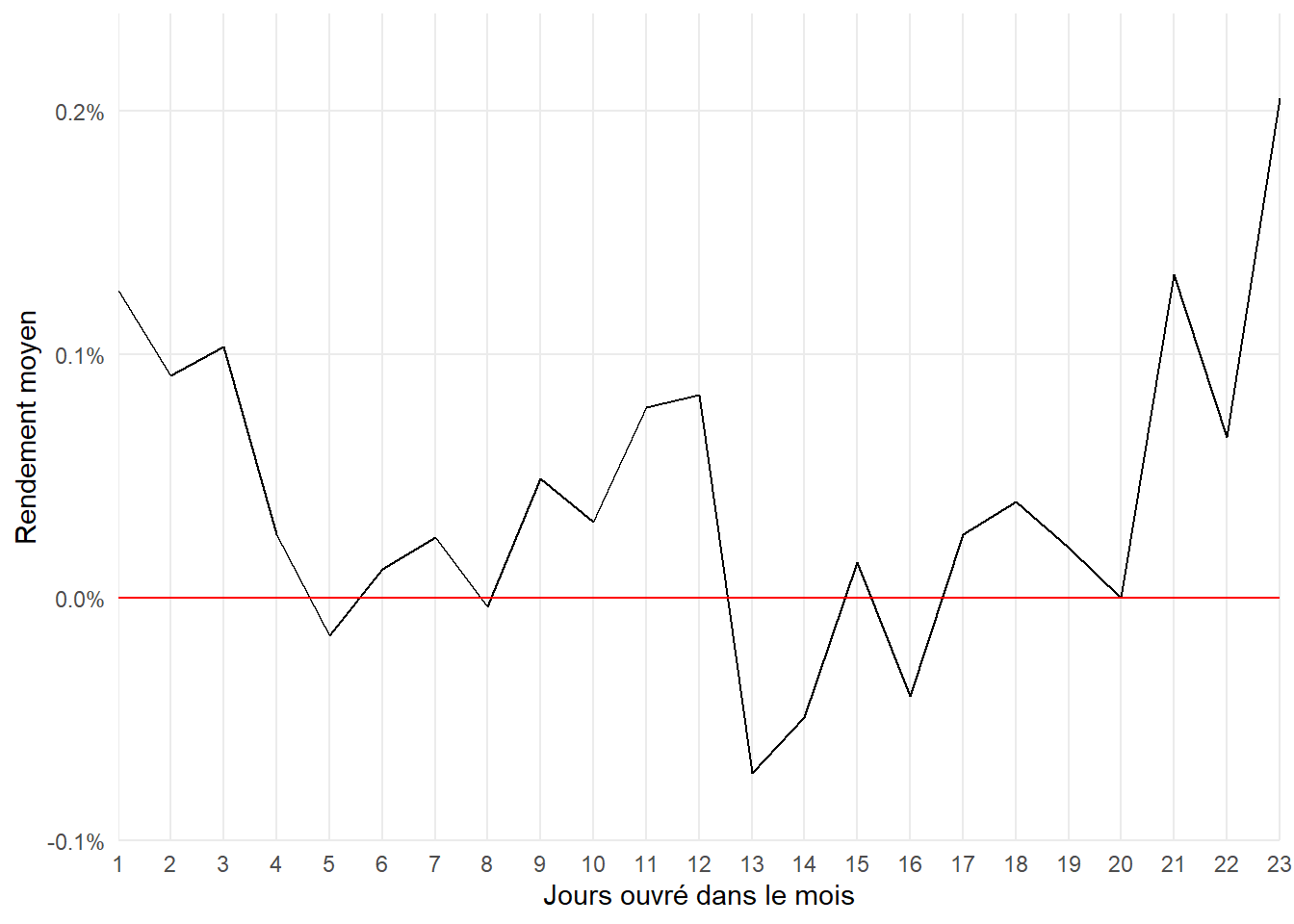
On voit bien que les rendements sont plus importants en début et en fin de mois. Mais, cette tendance est-elle statistiquement significative?
Codage des variables indicatives des jours de début et fin de mois
Commençons par les jours désignés comme début et fin de mois par Lakonishok et Smidt : les 3 premiers et les 4 dernier. Stockons l’information nécessaire au teste dans une data frame dédiée nommée dat_LS.
dat_LS<-dat_ %>%
mutate(w=ifelse(day_of_m<4,1,ifelse(lead(mois,4)==mois,0,1)),
TOM=ifelse(is.na(w)==TRUE|w==1,1,0)) %>%
select(-w)Créons de même une data frame, nommée dat_AR, intégrant le marquage des jours retenus par Ariel : les deux premières semaines (10 premiers jours) et le dernier.
dat_AR<-dat_ %>%
mutate(w=ifelse(day_of_m<=10,1,ifelse(lead(mois,1)==mois,0,1)),
TOM=ifelse(is.na(w)==TRUE|w==1,1,0)) %>%
select(-w)Tests statistiques
Pour réaliser le test, nous mobilisons une régression linéaire. Celle-ci nous permet d’obtenir le rendement moyen des jours qui ne sont pas considérés comme des début et fin de mois (la constante) et la différence entre ce rendement et celui des jours considérés comme des début et fin de mois (le coefficient).
summary(lm(ret~TOM,data=dat_LS))##
## Call:
## lm(formula = ret ~ TOM, data = dat_LS)
##
## Residuals:
## Min 1Q Median 3Q Max
## -0.204711 -0.004547 0.000144 0.004785 0.115758
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 4.215e-05 1.012e-04 0.416 0.677
## TOM 8.396e-04 1.752e-04 4.792 1.67e-06 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 0.01024 on 15353 degrees of freedom
## Multiple R-squared: 0.001493, Adjusted R-squared: 0.001428
## F-statistic: 22.96 on 1 and 15353 DF, p-value: 1.667e-06Les rendements les jours ordinaires ne sont pas statistiquement différents de zéro et les rendements des jours considérés comme début et fin de mois sont plus importants d’un peu plus de 0,0008 et par contre lui statistiquement différents de 0. C’est résultat correspondent à une moyenne des rendements journaliers sur les jours marquant le tournant des mois de 0,0881% (la somme de la constante et du coefficient) contre 0 en moyenne pour les autres jours.
Passons au test des jours désignés par Ariel. La spécification est identique.
summary(lm(ret~TOM,data=dat_AR))##
## Call:
## lm(formula = ret ~ TOM, data = dat_AR)
##
## Residuals:
## Min 1Q Median 3Q Max
## -0.204830 -0.004547 0.000146 0.004769 0.115331
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 0.0001603 0.0001199 1.337 0.181
## TOM 0.0003090 0.0001655 1.866 0.062 .
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 0.01024 on 15353 degrees of freedom
## Multiple R-squared: 0.0002269, Adjusted R-squared: 0.0001617
## F-statistic: 3.484 on 1 and 15353 DF, p-value: 0.06199La moyenne des rendements pour les jours ordinaires est également non statistiquement différente de zéro. Sur les jours désignés comme faisant partie du tournant du mois, elle est plus élevé de 0,003 points et la différence statistiquement significative mais seulement au seuil de 10% (le résultat est donc à prendre avec des pincettes). Le rendement moyenne de ces jours est de 0,04693% (somme de la constante et du coefficient).
Résumons: on peut conclure que les rendements autour des jours de début et fin de mois sont, sur la période étudiée, statistiquement différents de ceux constatés les autres jours. Il n’y a un effet tournant du mois qui peut être observé particulièrement si on retient la spécification de Lakonishok et Smidt. Les choses sont moins nettes avec les jours désignés par Ariel.
Il ne semble pas que l’anomalie ait été arbitrée.