L’objet de cette note “rapide” est de reprendre et d’approfondir (ou au moins de détailler) l’illustration de la méthode Difference-in-Difference présentée par Andrew Heiss dans son cours sur l’évaluation de programme. Vous pouvez le retrouvez à l’adresse suivante: Andrew_Heiss_Program_Evaluation_Georgia_State_University_2020.
Il s’agit du cas le plus simple: une difference-in-difference sur deux groupes (simple diff-in-diff ou 2x2 diff-in-diff). L’exemple porte sur une réforme conduite par l’Etat du Kentucky en 1980. Elle concerne le nombre maximum de semaines d’indemnisations prises en charge en cas d’accident du travail. Elle augmente cette limite. Cette réforme affecte uniquement les travailleurs à haut revenu. Ils constituent donc ici le groupe traité. Les travailleurs considérés comme à bas revenu, ceux pour qui la réforme ne change rien, sont le groupe de contrôle. La question est de savoir si cette réforme conduit les travailleurs qui en bénéficient (ceux à haut revenu) à rester plus longtemps inactifs.
Chargement et mise en forme des données
Avant d’entrer dans l’analyse des données, chargeons la série des packages qui seront mobilisés par la suite.
library(tidyverse)
library(scales)
library(broom)
library(modelsummary)Les données utilisées sont disponibles ici. Téléchargeons-les dans notre dossier de travail et chargeons-les dans notre environnement.
dat<-read_csv("data/injury.csv")Jetons un œil à ce que l’on obtient.
glimpse(dat)## Rows: 7,150
## Columns: 30
## $ durat <dbl> 1, 1, 84, 4, 1, 1, 7, 2, 175, 60, 29, 30, 100, 4, 2, 1, 1, 2,…
## $ afchnge <dbl> 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1…
## $ highearn <dbl> 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1…
## $ male <dbl> 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 0, 1, 1, 1, 1, 1…
## $ married <dbl> 0, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 0, 1, 1, 1, 1, 1…
## $ hosp <dbl> 1, 0, 1, 1, 0, 0, 0, 1, 1, 1, 0, 1, 1, 0, 0, 0, 0, 0, 1, 1, 0…
## $ indust <dbl> 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 1, 1…
## $ injtype <dbl> 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1…
## $ age <dbl> 26, 31, 37, 31, 23, 34, 35, 45, 41, 33, 35, 25, 39, 27, 24, 2…
## $ prewage <dbl> 404.9500, 643.8250, 398.1250, 527.8000, 528.9375, 614.2500, 5…
## $ totmed <dbl> 1187.57324, 361.07855, 8963.65723, 1099.64832, 372.80188, 211…
## $ injdes <dbl> 1010, 1404, 1032, 1940, 1940, 1425, 1110, 1207, 1425, 1010, 1…
## $ benefit <dbl> 246.8375, 246.8375, 246.8375, 246.8375, 211.5750, 176.3125, 2…
## $ ky <dbl> 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1…
## $ mi <dbl> 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0…
## $ ldurat <dbl> 0.0000000, 0.0000000, 4.4308167, 1.3862944, 0.0000000, 0.0000…
## $ afhigh <dbl> 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1…
## $ lprewage <dbl> 6.003764, 6.467427, 5.986766, 6.268717, 6.270870, 6.420402, 6…
## $ lage <dbl> 3.258096, 3.433987, 3.610918, 3.433987, 3.135494, 3.526361, 3…
## $ ltotmed <dbl> 7.079667, 5.889095, 9.100934, 7.002746, 5.921047, 5.351953, 4…
## $ head <dbl> 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1…
## $ neck <dbl> 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0…
## $ upextr <dbl> 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0…
## $ trunk <dbl> 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0…
## $ lowback <dbl> 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0…
## $ lowextr <dbl> 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0…
## $ occdis <dbl> 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0…
## $ manuf <dbl> 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 1…
## $ construc <dbl> 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0…
## $ highlpre <dbl> 6.003764, 6.467427, 5.986766, 6.268717, 6.270870, 6.420402, 6…On a 7,150 observations pour 30 variables. Les noms des variables ne sont pas toujours très clairs et toutes ne nous intéressent pas. Précédons donc à quelques opérations de trie et de mise en forme.
Commençons par ne garder que les informations concernant le Kentucky. La variable ky indique si l’ observation considérée est ou non faite dans cet Etat. Elle prend la valeur 1 dans ce cas là 0 si non. Une fois le tri réalisé, ne gardons que les variables centrales dans l’analyse : les différentes formes de la variable d’output (durat et ldurat); la variable afcnge, qui positionne les observations par rapport au moment où le traitement est dispensé (elle prend la valeur 0 avant et 1 aprés); la variable highearn, qui indique si les individus considérés font (égale 1) ou non (égale 0) partis du groupe des traités. Profitons également de l’occasion pour leur donner une forme plus parlante en vue de l’analyse.
dk<-dat %>%
filter(ky==1) %>%
select(durat,ldurat,afchnge,highearn) %>%
rename(duree=durat,log_duree=ldurat) %>%
mutate(
traite=factor(highearn,labels=c("Bas_revenu","Haut_revenu")),
post=factor(afchnge,labels=c("Avant_1980","Après_1980")))Examinons rapidement les premières valeurs de la base.
head(dk)## # A tibble: 6 × 6
## duree log_duree afchnge highearn traite post
## <dbl> <dbl> <dbl> <dbl> <fct> <fct>
## 1 1 0 1 1 Haut_revenu Après_1980
## 2 1 0 1 1 Haut_revenu Après_1980
## 3 84 4.43 1 1 Haut_revenu Après_1980
## 4 4 1.39 1 1 Haut_revenu Après_1980
## 5 1 0 1 1 Haut_revenu Après_1980
## 6 1 0 1 1 Haut_revenu Après_1980Analyse exploratoire
Avant/après pour tout le monde
Calculons la durée moyenne d’arrêt de travail avant et après la réforme et voyons si leur différence et statistiquement significative. Nous réaliserons cette opération plusieurs fois. Créons donc une fonction pour nous simplifier la vie.
dif_mean_t<-function(x,gr,dat){
attach(dat, warn.conflicts = FALSE)
t<-t.test(x~gr,data=dat)
vect_t<-round(c(t$estimate,t$estimate[2]-t$estimate[1],
t$statistic,p.value=t$p.value),
digits=3)
n1<-names(t$estimate) %>% str_sub(start = 15)
names(vect_t)<-c(n1,"diff","t","p.value")
round(c(vect_t),digits=3)
}Maintenant que nous avons la fonction, appliquons-la à nos données.
dif_mean_t(duree,post,dat=dk)## Avant_1980 Après_1980 diff t p.value
## 8.330 9.567 1.237 -2.125 0.034La durée moyenne du temps d’arrêt après la réforme est plus grande pour l’échantillon global. La différence est statistiquement significative au seuil de 5%.
Les mêmes résultats peuvent être obtenus au travers une régression.
reg_naive1<-lm(duree~post,data = dk)
tidy(reg_naive1) %>%
mutate_if(is.numeric, round , digits=3)## # A tibble: 2 × 5
## term estimate std.error statistic p.value
## <chr> <dbl> <dbl> <dbl> <dbl>
## 1 (Intercept) 8.33 0.401 20.8 0
## 2 postAprès_1980 1.24 0.581 2.13 0.033La constante nous donne ici la moyenne avant 1980 ( 8,330 semaines d’arrêt).
Pour avoir la moyenne après 1980, il suffit d’additionner la constante avec le coefficient de la dummy post (8,330 + 1,237 = 9,567).
sum(reg_naive1$coefficients) %>% round(digits = 3)## [1] 9.567On a une augmentation moyenne de 1,237 semaines (le coefficient de la variable d’interaction).
Observons les différences de manière plus précise au travers d’une analyse graphique.
Histogramme
Commençons par travailler à partir d’un histogramme. Dans la mesure où nous allons utiliser cette représentation plusieurs fois, établissons une fonction pour nous simplifier la vie.
hist_var<-function(x,dat,tit="",sub="",lx="",ly="",
biw){
ggplot(data=dat,aes(x=x))+
geom_histogram(binwidth=biw,color="black",boundary=0,
linewidth=0.1)+
labs(title=tit,
subtitle = sub,
x=lx,
y=ly)+
theme_bw()+
theme(
plot.title = element_text(face="bold",hjust=0.5),
plot.subtitle = element_text(face="italic",hjust=0.5)
)
}Appliquons notre fonction sur la variable durée pour l’ensemble de l’échantillon et marquons la moyenne par une ligne verticale.
hist_var(dk$duree,dk,biw=4,
tit="Distribution du nombre de semaines d'arrêt",
sub= "au Kentucky sur toute la période",
lx="Nb. de sem.",
ly="Nb. d'obs.")+
geom_vline(aes(xintercept = mean(duree), group = post),
colour = 'red')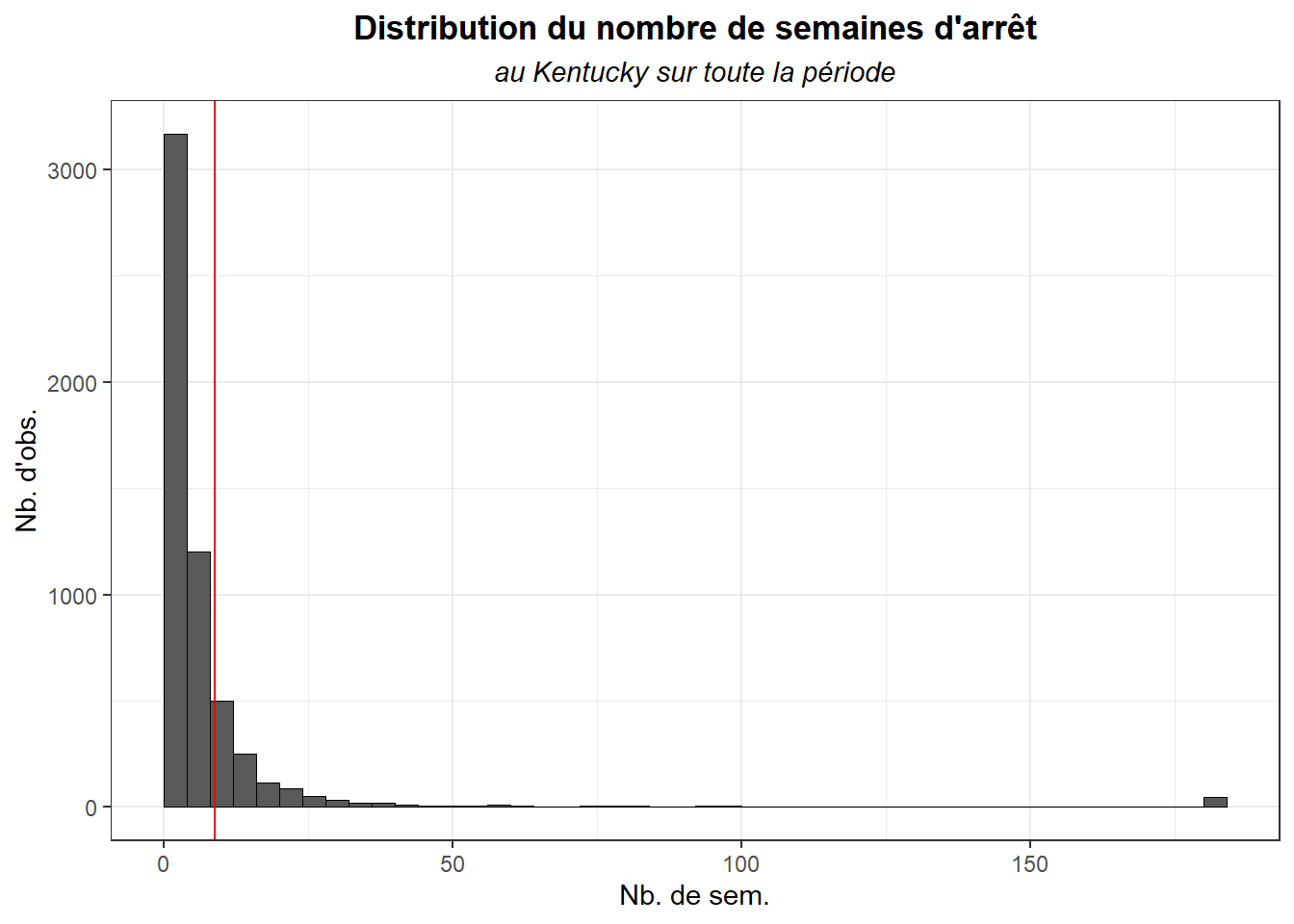
On note que la distribution est nettement asymétrique.
Voyons maintenant les différences avant et après la réforme (1980).
hist_var(dk$duree,dk,biw=4,
tit="Distribution du nombre de semaines d'arrêt",
sub= "au Kentucky sur toute la période",
lx="Nb. de sem.",
ly="Nb. d'obs.")+
facet_grid(.~post)+
geom_vline(aes(xintercept = mean(duree), group = post),
colour = 'red')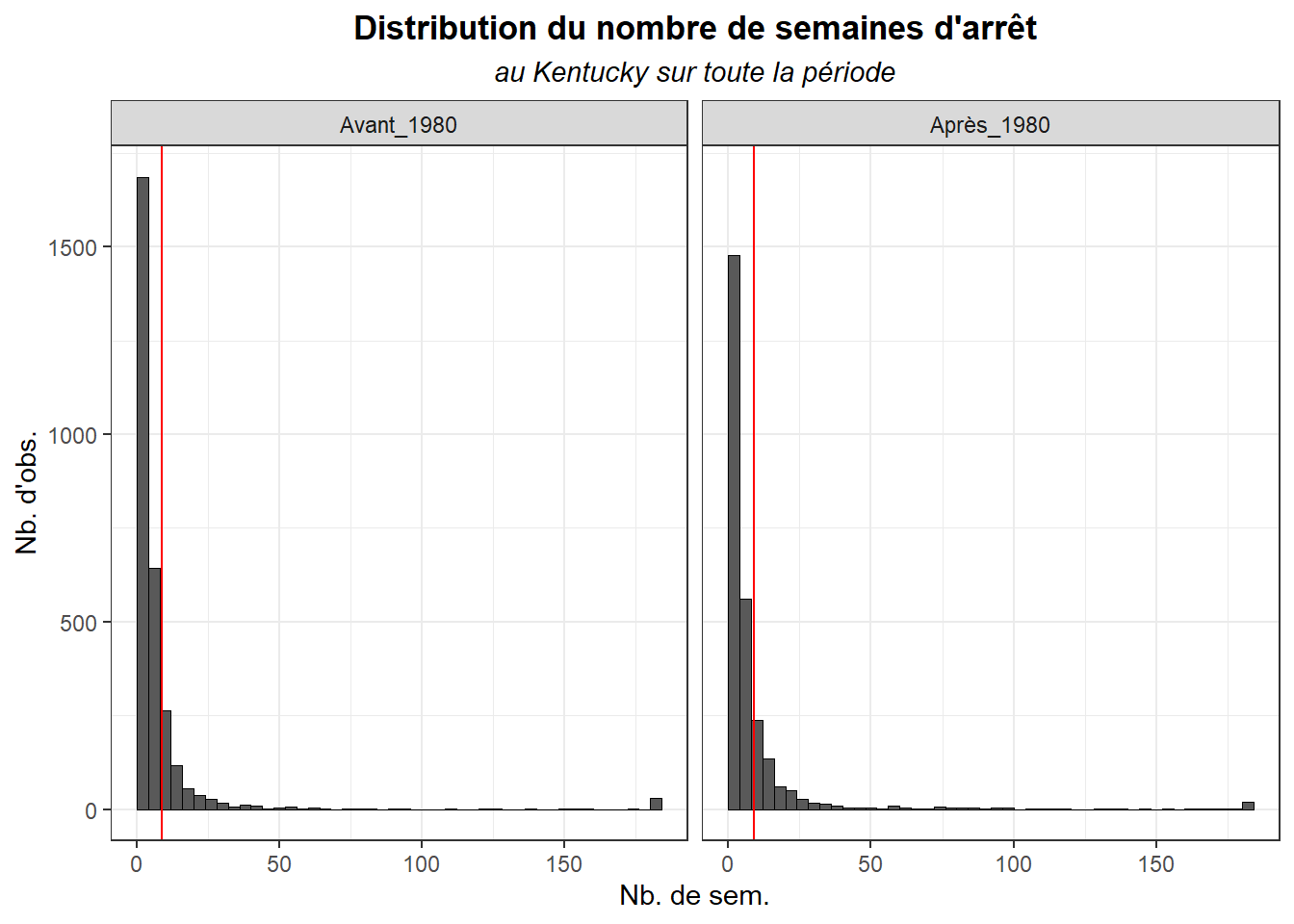
Dans tout les cas, on constate que les distributions sont très asymétriques mais également assez similaires.
Ici, travaillez à partir du log de la variable expliquée (log_duree) apparaît être une solution envisageable pour gérer les difficultés associées à l’asymétrie de sa distribution.
Examinons le changement au travers d’un histogramme. Adaptons l’échelle des abscisses pour que les valeurs apparaissent en nombre de semaines et non en log du nombre de semaines.
hist_var(dk$log_duree, dat= dk,biw=0.5,
tit="Distribution du log du nombre de semaines d'arrêt",
sub= "au Kentucky sur toute la période",
lx="Nb. de sem.",
ly="Nb. d'obs.")+
scale_x_continuous(labels=trans_format("exp",format=round))+
geom_vline(aes(xintercept = mean(log_duree)),
colour = 'red')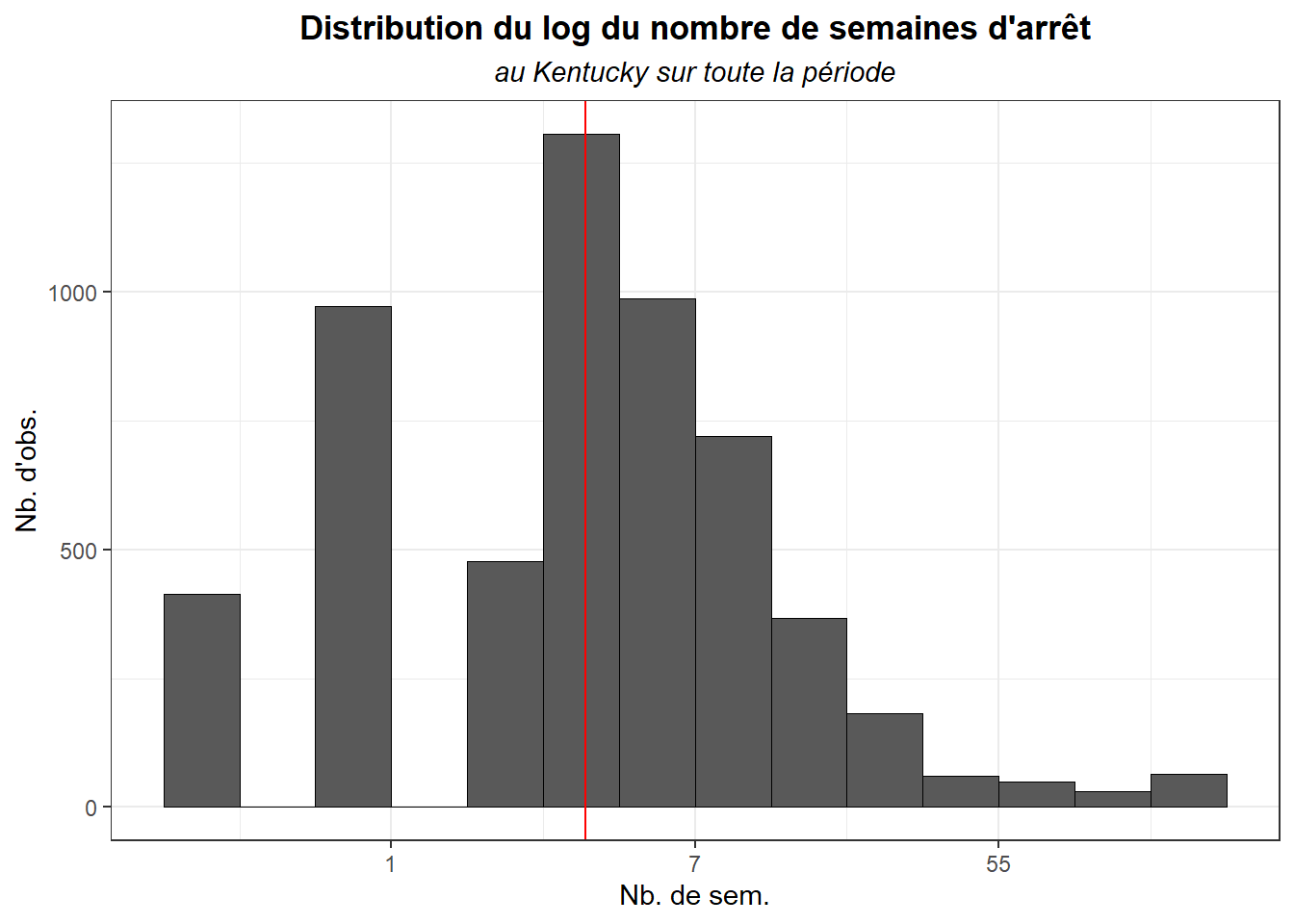
La distribution de log_duree est bien plus symétrique (proche d’une loi normale) ce qui n’est pas sans conséquences sur les tests statistiques mis en oeuvre.
dif_mean_t(log_duree,post,dat=dk)## Avant_1980 Après_1980 diff t p.value
## 1.233 1.326 0.093 -2.719 0.007Le test de différence de moyenne est ici toujours statistiquement significatif, mais cette fois au seuil de 1%. On trouve la même chose dans l’analyse de régression.
reg_naive2<-lm(log_duree~post,data = dk)
tidy(reg_naive2) %>%
mutate_if(is.numeric, round , digits=3)## # A tibble: 2 × 5
## term estimate std.error statistic p.value
## <chr> <dbl> <dbl> <dbl> <dbl>
## 1 (Intercept) 1.23 0.024 52.2 0
## 2 postAprès_1980 0.093 0.034 2.72 0.006Établissons les moyennes à partir des résultats de la régression.
data.frame(avant_1980=reg_naive2$coefficients[1],
après_1980=sum(reg_naive2$coefficients),
diffèrence=reg_naive2$coefficients[2]) %>%
round(digits = 3) %>% remove_rownames()## avant_1980 après_1980 diffèrence
## 1 1.233 1.326 0.093Visualisons les choses via les histogrammes.
hist_var(dk$log_duree, dat= dk,biw=0.5,
tit="Distribution du log du nombre de semaines d'arrêt",
sub= "au Kentucky sur toute la période",
lx="Nb. de sem.",
ly="Nb. d'obs.")+
facet_grid(.~post)+
scale_x_continuous(labels=trans_format("exp",format=round))+
geom_vline(aes(xintercept = mean(log_duree), group = post),
colour = 'red')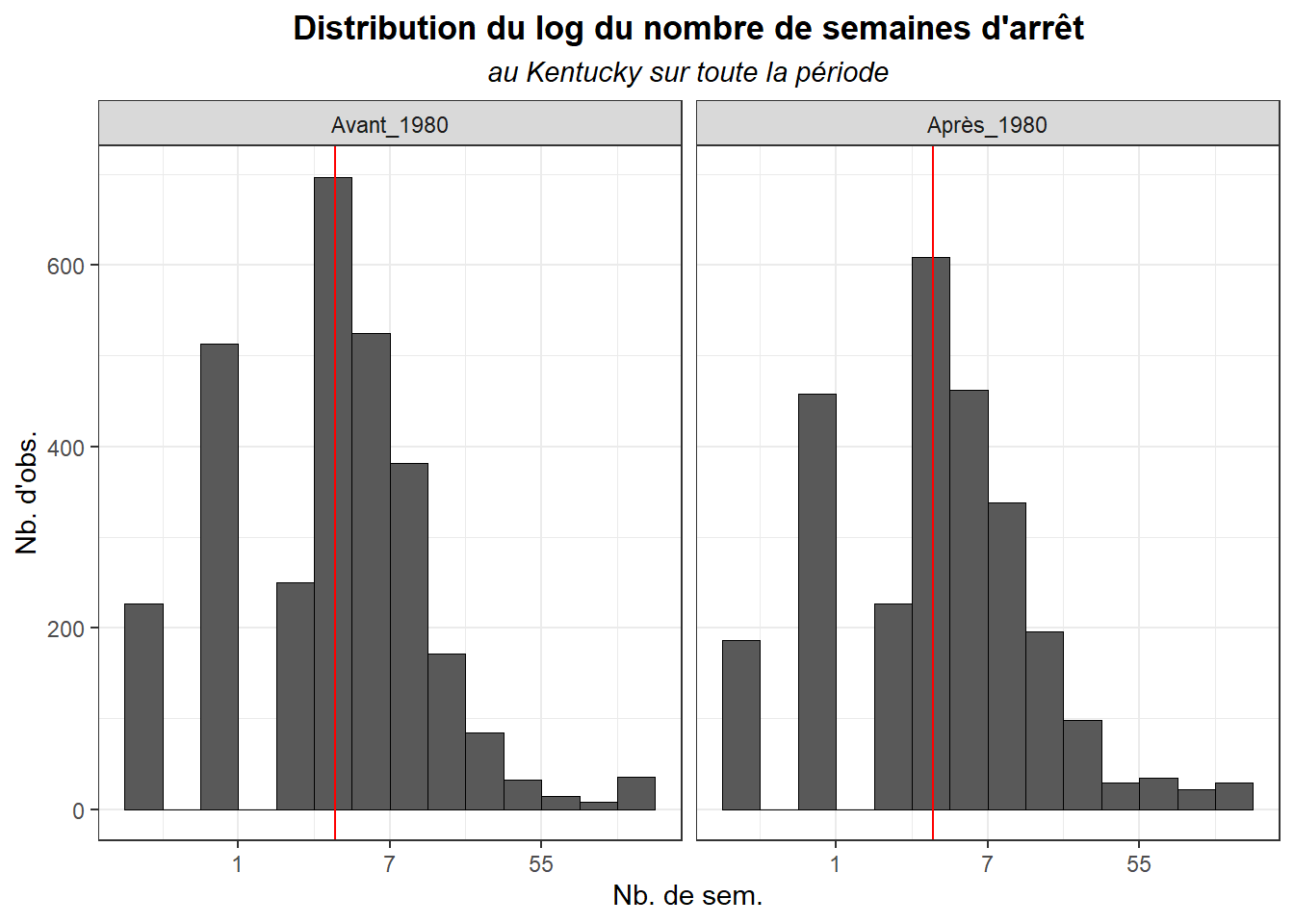
Graphe des moyennes et intervalles
Une autre façon d’illustrer l’existence de distributions de valeurs différentes entre les groupes d’observations avant et après le traitement, consiste à indiquer les valeurs moyennes à l’aide de points et d’agrémenter ces points de un segment représentant l’intervalle de confiance retenu. Prenons ici 95%. On a alors:
ggplot(data=dk,aes(x=post,y=log_duree))+
stat_summary(geom='pointrange',fun.data="mean_se",
fun.args = list(mult=qnorm(0.975)))+
labs(title="Moyennes et intervalle de confiance à 95%",
y="Nb de semaines")+
scale_y_continuous(labels=trans_format("exp",format = round(1)))+
theme_bw()+
theme(
plot.title = element_text(hjust=0.5,face='bold'),
axis.title.x = element_blank()
)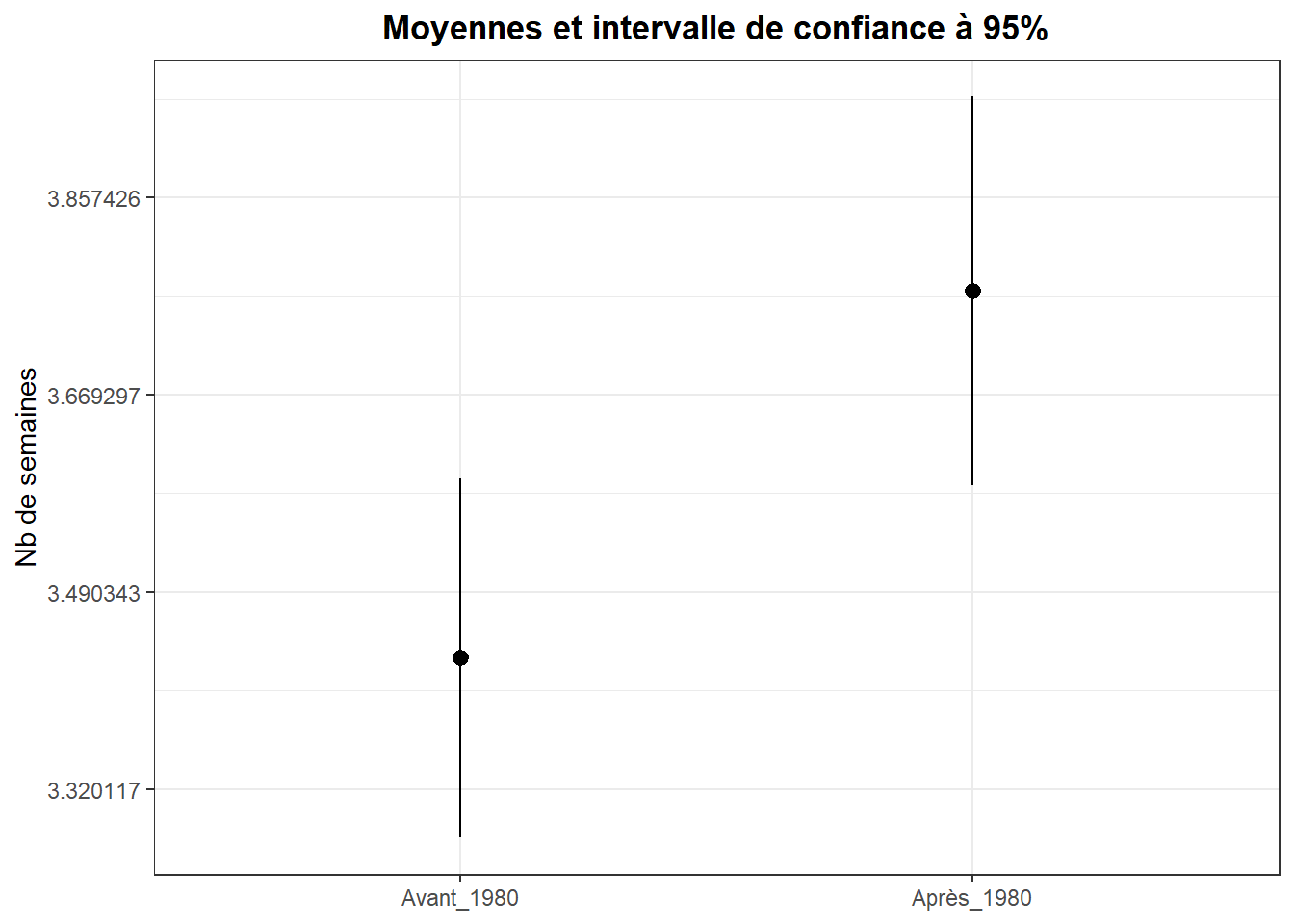
On voit plus nettement les différences avant/après qu’avec les histogrammes. Les intervalles de confiance se chevauchent très peu.
On peut également utiliser un strip chart. A la différence de la présentation des intervalles de confiance, cette représentation intègre l’ensemble des observations. Chaque point représente une observations.
ggplot(data=dk,aes(x=post,y=log_duree,colour=post))+
geom_point(alpha=0.2,size=0.5)+
stat_summary(aes(group=post),
geom='point',fun="median",color='red')+
labs(title="Durée des arrêts de travail
avant et aprés la réforme",
y="Nb de semaines")+
scale_y_continuous(labels=trans_format("exp",format = round(1)))+
theme_bw()+
theme(
plot.title = element_text(hjust=0.5,face='bold'),
axis.title.x = element_blank(),
legend.position = "none"
)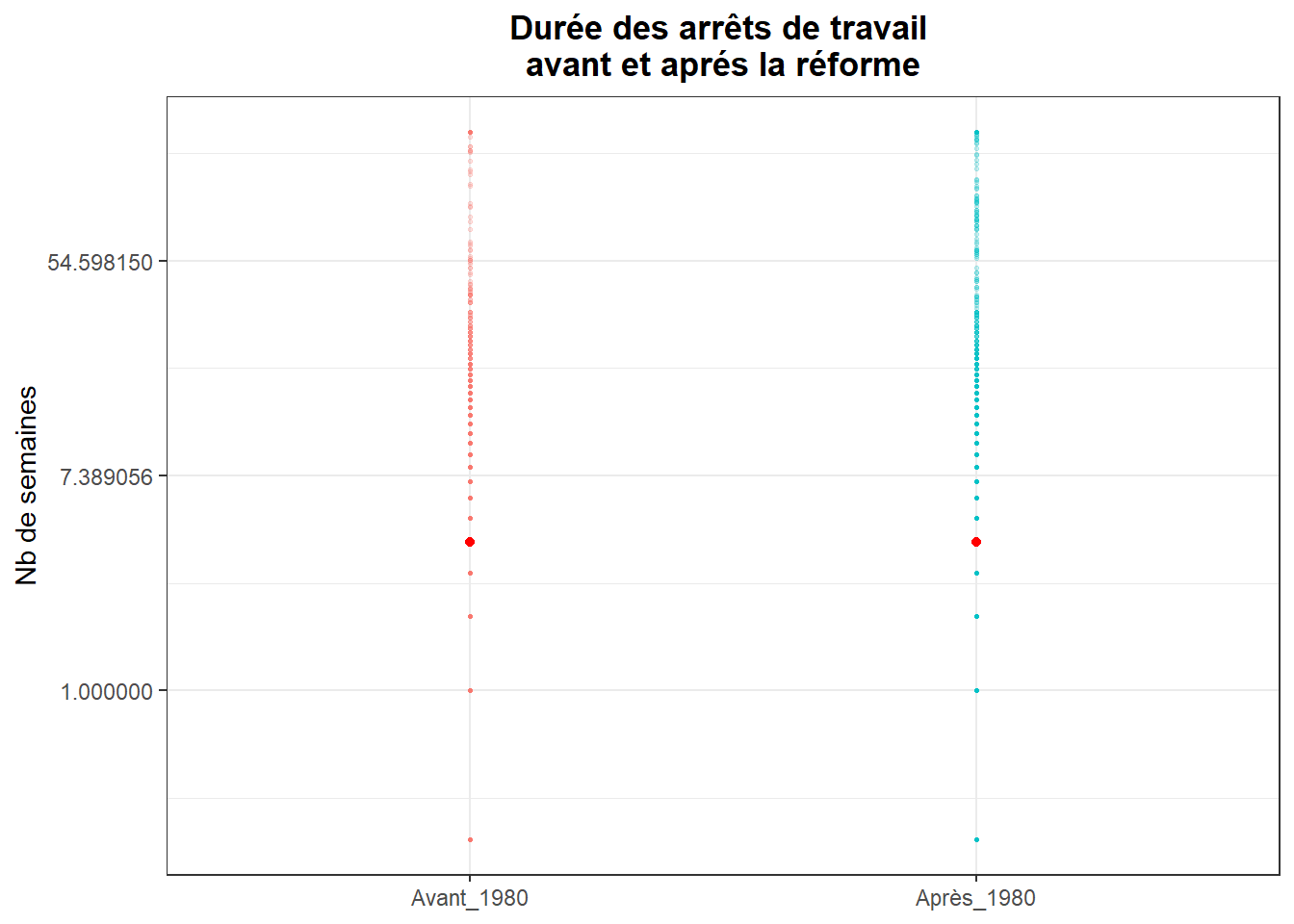
Cette représentation est peu claire, dans la mesure où il y a beaucoup de points qui se superposent. Pour y remédier, on peut utiliser le geom_jitter(), qui permet de positionner les points sur une base aléatoire selon une dimension (ici prenons la largeur).
ggplot(data=dk,aes(x=post,y=log_duree,colour=post))+
geom_jitter(alpha=0.5,size=0.5,width = 0.25)+
stat_summary(geom='point',fun="mean",color='red')+
labs(title="Durée des arrêts de travail
avant et aprés la réforme",
y="Nb de semaines")+
scale_y_continuous(labels=trans_format("exp",format = round(1)))+
theme_bw()+
theme(
plot.title = element_text(hjust=0.5,face='bold'),
axis.title.x = element_blank(),
legend.position='none'
)
Avant/après pour les traités
Peu importe, la manière de représenter les choses la différences entre la durée moyenne d’arrêt avant la réforme et après la réforme ne dit rien (ou pas grand chose) sur l’effet de celle-ci. En effet, la reforme n’affecte pas toute la population. Seuls les hauts revenus voient leur régime changer. Effectuons l’analyse sur ce sous-échantillon.
dif_mean_t(duree,post,dat=filter(dk,traite=="Haut_revenu"))## Avant_1980 Après_1980 diff t p.value
## 11.177 12.894 1.717 -1.468 0.142Pour la variable durée, la différence entre le nombre moyen de semaines d’arrêt avant et après la réforme n’est pas statistiquement significative.
Voyons les choses sur la base du logarithme de la durée.
dif_mean_t(log_duree,post, dat=filter(dk,traite=="Haut_revenu"))## Avant_1980 Après_1980 diff t p.value
## 1.382 1.580 0.198 -3.734 0.000Lorsque l’on passe par le log de la durée, la différence est clairement significative. On peut visualiser les choses à l’aide des intervalles de confiance.
ggplot(data=filter(dk,traite=="Haut_revenu"),
aes(x=post,y=log_duree))+
stat_summary(geom='pointrange',fun.data="mean_se",
fun.args = list(mult=1.96))+
labs(title="Durée des arrêts de travail
avant et aprés la réforme pour les hauts revenus",
subtitle = "Moyennes et intervalle de confiance à 95%",
y="Nb de semaines")+
scale_y_continuous(breaks=log(c(4.95,4.48,4.05,3.67)),
labels=c("4.95","4.48","4.05","3.67"))+
theme_bw()+
theme(
plot.title = element_text(hjust=0.5),
plot.subtitle = element_text(hjust=0.5),
axis.title.x = element_blank()
)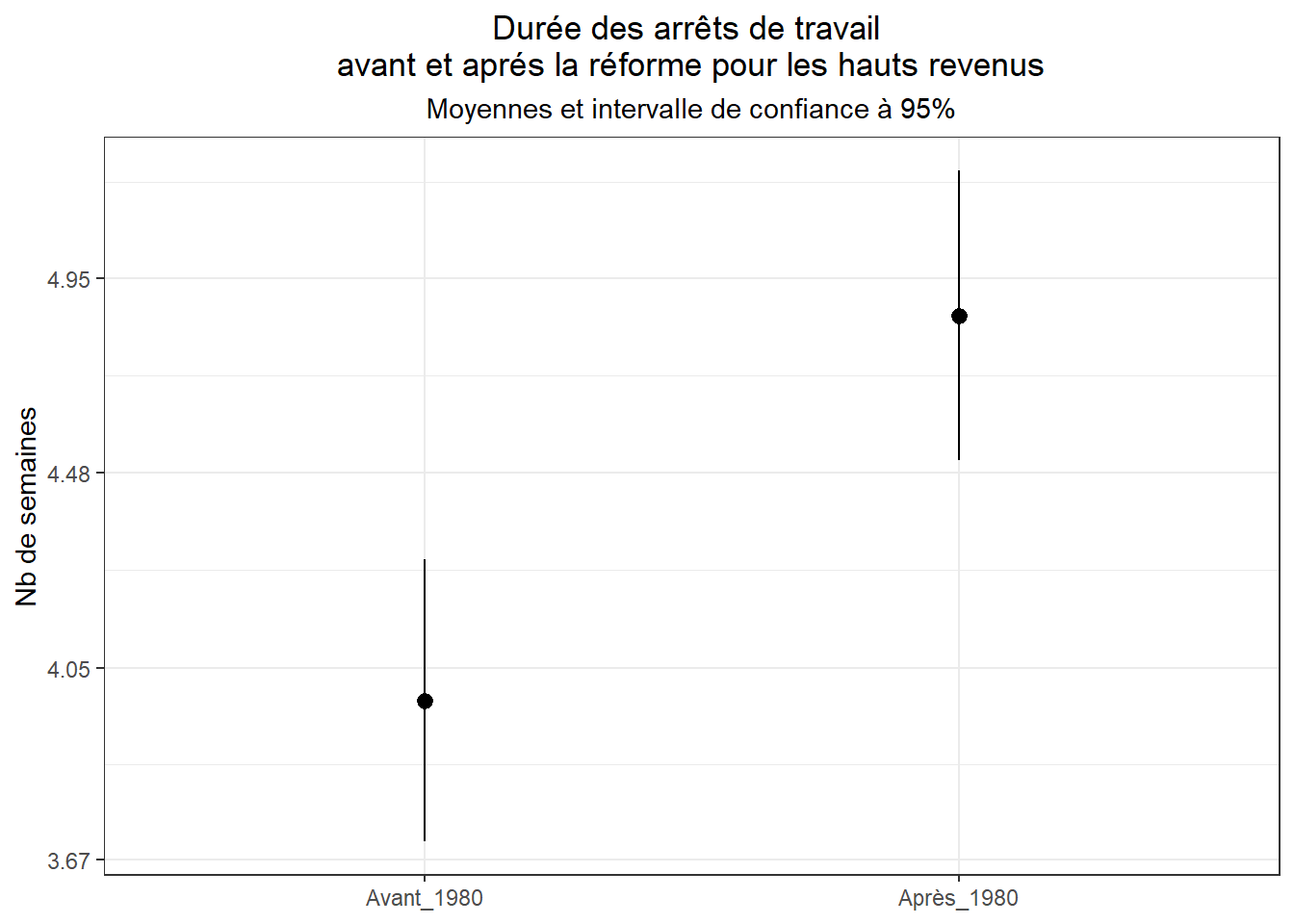
Ce résultat tendrait à accréditer l’hypothèse d’une augmentation de la durée d’arrêt de travail pour les traités (les hauts revenus) suite à la réforme. Cela va dans le sens d’un effet “positif” de la réforme. Néanmoins, cela peu cacher le fait qu’au moins en partie cette augmentation peut être due à une évolution générale non spécifique au traitement. Pour s’en donner une idée, on peut examiner l’évolution du groupe de contrôle (les bas revenus) suite à la réforme.
Avant/après pour le groupe de contrôle
Travaillons ici directement avec le log de la durée d’arrêt.
dif_mean_t(log_duree,post,dat=filter(dk,traite=="Bas_revenu"))## Avant_1980 Après_1980 diff t p.value
## 1.126 1.133 0.008 -0.174 0.862On voit que la différence entre les durées d’arrêt avant et après 1980 n’est pas statistiquement significative.
Visualisons les choses avec le graphe des intervalles de confiance.
ggplot(data=filter(dk,traite=="Bas_revenu"),
aes(x=post,y=log_duree))+
stat_summary(geom='pointrange',fun.data="mean_se",
fun.args = list(mult=1.96))+
labs(title="Durée des arrêts de travail
avant et aprés la réforme pour les Bas revenus",
subtitle = "Moyennes et intervalle de confiance à 95%",
y="Nb de semaines")+
scale_y_continuous(breaks=c(1.2,1.15,1.10),
labels=c("3.32","3.15","3.00"))+
theme_bw()+
theme(
plot.title = element_text(hjust=0.5),
plot.subtitle = element_text(hjust=0.5),
axis.title.x = element_blank()
)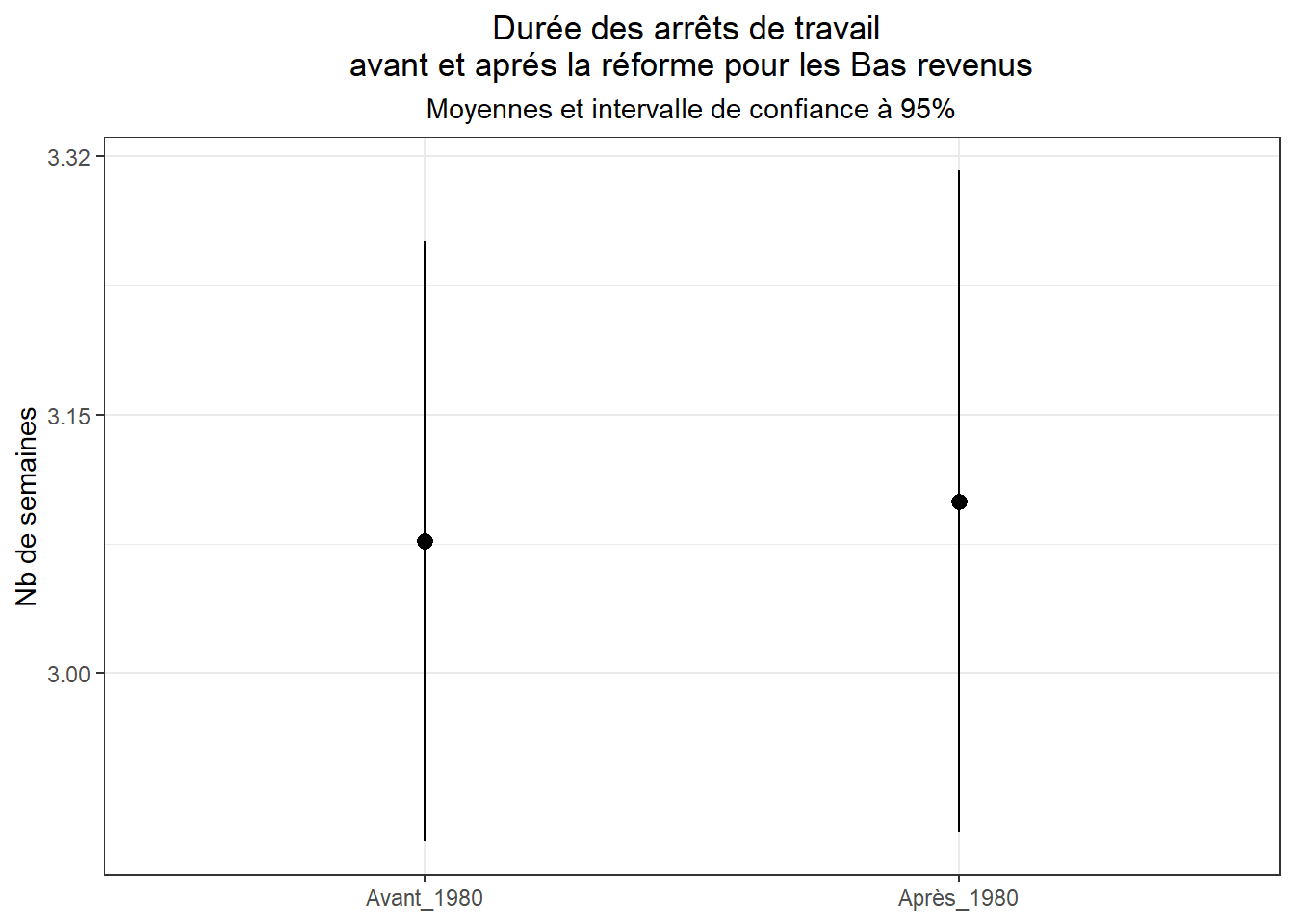
On voit bien que les intervalles des confiances se chevauchent. Il n’y a pas d’effet de la réforme sur le groupe de contrôle.
Il semble donc bien que la réforme ait un effet allant dans le sens d’une augmentation de la durée d’arrêt pour les traités (les hauts revenus) et pas sur le groupe de contrôle. Reste alors à mesurer cet effet.
Analyse Dif in Dif
Pour ce faire, il faut combiner les différences sur le groupe des traités et le groupe de contrôle. Commençons par les mettre en vis-à-vis.
rbind(bas_revenu=dif_mean_t(log_duree,post,
dat=filter(dk,traite=="Bas_revenu")),
haut_revenu=dif_mean_t(log_duree,post,
dat=filter(dk,traite=="Haut_revenu")))## Avant_1980 Après_1980 diff t p.value
## bas_revenu 1.126 1.133 0.008 -0.174 0.862
## haut_revenu 1.382 1.580 0.198 -3.734 0.000Pour déterminer l’effet du traitement, il suffit de soustraire à la différence avant et après traitement des traités (hauts revenus), la différence avant et après traitement du groupe de contrôle (bas revenus). Cet estimateur est appelé Difference in Difference (ou double différence en français). On a ici:
c(dif_in_dif=dif_mean_t(log_duree,post,
dat=filter(dk,traite=="Haut_revenu"))[3]-dif_mean_t(log_duree,post,
dat=filter(dk,traite=="Bas_revenu"))[3])## dif_in_dif.diff
## 0.19L’effet du traitement, estimé sur le log de la durée d’arrêt, est de 0,19 (log semaines, soit un peu plus d’une semaine aux arrondis prés).
Le tableau des différences
Résumons tout cela dans une tableau unique. Commençons par établir les moyennes de log_duree pour le groupe des traités et la groupe de contrôle pour les périodes avant et après le traitement.
moy<-cbind(rbind(Haut_revenu=
mean(filter(dk,traite=="Haut_revenu"&post=="Avant_1980")$log_duree),
Bas_revenu=
mean(filter(dk,traite=="Bas_revenu"&post=="Avant_1980")$log_duree)),
rbind(Haut_revenu=
mean(filter(dk,traite=="Haut_revenu"&post=="Après_1980")$log_duree),
Bas_revenu=
mean(filter(dk,traite=="Bas_revenu"&post=="Après_1980")$log_duree))) %>%
round(digits = 3)
colnames(moy)<-c("Avant 1980","Après 1980")
moy## Avant 1980 Après 1980
## Haut_revenu 1.382 1.580
## Bas_revenu 1.126 1.133Ceci fait, on peut déterminer les différences. Commençons par celles que nous avons déjà calculées (avant/après) et ajoutons les différences traité/contrôle.
diff_h<-moy[,2]-moy[,1]
diff_v<-c(moy[1,]-moy[2,],NA)
moy_h<-cbind(moy,diff_h)
moy_hv<-rbind(moy_h,diff_v)
moy_hv## Avant 1980 Après 1980 diff_h
## Haut_revenu 1.382 1.580 0.198
## Bas_revenu 1.126 1.133 0.007
## diff_v 0.256 0.447 NAOn peut retrouver notre diff in diff soit en prenant les différences verticales [(traitéav-controleav )-(traitéap-controleap)] soit en prenant les différences horizontales [(traitéap-traitéav )-(controleap-controleav)] . On trouve le même effet pour le traitement à 0,191.
did<-moy_hv[3,2]-moy_hv[3,1]
did## [1] 0.191did<-moy_hv[1,3]-moy_hv[2,3]
did## [1] 0.191Ajoutons la double différence à notre table pour la compléter.
moy_hv[3,3]<-did
moy_hv## Avant 1980 Après 1980 diff_h
## Haut_revenu 1.382 1.580 0.198
## Bas_revenu 1.126 1.133 0.007
## diff_v 0.256 0.447 0.191Représentation graphique
L’ensemble peut également être présenté graphiquement au travers des intervalles de confiance. Commençons par réunir nos graphes précédents en utilisant les facets.
ggplot(dk, aes(x = traite, y = log_duree)) +
stat_summary(geom = "pointrange", size = 1,
color = "red",
fun.data = "mean_se",
fun.args = list(mult = 1.96)) +
labs(title="Durée des arrêts de travail",
subtitle = "Moyennes et intervalle de confiance à 95%",
y="Nb de semaines")+
scale_y_continuous(breaks=c(1.6,1.4,1.2),
labels=c("4.95","4.05","3.32"))+
facet_wrap(~ post)+
theme_bw()+
theme(
plot.title = element_text(hjust=0.5),
plot.subtitle = element_text(hjust=0.5),
axis.title.x = element_blank()
)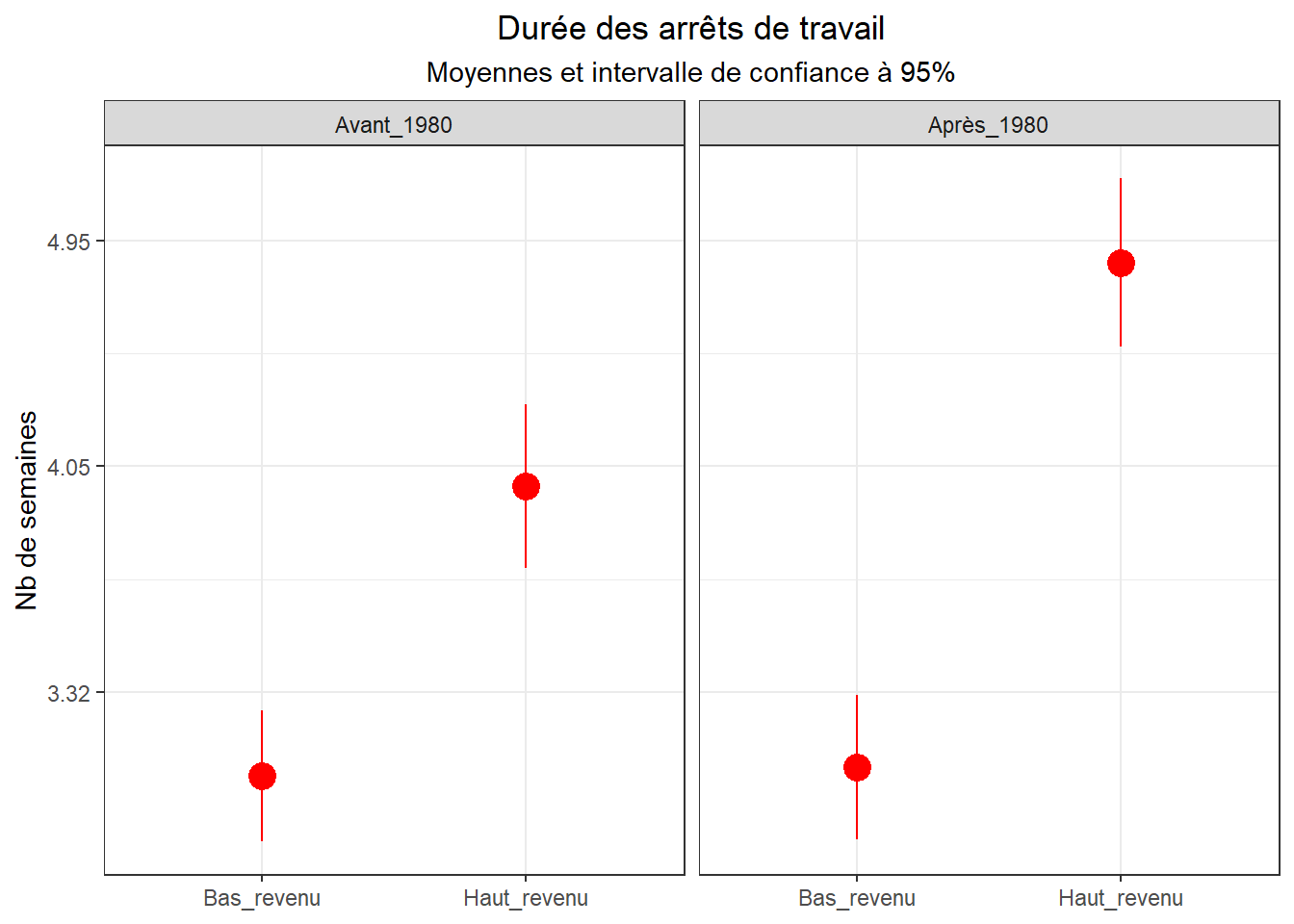
On peut aussi tout mettre sur une seule figure (sans passer par les facets). Elle inclut des segments pour marquer l’évolution de la variable expliquée dans le temps (avant/après le traitement). Mais pour ce faire, créons au préalable une base avec les moyennes.
bas_g<-dk %>%
group_by(traite,post) %>%
summarise(log_duree_m=mean(log_duree))
bas_g## # A tibble: 4 × 3
## # Groups: traite [2]
## traite post log_duree_m
## <fct> <fct> <dbl>
## 1 Bas_revenu Avant_1980 1.13
## 2 Bas_revenu Après_1980 1.13
## 3 Haut_revenu Avant_1980 1.38
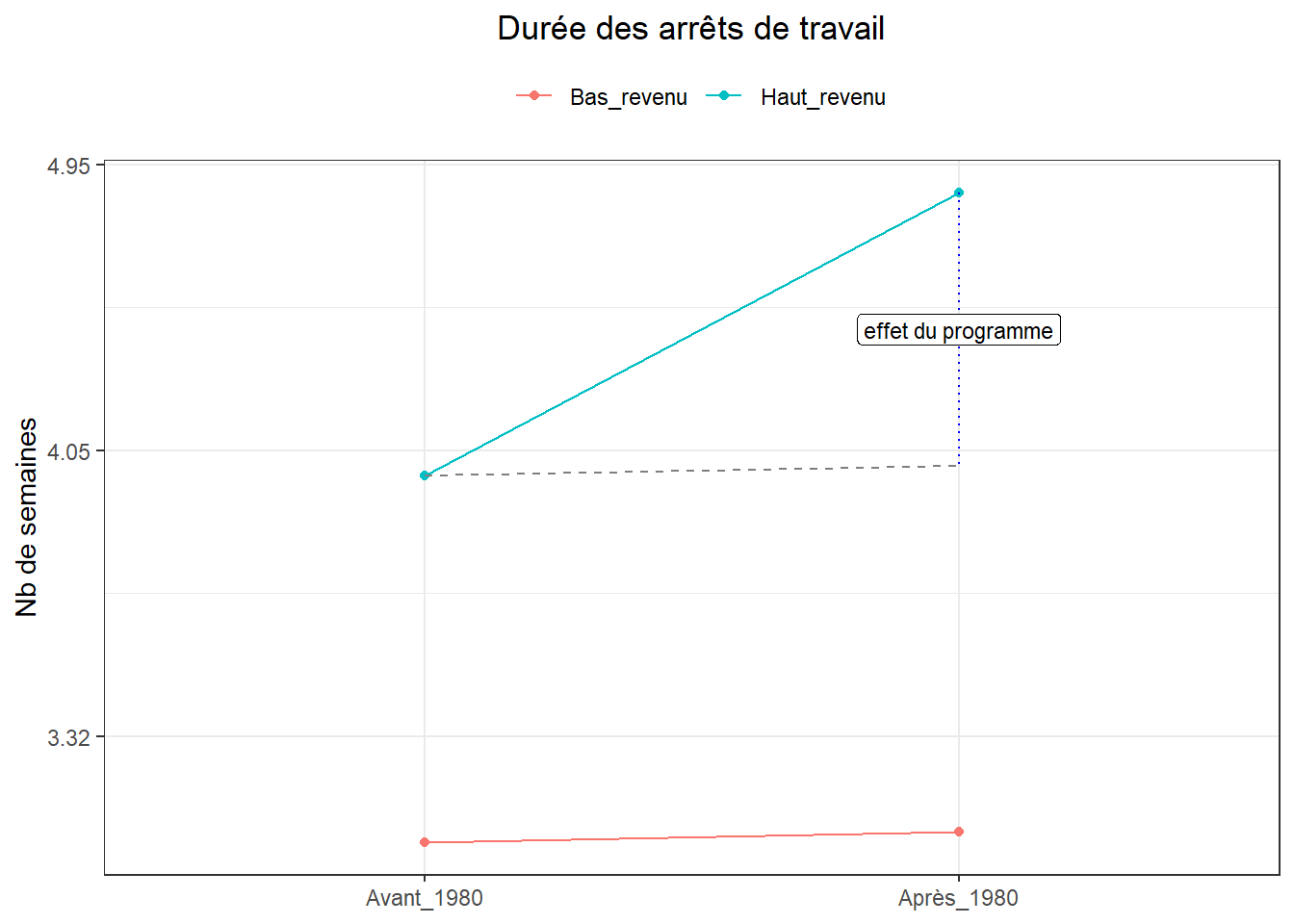
## 4 Haut_revenu Après_1980 1.58Une fois ces valeurs établies, marquons-les par un jeu de points et de lignes. Le contre-factuel, ce qui ce serait passé pour les traités s’il n’avait pas été traité, est figuré en pointillés.
ggplot(bas_g, aes(x = post,
y = log_duree_m,
color = traite)) +
geom_point() +
geom_line(aes(group = traite)) +
labs(title="Durée des arrêts de travail",
y="Nb de semaines",
color="")+
scale_y_continuous(breaks=c(1.6,1.4,1.2),
labels=c("4.95","4.05","3.32"))+
annotate(geom = "segment", x = "Avant_1980",
xend = "Après_1980",
y = bas_g$log_duree_m[3],
yend = bas_g$log_duree_m[4] - did,
linetype = "dashed", color = "grey50") +
annotate(geom = "segment", x = "Après_1980",
xend = "Après_1980",
y = bas_g$log_duree_m[4] ,
yend = bas_g$log_duree_m[4] - did,
linetype = "dotted", color = "blue") +
annotate(geom = "label", x = "Après_1980",
y = bas_g$log_duree_m[4] - (did / 2),
label = "effet du programme", size = 3)+
theme_bw()+
theme(
plot.title = element_text(hjust=0.5),
axis.title.x = element_blank(),
legend.position = "top"
)
Analyse de régression
Le calcul de la statistique de double différence au travers d’éléments de statistiques descriptives présente le défaut de ne pas fournir (directement) de test statistique sur sa valeur. On ne peut pas dire si l’effet du traitement est statistiquement différent de zéro. Pour y remédier, on préférera utiliser une estimation basée sur une régression. Celle-ci fournit la même valeur, mais, cette fois, elle est accompagnée d’un écart-type (et a fortiori une erreur standard) permettant la construction d’un test (généralement de Student contre la valeur 0 - H0 Le traitement n’a pas d’effet).
Cette régression est construite à partir de l’interaction des termes désignant le groupe des traités (traite) et la période pré et post traitement (post).
model_small <- lm(log_duree ~ traite + post + traite * post,
data = dk)
tidy(model_small) %>%
mutate_if(is.numeric, round , digits=3)## # A tibble: 4 × 5
## term estimate std.error statistic p.value
## <chr> <dbl> <dbl> <dbl> <dbl>
## 1 (Intercept) 1.13 0.031 36.6 0
## 2 traiteHaut_revenu 0.256 0.047 5.41 0
## 3 postAprès_1980 0.008 0.045 0.171 0.864
## 4 traiteHaut_revenu:postAprès_1980 0.191 0.069 2.78 0.005L’avantage d’utiliser un régression pour réaliser l’analyse Diff-in-Diff repose sur le fait de pouvoir intégrer des variables de contrôle. Révisons la base de données pour en intégrer (sexe, age, hospitalisation ou non, secteur d’activité, type de blessure, salaire avant la blessure).
kentucky_fixed <- dat %>%
filter(ky==1) %>%
mutate(indust = as.factor(indust),
injtype = as.factor(injtype),
traite=factor(highearn,labels=c("Bas_revenu","Haut_revenu")),
post=factor(afchnge,labels=c("Avant_1980","Après_1980")))Réalisons la régression en incluant les variables de contrôle.
model_big <- lm(ldurat~traite + post + traite * post +
male + married + age + hosp + indust + injtype + lprewage,
data = kentucky_fixed)
tidy(model_big) %>%
mutate_if(is.numeric, round , digits=3)## # A tibble: 18 × 5
## term estimate std.error statistic p.value
## <chr> <dbl> <dbl> <dbl> <dbl>
## 1 (Intercept) -1.53 0.422 -3.62 0
## 2 traiteHaut_revenu -0.152 0.089 -1.70 0.089
## 3 postAprès_1980 0.05 0.041 1.20 0.231
## 4 male -0.084 0.042 -1.99 0.046
## 5 married 0.057 0.037 1.52 0.129
## 6 age 0.007 0.001 4.86 0
## 7 hosp 1.13 0.037 30.5 0
## 8 indust2 0.184 0.054 3.40 0.001
## 9 indust3 0.163 0.038 4.32 0
## 10 injtype2 0.935 0.144 6.51 0
## 11 injtype3 0.635 0.085 7.44 0
## 12 injtype4 0.555 0.093 5.97 0
## 13 injtype5 0.641 0.085 7.50 0
## 14 injtype6 0.615 0.086 7.13 0
## 15 injtype7 0.991 0.191 5.20 0
## 16 injtype8 0.434 0.119 3.65 0
## 17 lprewage 0.284 0.08 3.55 0
## 18 traiteHaut_revenu:postAprès_1980 0.169 0.064 2.64 0.008Le coefficient associé à la double différence est ici renvoyé à la fin du tableau (la ligne 18). Isolons la ligne correspondante.
tidy(model_big)[18,] %>%
mutate_if(is.numeric, round , digits=3)## # A tibble: 1 × 5
## term estimate std.error statistic p.value
## <chr> <dbl> <dbl> <dbl> <dbl>
## 1 traiteHaut_revenu:postAprès_1980 0.169 0.064 2.64 0.008La double différence est de 0,169. Le coefficient a légèrement diminué par rapport à l’analyse sans variable de contrôle. Néanmoins, l’effet du traitement reste légèrement au dessus d’une semaine en plus en moyenne.
Il serait intéressant de présenter ces analyses dans un même tableau. Utilisons le package huxtable.
library(huxtable)
huxreg(model_small, model_big)| (1) | (2) | |
|---|---|---|
| (Intercept) | 1.126 *** | -1.528 *** |
| (0.031) | (0.422) | |
| traiteHaut_revenu | 0.256 *** | -0.152 |
| (0.047) | (0.089) | |
| postAprès_1980 | 0.008 | 0.050 |
| (0.045) | (0.041) | |
| traiteHaut_revenu:postAprès_1980 | 0.191 ** | 0.169 ** |
| (0.069) | (0.064) | |
| male | -0.084 * | |
| (0.042) | ||
| married | 0.057 | |
| (0.037) | ||
| age | 0.007 *** | |
| (0.001) | ||
| hosp | 1.130 *** | |
| (0.037) | ||
| indust2 | 0.184 *** | |
| (0.054) | ||
| indust3 | 0.163 *** | |
| (0.038) | ||
| injtype2 | 0.935 *** | |
| (0.144) | ||
| injtype3 | 0.635 *** | |
| (0.085) | ||
| injtype4 | 0.555 *** | |
| (0.093) | ||
| injtype5 | 0.641 *** | |
| (0.085) | ||
| injtype6 | 0.615 *** | |
| (0.086) | ||
| injtype7 | 0.991 *** | |
| (0.191) | ||
| injtype8 | 0.434 *** | |
| (0.119) | ||
| lprewage | 0.284 *** | |
| (0.080) | ||
| N | 5626 | 5347 |
| R2 | 0.021 | 0.190 |
| logLik | -9321.997 | -8323.388 |
| AIC | 18653.994 | 16684.775 |
| *** p < 0.001; ** p < 0.01; * p < 0.05. | ||
Nous aurions pu prolonger l’exemple en abordant les two-way fixed effect qui sont une autre manière d’estimer le coefficient associé à la double différence. Néanmoins la base prise pour exemple ne le permet pas. Il n’y a pas d’identifiant individuel permettant d’attribuer des effets fixes individuels. Nous renvoyons donc cela à un prochain post.