Venons-en à notre second post de la sous-série de GT consacrée à l’illustration distribution des variables quantitatives. Il s’agit ici de traiter des histogrammes en pyramide. Ceux-ci permettent de faciliter la comparaison de la distribution d’une variable entre deux groupes d’observations. Ils sont souvent mobilisés en démographie pour mettre en regard les effectifs des différences classes d’âge pour chaque sexe (pour une zone géographique et à une date donnée). Le principe du graphe est simple. On a un histogramme réalisé sur la même variable avec les mêmes intervalles pour les deux groupes qui sont présentés à l’horizontale et orientés en miroir. Cela permet à la fois de mettre en évidence les similarités au travers les symétries et les différences au travers les dissymétries. Son principal défaut repose dans le fait que les comparaisons qu’il permet se limitent à deux groupes. Nous verrons par la suite d’autres graphes ouvrant plus de possibilité.
Pour illustrer la construction de l’histogramme en pyramide, restons dans les applications financières. Depuis le début des années 80, différentes études se sont attaché à identifier des anomalies affectant les rendements des actions au regard de ce que postule la théorie de l’efficience des marchés. Il s’agit pour elles de mettre en évidence des régularités dans les rendements notamment sur une base calendaire peu compatible avec l’efficience et son pendant d’absence de toute forme saisonnalité dans les cours. Une des premières concerne ce que l’on nomme l’effet weekend mise en évidence notamment par French (1980) sur les marchés US. Il relève que sur la période 1953-1977 des rendements en moyenne moins important les lundi et plus important les vendredi sur l’indice Standard and Poor. D’autres anomalies calendaires, on était mises en évidence comme l’effet fin de mois, l’effet vacances… Elles ont pour la plupart d’entre elles ont disparu.
Nous reviendrons ici sur l’effet weekend. Mais, comme toujours avant d’aller plus loin, chargeons les packages que nous mobiliserons par la suite, le tidyverse, scales, GT, pour la mise en forme de tableaux, patchwork, pour assembler des graphes, et, pour les données, tidyquant.
library(tidyverse)
library(scales)
library(gt)
library(patchwork)
library(tidyquant)Ceci fait attachons nous à charger les données à partir de la fonction tq_get(). Indiquons le ticker de l’indice Standard & Poor 500 “^GSPC” et la période retenue qui est ici large allant de 1954 à 2023. Visualisons le résultat via glimpse().
dat<-tq_get("^GSPC",from="1954-01-31", to = "2023-05-04")
glimpse(dat)## Rows: 17,434
## Columns: 8
## $ symbol <chr> "^GSPC", "^GSPC", "^GSPC", "^GSPC", "^GSPC", "^GSPC", "^GSPC"…
## $ date <date> 1954-02-01, 1954-02-02, 1954-02-03, 1954-02-04, 1954-02-05, …
## $ open <dbl> 25.99, 25.92, 26.01, 26.20, 26.30, 26.23, 26.17, 26.14, 26.06…
## $ high <dbl> 25.99, 25.92, 26.01, 26.20, 26.30, 26.23, 26.17, 26.14, 26.06…
## $ low <dbl> 25.99, 25.92, 26.01, 26.20, 26.30, 26.23, 26.17, 26.14, 26.06…
## $ close <dbl> 25.99, 25.92, 26.01, 26.20, 26.30, 26.23, 26.17, 26.14, 26.06…
## $ volume <dbl> 1740000, 1420000, 1690000, 2040000, 2030000, 2180000, 1880000…
## $ adjusted <dbl> 25.99, 25.92, 26.01, 26.20, 26.30, 26.23, 26.17, 26.14, 26.06…Continuons en réduisant les données aux seules nécessaires (la date et le cours ajusté) et calculons les rendements de l’indice de manière discrète et continue.
dat<-dat %>% select(date,adjusted) %>%
mutate(ret=adjusted/lag(adjusted)-1,
ret_c=log(adjusted/lag(adjusted))) %>%
drop_na()Travaillons maintenant sur les dates. Isolons le jours de la semaine grace à wday(). Le premier jour de la semaine ici est le dimanche. Il est marqué de la valeur 1. Les lundi et vendredi sont ainsi marqués des valeurs 2 et 6. Codons une variable les mettons en évidence. Pour ce faire, utilisons case_when().
dat<-dat%>% mutate(day_of_the_week=wday(date),
day_lab=wday(date,label=TRUE),
jour=case_when(wday(date)==2~"Monday",
wday(date)==6~"Friday",
.default = "Other_day")) %>%
select(date,jour,ret,ret_c)Établissons quelques statistiques descriptives avant d’aller plus loin. Faisons le tout d’abord pour l’ensemble de la base.
dat %>% group_by(jour) %>%
summarise(moyenne=round(mean(ret)*100,digits=2),
ecart_type=round(sd(ret)*100,digits=2),
n=n())## # A tibble: 3 × 4
## jour moyenne ecart_type n
## <chr> <dbl> <dbl> <int>
## 1 Friday 0.06 0.93 3482
## 2 Monday -0.05 1.16 3332
## 3 Other_day 0.05 0.98 10619Voyons-le également pour la période étudiée par French (1953-1977).
dat %>% filter(date>date("1953/01/01")&
date<date("1977/12/31")) %>%
group_by(jour) %>%
summarise(moyenne=round(mean(ret)*100,digits=2),
ecart_type=round(sd(ret)*100,digits=2),
n=n())## # A tibble: 3 × 4
## jour moyenne ecart_type n
## <chr> <dbl> <dbl> <int>
## 1 Friday 0.11 0.67 1199
## 2 Monday -0.15 0.86 1170
## 3 Other_day 0.05 0.74 3632On constate que les rendements des lundi sont bien en moyennes inférieures à ceux des autres jours et ceux des vendredi supérieures. Néanmoins, les écart-types sont relativement importants, les différences ne sont peut être pas statistiquement significatives. Le même type de différences est constatées sur l’échantillon inspiré de French mais avec des moyennes plus contrastées et des écart-types plus petits. Créons une fonction pour faciliter les choses l’enchaînement des tests de différences de moyenne (avec t.test()).
test_jour<-function(data,jour_exclu){
d<-filter(data,jour!=jour_exclu)
t_stat<-t.test(data=d,ret~jour)$statistic
p_val<-t.test(data=d,ret~jour)$p.value
vect<-round(c(t_stat,p_val),digits=3)
names(vect)<-c("t","p_value")
return(vect)
}Assemblons un tableau reprenant l’ensemble. Amusons-nous un peu avec GT pour le mettre en forme. Ajoutons un test sur la période post 2000 afin de voir si les anomalies éventuelles persistent.
full<-cbind(Lundi=test_jour(data=dat,
jour_exclu = "Friday"),
Vendredi=test_jour(data=dat,
jour_exclu = "Monday"))
french<-cbind(Lundi=
test_jour(data=filter(dat,
date>date("1953/01/01")&
date<date("1977/12/31")),
jour_exclu = "Friday"),
Vendredi=test_jour(data=filter(dat,
date>date("1953/01/01")&
date<date("1977/12/31")),
jour_exclu = "Monday"))
deux_milles<-cbind(Lundi=
test_jour(data=filter(dat,
date>date("2000/01/01")),
jour_exclu = "Friday"),
Vendredi=test_jour(data=filter(dat,
date>date("2000/01/01")),
jour_exclu = "Monday"))
data.frame(full,french,deux_milles) %>%
gt(rownames_to_stub = TRUE) %>%
tab_spanner(
label = "Full",
columns = c(Lundi, Vendredi)) %>%
tab_spanner(
label = "French (1953-1977)",
columns = c(Lundi.1, Vendredi.1)) %>%
tab_spanner(
label = "Aprés 2000",
columns = c(Lundi.2, Vendredi.2)) %>%
cols_label(
Lundi.1 = "Lundi",
Vendredi.1 = "Vendredi",
Lundi.2 = "Lundi",
Vendredi.2 = "Vendredi") %>%
data_color(
rows = "p_value",
direction = "row",
method = "quantile",
quantiles = 2,
palette = c("blue", "white"))|
Full
|
French (1953-1977)
|
Aprés 2000
|
||||
|---|---|---|---|---|---|---|
| Lundi | Vendredi | Lundi | Vendredi | Lundi | Vendredi | |
| t | -4.711 | 0.468 | -7.149 | 2.375 | -0.994 | -1.148 |
| p_value | 0.000 | 0.640 | 0.000 | 0.018 | 0.320 | 0.251 |
On constate que les différences sont biens significatives pour les deux jours sur la période étudiée par French, mais seulement significative sur l’ensemble de la période pour le lundi et que passé 2000 plus rien n’est significatif. L’anomalie n’existe plus sur le Standard & Poor 500. Il serait donc vain de compter dessus pour faire fortune… Mais revenons-en à nos histogrammes.
Le premier réflexe que l’on pourrait avoir pour illustrer l’ensemble serait de travailler à partir de facets positionnant les rendements des différents jours les uns après les autres. Limitons nous pour l’instant à l’échantillon total. On aurait alors quelque choses de ce type (avec un peu de mise en forme). Nous utilisons ici 52 intervalles en application de la règle de Rule.
ggplot(data=dat,aes(x=ret,fill=jour))+
geom_histogram(aes(y=after_stat(density)),
bins=52,color='black')+
labs(title="Histogrammes des rendements
journaliers du S&P500",
caption="Source: données Yahoo! Finance")+
scale_x_continuous(labels=label_percent(accuracy = 1))+
scale_y_continuous(labels=label_percent(scale=1))+
facet_grid(rows=vars(jour))+
theme_minimal()+
theme(
plot.title = element_text(hjust = 0.5,face='bold'),
plot.caption = element_text(hjust = 1,face='italic'),
axis.title = element_blank(),
legend.position = "none")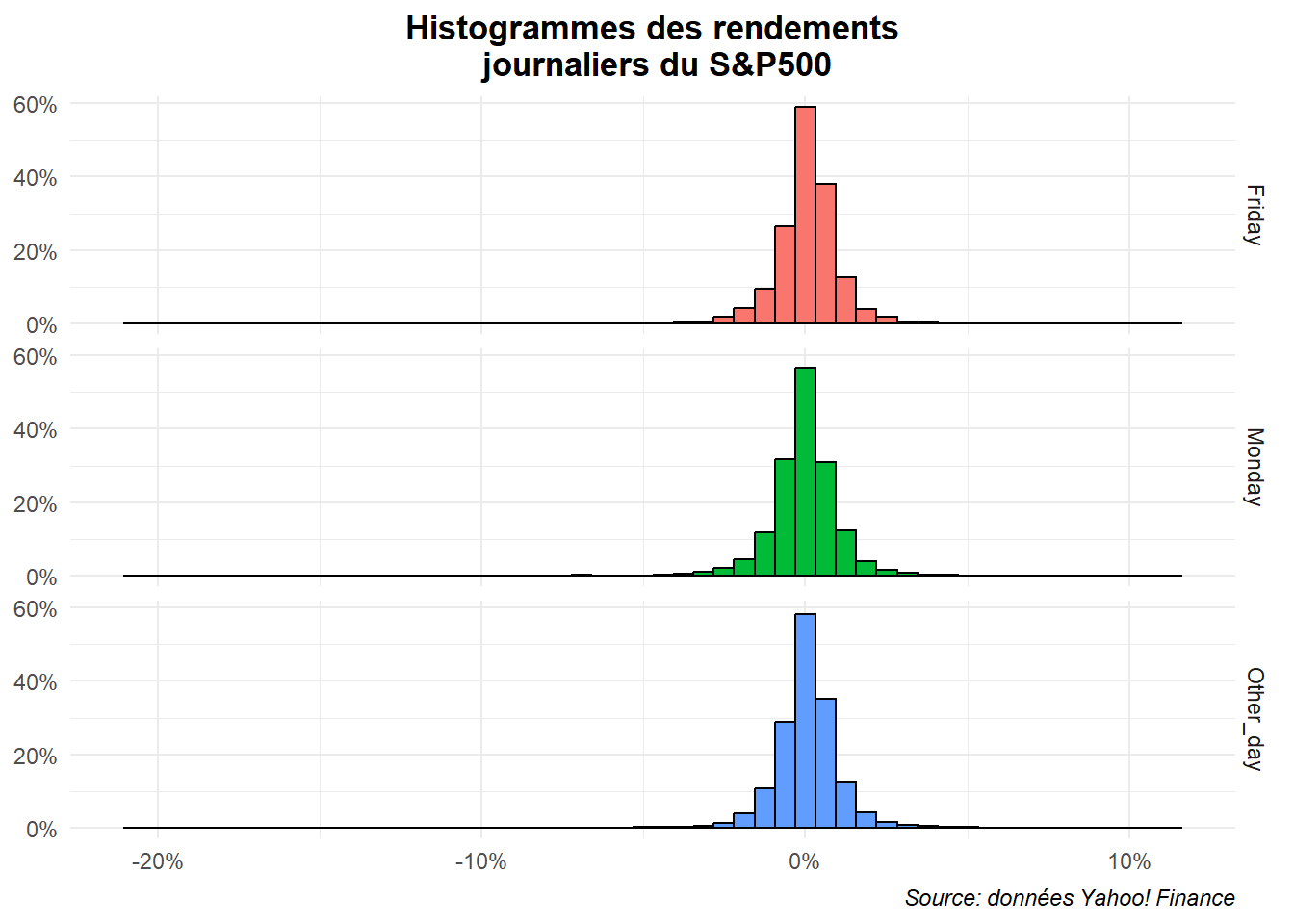
L’ensemble est assez satisfaisant mais il serait peut-être plus lisible si on exclut de la visualisation les valeurs extrêmes. Winsorisons la série et profitons en pour marquer la moyenne.
dat_moy<-dat %>%
group_by(jour) %>%
summarise(moy_ret=mean(ret))
ggplot(data= filter(dat,
ret>=quantile(ret,probs=.01)&
ret<quantile(ret,probs=.99)),
aes(x=ret,fill=jour))+
geom_histogram(aes(y=after_stat(density)),
bins=52,color='black')+
geom_vline(data=dat_moy,aes(xintercept = moy_ret),color='red')+
labs(title="Histogrammes des rendements journaliers du S&P500",
subtitle = "(moyenne en rouge - graphe sans les premiers et derniers percentiles)",
caption="Source: données Yahoo! Finance")+
scale_x_continuous(labels=label_percent(accuracy = 1))+
scale_y_continuous(labels=label_percent(scale=1))+
facet_grid(rows=vars(jour))+
theme_minimal()+
theme(
plot.title = element_text(hjust = 0.5,face='bold'),
plot.subtitle = element_text(hjust = 0.5,face='italic',size=8),
plot.caption = element_text(hjust = 1,face='italic'),
axis.title = element_blank(),
legend.position = "none")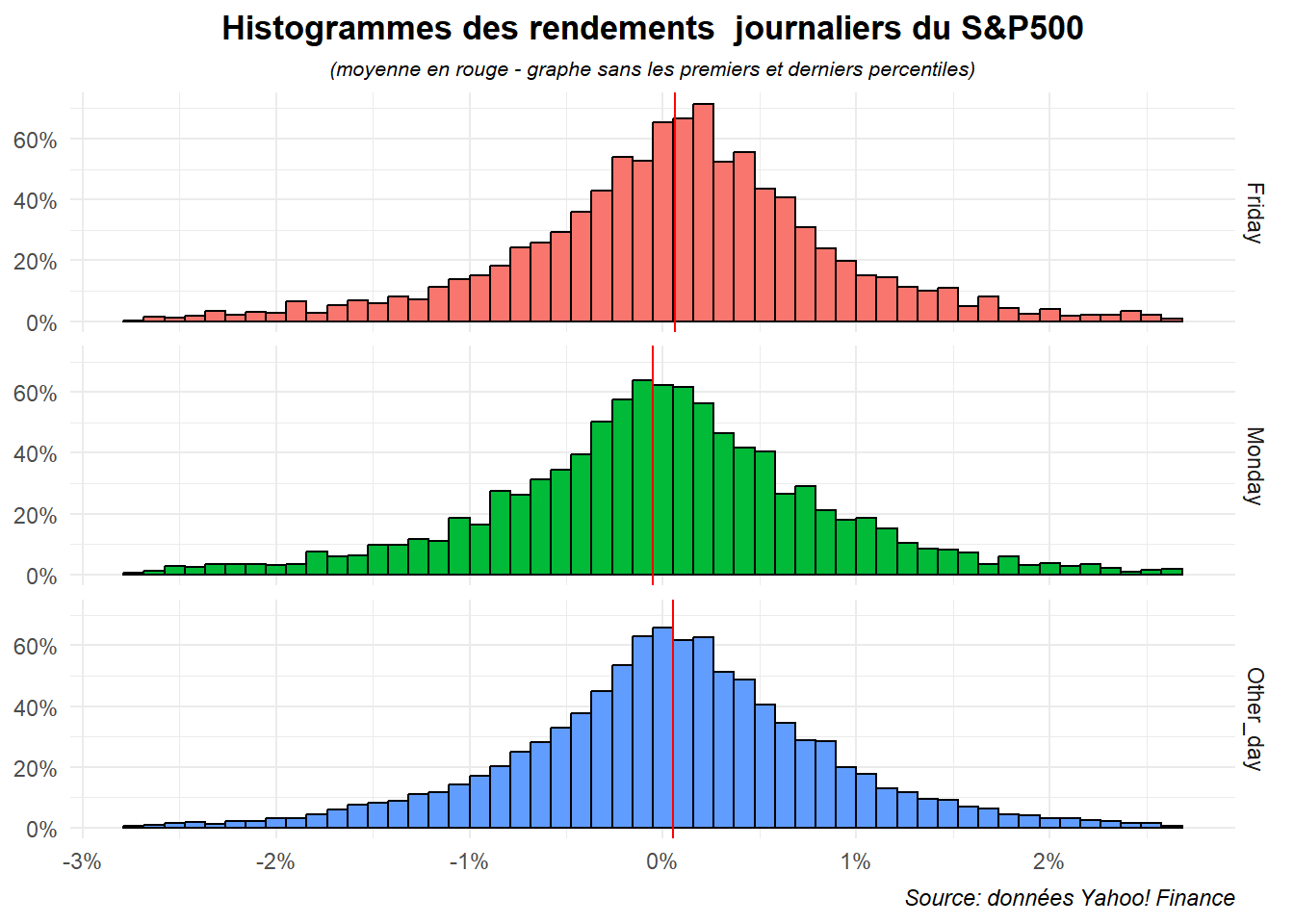
Le résultat en lui n’est pas mal mais on pourrait encore l’amélioré en ordonnant les graphes de manière à ce que lundi apparaisse en premier puis vendredi et enfin les autres jours. Profitons-en pour les passer en français.
dat<-dat %>%
mutate(jour_f=factor(jour,levels=c("Monday","Friday","Other_day"),
labels=c("Lundi","Vendredi","Les autres jours")))
dat_moy<-dat %>%
group_by(jour_f) %>%
summarise(moy_ret=mean(ret))
ggplot(data= filter(dat,
ret>=quantile(ret,probs=.01)&
ret<quantile(ret,probs=.99)),
aes(x=ret,fill=jour_f))+
geom_histogram(aes(y=after_stat(density)),bins=52,color='black')+
geom_vline(data=dat_moy,aes(xintercept = moy_ret),color='red')+
labs(title="Histogrammes des rendements journaliers du S&P500",
subtitle = "(moyenne en rouge - graphe sans les premiers et derniers percentiles)",
caption="Source: données Yahoo! Finance")+
scale_x_continuous(labels=label_percent(accuracy = 1))+
scale_y_continuous(labels=label_percent(scale=1))+
facet_grid(rows=vars(jour_f))+
theme_minimal()+
theme(
plot.title = element_text(hjust = 0.5,face='bold'),
plot.subtitle = element_text(hjust = 0.5,face='italic',size=8),
plot.caption = element_text(hjust = 1,face='italic'),
axis.title = element_blank(),
legend.position = "none")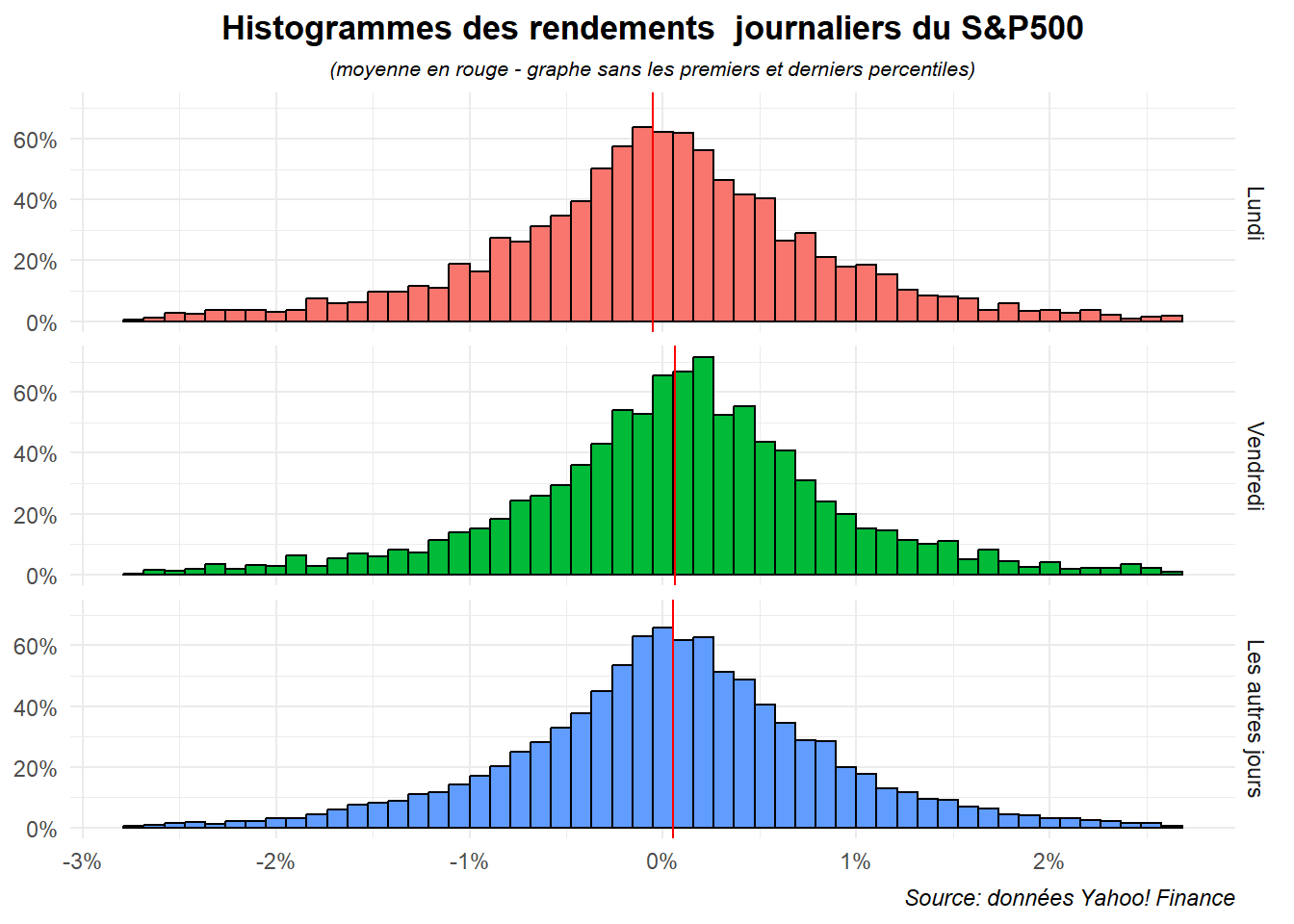
D’autres types d’histogrammes pourraient être mobilisés avec position dodge ou stack, mais ils donnent des résultats bien plus confus.
ggplot(data=filter(dat,
ret>=quantile(ret,probs=.01)&
ret<quantile(ret,probs=.99)),
aes(x=ret,fill=jour_f))+
geom_histogram(aes(y=after_stat(density)),bins=52,
position='dodge',color='black',linewidth=0.001)+
labs(title="Histogrammes des rendements journaliers du S&P500",
caption="Source: données Yahoo! Finance",
fill="Jours de la semaine")+
scale_x_continuous(labels=label_percent(accuracy = 1))+
scale_y_continuous(labels=label_percent(scale=1))+
theme_minimal()+
theme(
plot.title = element_text(hjust = 0.5,face='bold'),
plot.caption = element_text(hjust = 1,face='italic'),
axis.title = element_blank(),
legend.position = c(0.8,0.7))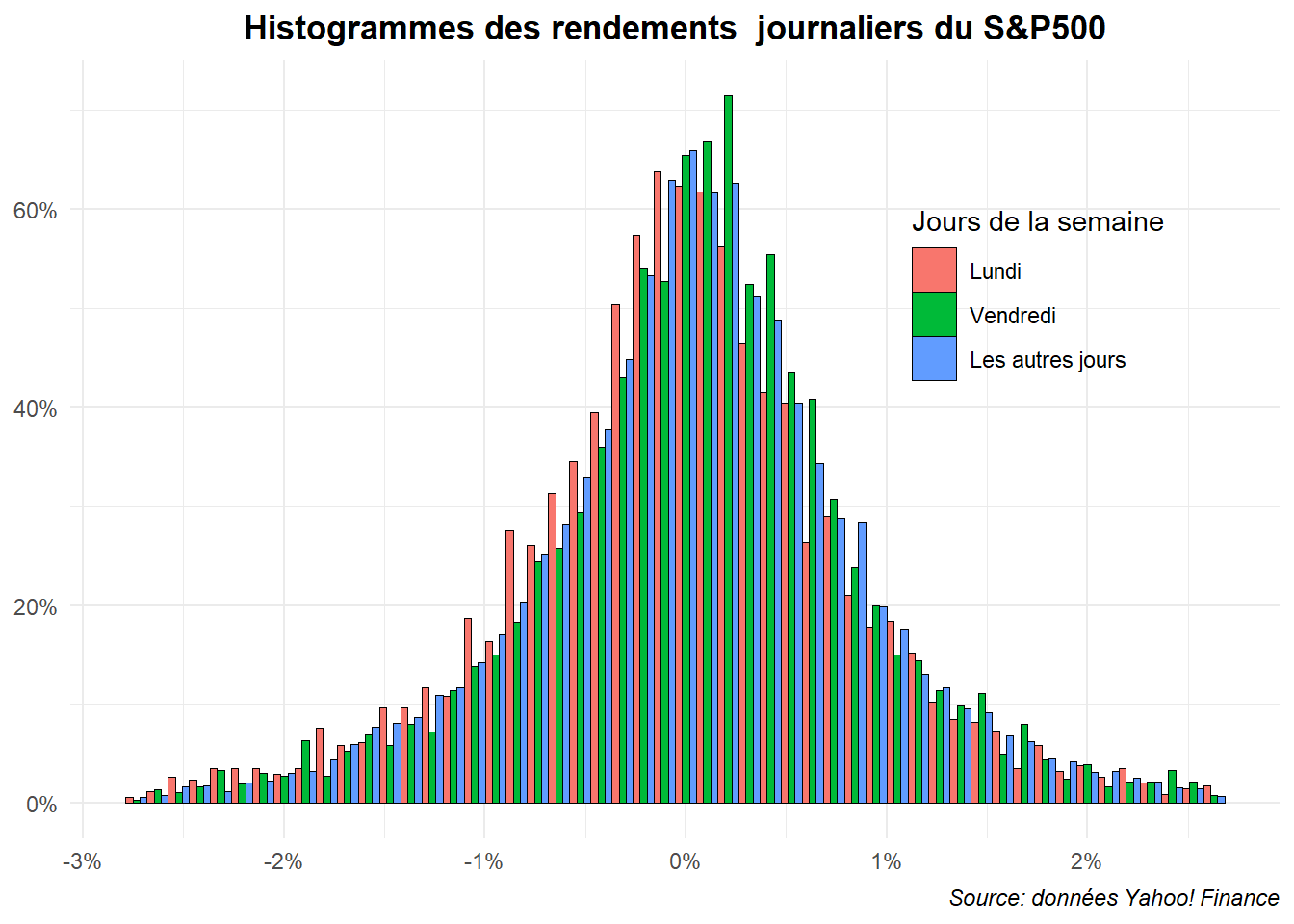
L’histogramme triple avec les trois séries juxtaposés (dodge) est clairement difficile à la lire. Voyons ce qu’il en est avec l’histogramme triple superposé.
ggplot(data=filter(dat,
ret>=quantile(ret,probs=.01)&
ret<quantile(ret,probs=.99)),
aes(x=ret,fill=jour_f))+
geom_histogram(aes(y=after_stat(density)),bins=52,
position='stack',color='black',linewidth=0.001)+
labs(title="Histogrammes des rendements journaliers du S&P500",
caption="Source: données Yahoo! Finance",
fill="Jours de la semaine")+
scale_x_continuous(labels=label_percent(accuracy = 1))+
scale_y_continuous(labels=label_percent(scale=1))+
theme_minimal()+
theme(
plot.title = element_text(hjust = 0.5,face='bold'),
plot.caption = element_text(hjust = 1,face='italic'),
axis.title = element_blank(),
legend.position = c(0.8,0.7))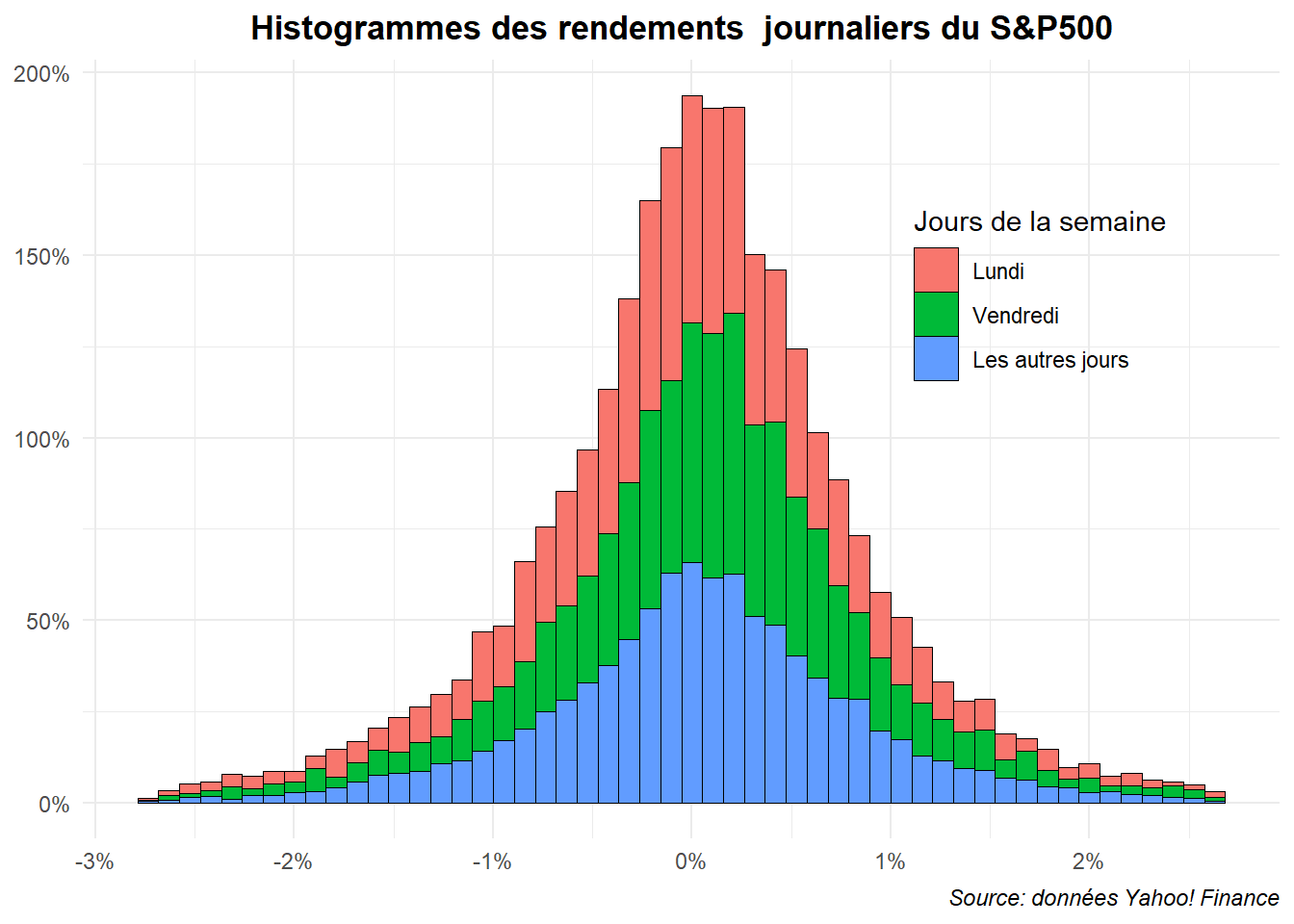
Ce dernier est encore plus illisible. Venons-en au graphe en pyramide. Ils ne permettent que de comparer des paires. Limitons nous, pour commencer, à l’opposition lundi contre les autres jours de la semaine. Commençons par l’établir en miroir.
ggplot(data=dat,aes(x=ret,fill=jour_f))+
geom_histogram(data=filter(dat,jour_f=="Lundi"&
ret>=quantile(ret,probs=.01)&
ret<quantile(ret,probs=.99)),
aes(x=ret,y=after_stat(density)),bins=52,color='black')+
geom_histogram(data=filter(dat,jour_f=="Les autres jours"&
ret>=quantile(ret,probs=.01)&
ret<quantile(ret,probs=.99)),
aes(x=ret,y=-after_stat(density)),bins=52,color='black')+
geom_vline(xintercept = dat_moy$moy_ret[dat_moy$jour_f=='Lundi'],
color='red')+
geom_vline(xintercept = dat_moy$moy_ret[dat_moy$jour_f=='Les autres jours'],
color='blue')+
labs(title="Histogrammes des rendements journaliers du S&P500",
subtitle = "Lundi(saumon-rouge) contre Mardi,Mercredi,Jeudi (vert-bleu)",
caption="Source: données Yahoo! Finance")+
scale_x_continuous(labels=label_percent(accuracy = 1))+
scale_y_continuous(breaks=c(-40,0,40),labels=c("40%","0%","40%"))+
theme_minimal()+
theme(plot.title = element_text(hjust = 0.5,face='bold'),
plot.subtitle = element_text(hjust = 0.5,face='italic',size=8),
plot.caption = element_text(hjust = 1,face='italic'),
axis.title = element_blank(),
legend.position = "none")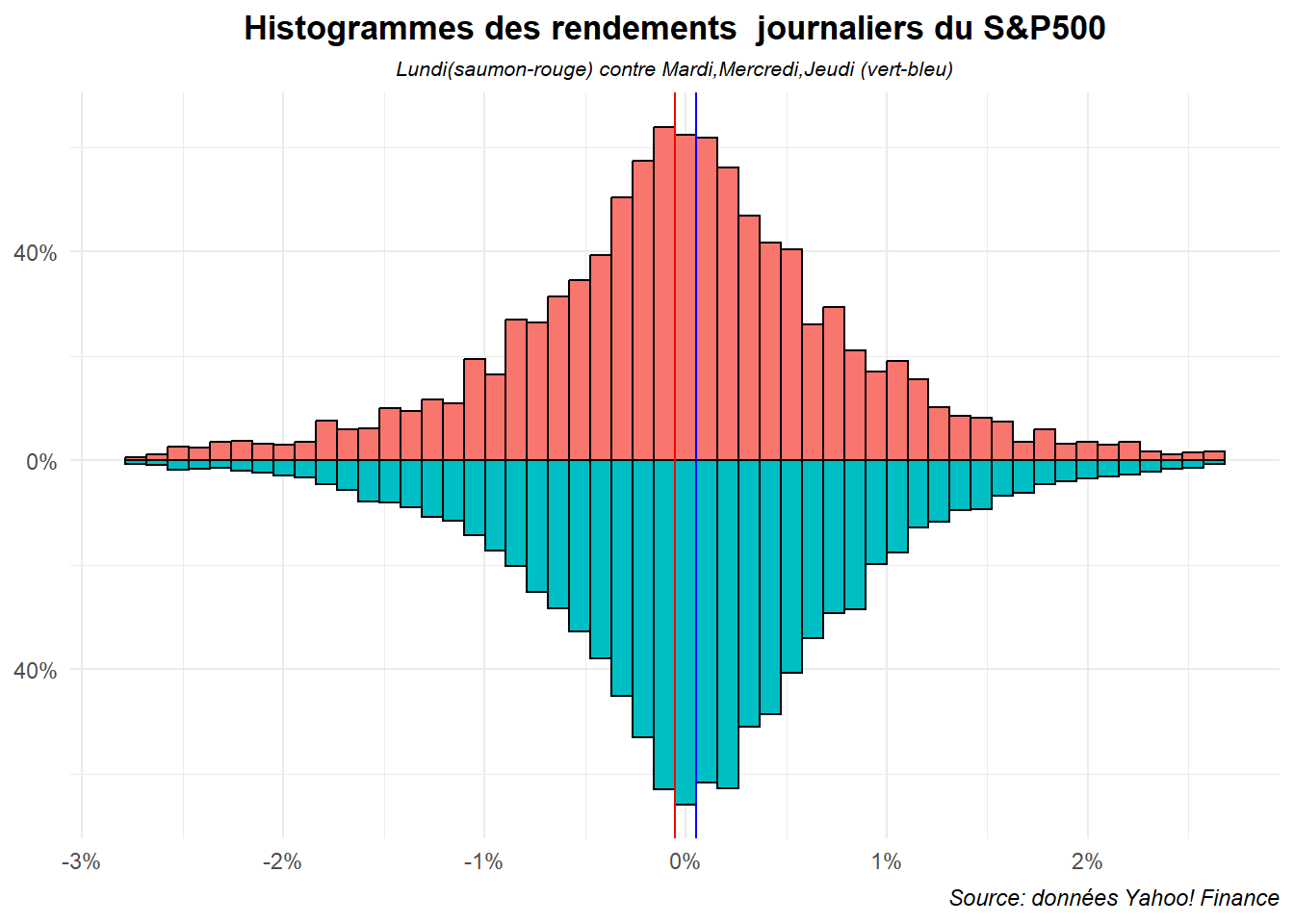
Pour obtenir une pyramide, il suffit de renverser le système de coordonnés avec coord_flip().
ggplot(data=dat,aes(x=ret,fill=jour_f))+
geom_histogram(data=filter(dat,jour_f=="Lundi"&
ret>=quantile(ret,probs=.01)&
ret<quantile(ret,probs=.99)),
aes(x=ret,y=after_stat(density)),bins=52,color='black')+
geom_histogram(data=filter(dat,jour_f=="Les autres jours"&
ret>=quantile(ret,probs=.01)&
ret<quantile(ret,probs=.99)),
aes(x=ret,y=-after_stat(density)),bins=52,color='black')+
geom_vline(xintercept = dat_moy$moy_ret[dat_moy$jour_f=='Lundi'],
color='red')+
geom_vline(xintercept = dat_moy$moy_ret[dat_moy$jour_f=='Les autres jours'],
color='blue')+
labs(title="Histogrammes des rendements journaliers du S&P500",
subtitle = "Lundi(saumon-rouge) contre Mardi,Mercredi,Jeudi (vert-bleu)",
caption="Source: données Yahoo! Finance")+
scale_x_continuous(labels=label_percent(accuracy = 1))+
scale_y_continuous(breaks=c(-40,0,40),labels=c("40%","0%","40%"))+
coord_flip()+
theme_minimal()+
theme(plot.title = element_text(hjust = 0.5,face='bold'),
plot.subtitle = element_text(hjust = 0.5,face='italic',size=8),
plot.caption = element_text(hjust = 1,face='italic'),
axis.title = element_blank(),
legend.position = "none")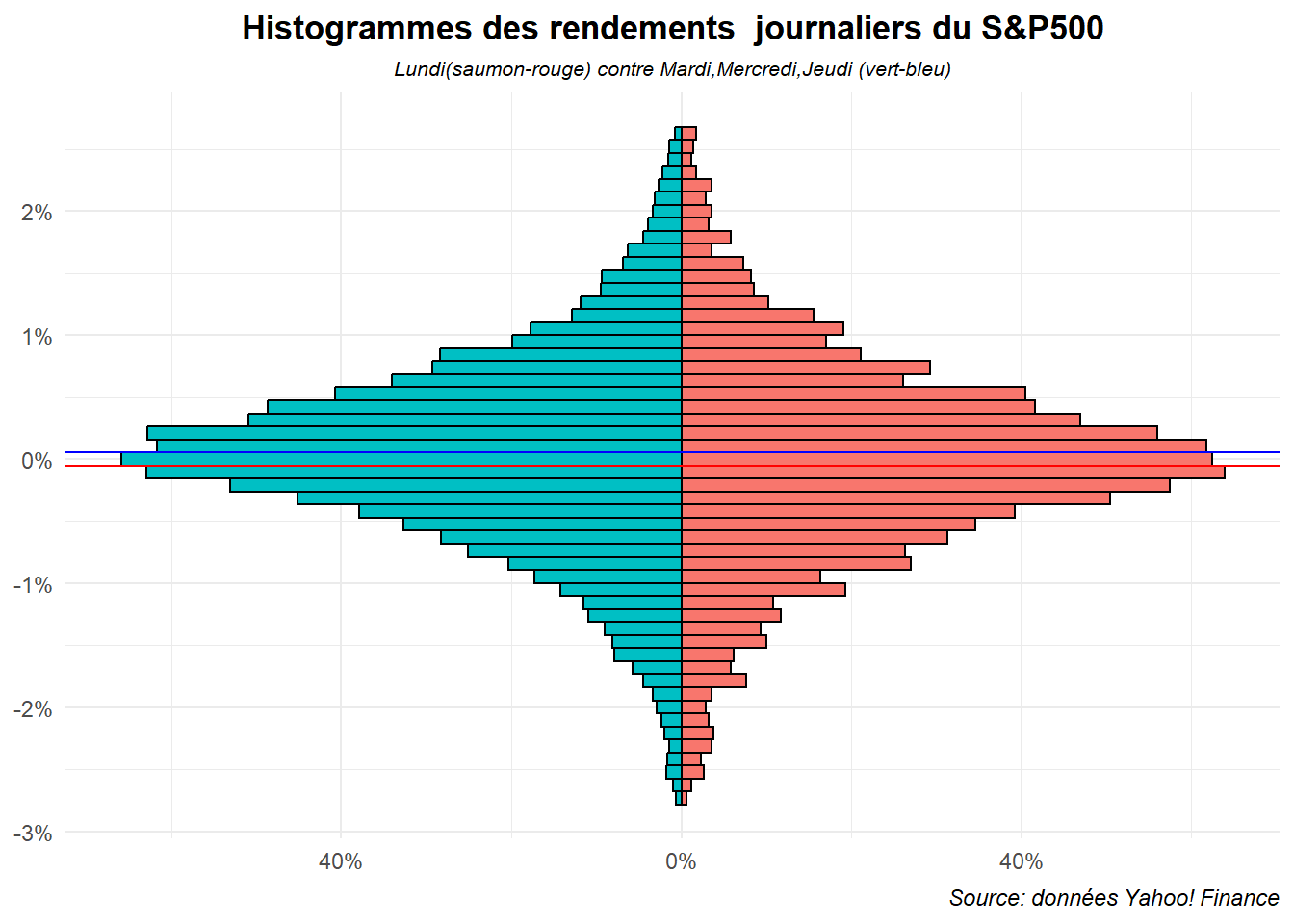
Voilà nous avons un histogramme en pyramide assez claire. Réalisons le même graphe pour le vendredi et mettons le en regard de celui-ci. Pour cela, nous utiliserons le package patchwork. Créons d’abord une fonction permettant de générer des graphes rapidement.
graph_pyr<-function(d,jr,titr){
ggplot(data=d,aes(x=ret,fill=jour_f))+
geom_histogram(data=filter(d,jour_f==jr&
ret>=quantile(ret,probs=.01)&
ret<quantile(ret,probs=.99)),
aes(x=ret,y=after_stat(density)),bins=52,color='black')+
geom_histogram(data=filter(d,jour_f=="Les autres jours"&
ret>=quantile(ret,probs=.01)&
ret<quantile(ret,probs=.99)),
aes(x=ret,y=-after_stat(density)),bins=52,color='black')+
labs(title=titr)+
scale_x_continuous(labels=label_percent(accuracy = 1))+
scale_y_continuous(breaks=c(-40,0,40),
labels=c("40%","0%","40%"))+
coord_flip()+
theme_minimal()+
theme(
plot.title = element_text(hjust = 0.5,face='bold',size=8),
axis.title = element_blank(),
legend.position = "none")}Ceci fait, on peut réunir la pyramide associée à l’effet Lundi et celle associée à l’effet Vendredi. Ajoutons à ceci quelques mises en forme
g1<-graph_pyr(dat,'Lundi',
'Mardi,Mercredi,Jeudi (vert) vs Lundi(saumon)')
g2<-graph_pyr(dat,'Vendredi',
'Mardi,Mercredi,Jeudi (vert) vs Vendredi(saumon)')
g1+g2 + plot_annotation(
title = 'Pyramides des rendements journaliers du S&P500',
subtitle = 'Effet weekend (Full sample - Winsorisé 1%-99%)',
caption = 'Source: données Yahoo! Finance',
theme = theme(plot.title = element_text(hjust = 0.5,face='bold'),
plot.subtitle = element_text(hjust = 0.5,face='bold'),
plot.caption = element_text(hjust = 1,face='italic')))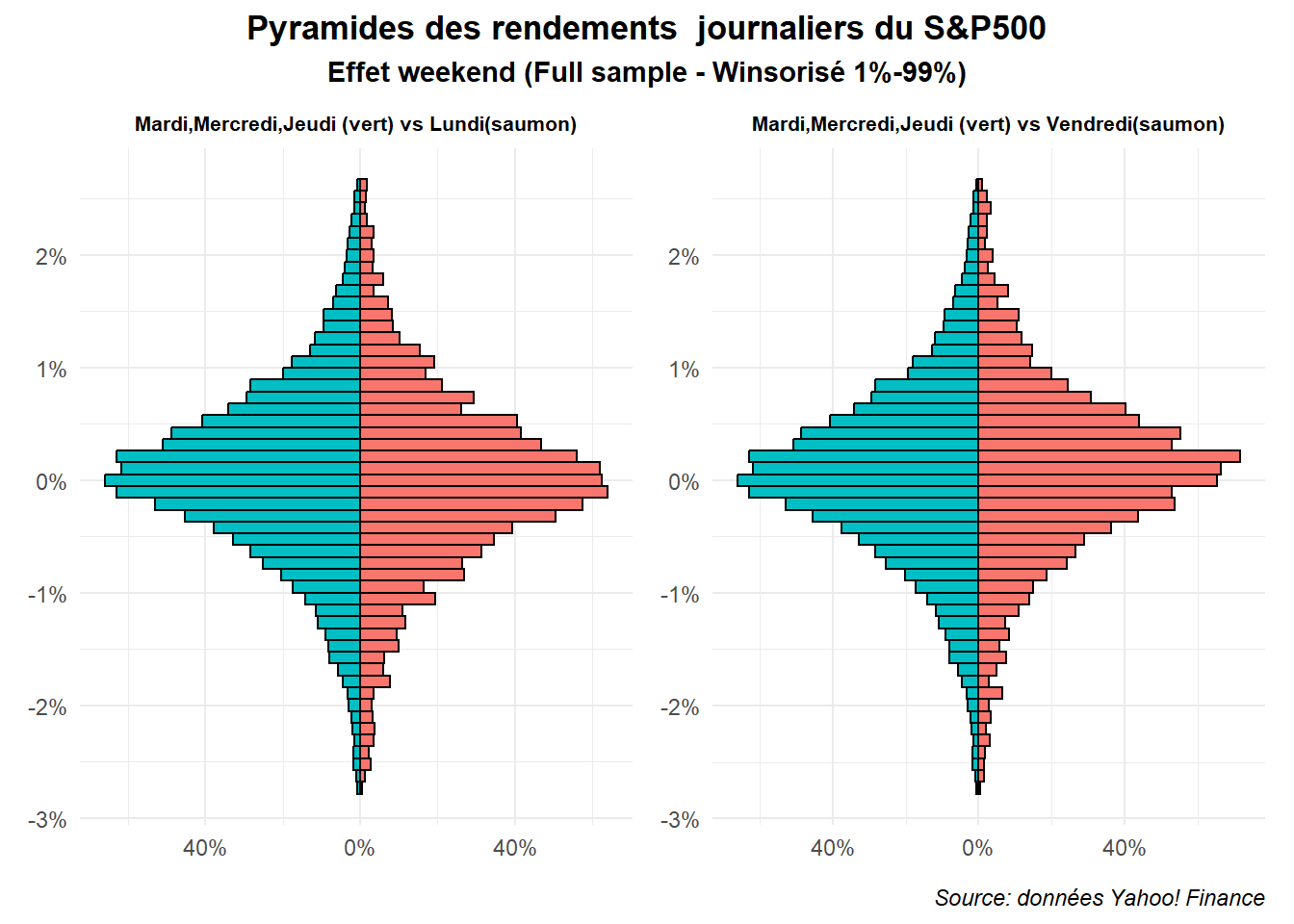
La même chose peut être réalisée avec l’échantillon de French (1953-1977).
g1<-graph_pyr(filter(dat,date>date("1953/01/01")&
date<date("1977/12/31")),
'Lundi','Mardi,Mercredi,Jeudi (vert) vs Lundi(saumon)')
g2<-graph_pyr(filter(dat,date>date("1953/01/01")&
date<date("1977/12/31")),
'Vendredi','Mardi,Mercredi,Jeudi (vert) vs Vendredi(saumon)')
g1+g2 + plot_annotation(
title = 'Pyramides des rendements journaliers du S&P500',
subtitle = 'Effet weekend - French (1953-1977) - Winsorisé 1%-99%',
caption = 'Source: données Yahoo! Finance',
theme = theme(plot.title = element_text(hjust = 0.5,face='bold'),
plot.subtitle = element_text(hjust = 0.5,face='bold'),
plot.caption = element_text(hjust = 1,face='italic')))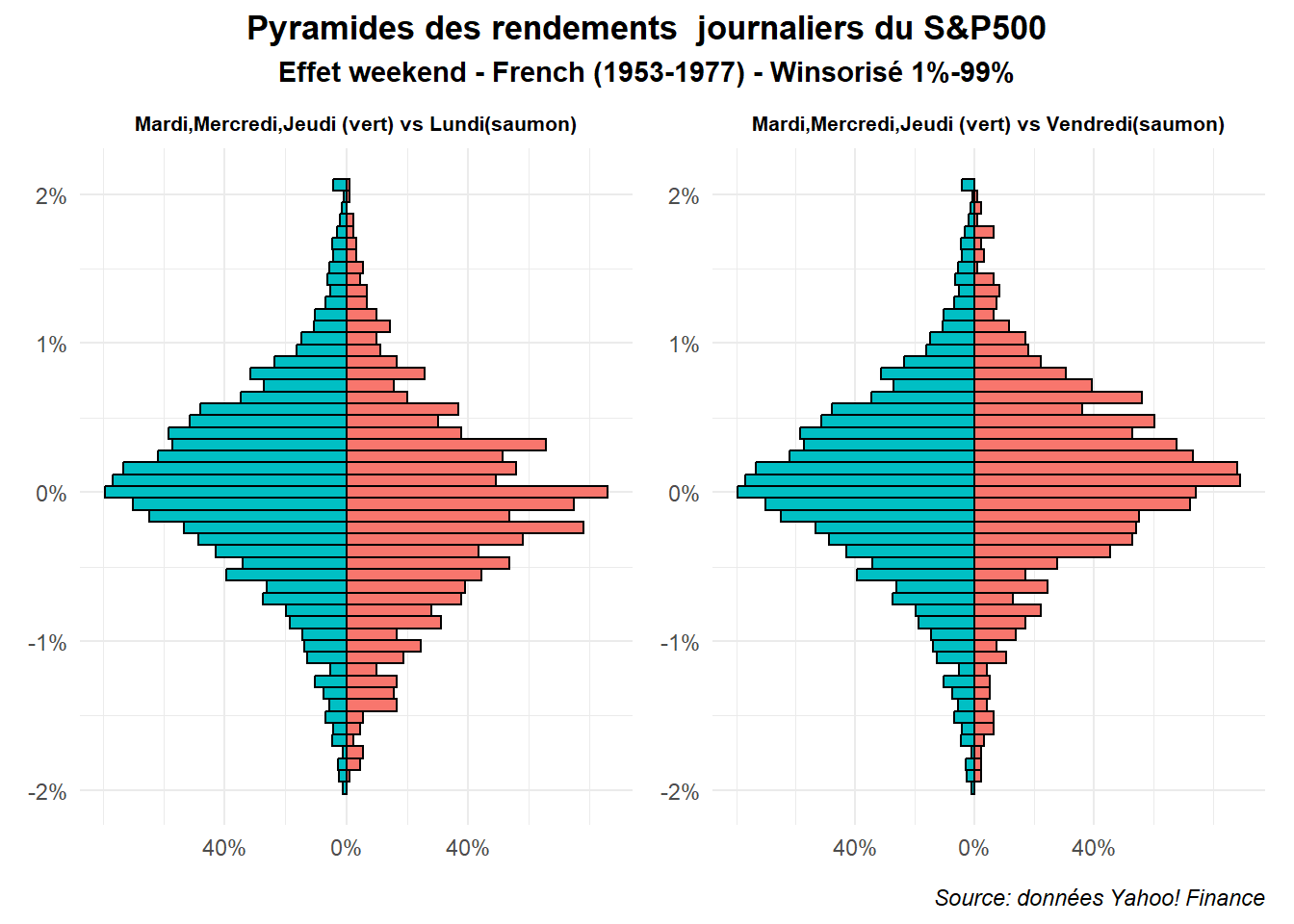
On est alors confronté à des différences plus marquées. Cela n’est pas le cas pour la période post 2000 comme on peut le voir dans la figure réalisée à partir des données associées.
g1<-graph_pyr(filter(dat,date>date("2000/01/01")),
'Lundi','Mardi,Mercredi,Jeudi (vert) vs Lundi(saumon)')
g2<-graph_pyr(filter(dat,date>date("2000/01/01")),
'Vendredi','Mardi,Mercredi,Jeudi (vert) vs Vendredi(saumon)')
g1+g2 + plot_annotation(
title = 'Pyramides des rendements journaliers du S&P500',
subtitle = 'Effet weekend - après 2000 - Winsorisé 1%-99',
caption = 'Source: données Yahoo! Finance',
theme = theme(plot.title = element_text(hjust = 0.5,face='bold'),
plot.subtitle = element_text(hjust = 0.5,face='bold'),
plot.caption = element_text(hjust = 1,face='italic')))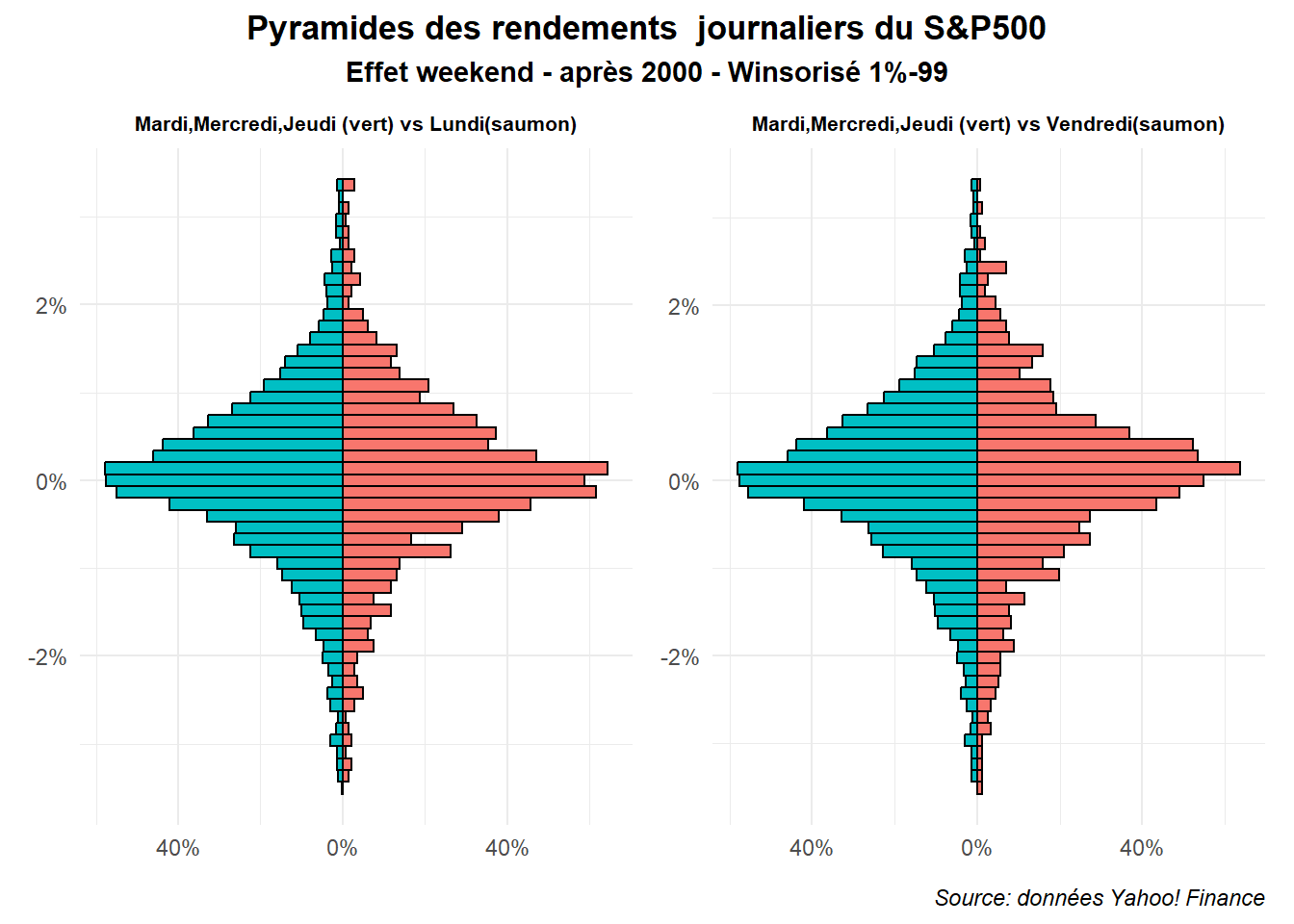
Le pyramide graphe permet de très facilement comparer deux distributions. C’est à la fois sa force et sa limite. Nous verrons par la suite des graphes permettant d’illustrer la comparaison de plus deux distributions.