Ce post ouvre une nouvelle partie de la série GT. Après avoir traité des représentations utilisées pour rendre compte des variables discrètes et de celles utilisées pour les séries temporelles, nous traitons maintenant de la manière de représenter les distributions de variables continues. Le premier type de graphe que nous aborderons est un grand classique. Il s’agit de l’histogramme. Celui consiste en une série de barres accolées à la manière d’un bar plot classique. La hauteur des barres représente le nombre d’observations (ou leurs fréquences) pour qui la valeur de la variable illustrée est comprise dans un intervalle donné.
Construisons-en un. Mais avant chargeons les packages que nous allons mobiliser: le classique tidyverse; scales, pour les axes; patchwork, pour présenter plusieurs graphe ensemble; tidyquant, pour charger des données financières; tsibble, pour gérer certaines manipulations de dates.
library(tidyverse)
library(scales)
library(patchwork)
library(tidyquant)
library(tsibble)Nous travaillerons à partir de l’indice NASDAQ 100. Il s’agira d’établir l’histogramme des rendements pour différentes durées. L’indice commence avec une valeur de 100 le 31 janvier 1985. Utilisons la fonction tq_get() du package tidyquant pour obtenir les données. Celle permet d’obtenir l’information à partir du ticker d’un titre ou d’un indice. Le ticker du NASDAQ 100 est ^NDX.
dat<-tq_get("^NDX",from="1985-01-31")
glimpse(dat)## Rows: 9,640
## Columns: 8
## $ symbol <chr> "^NDX", "^NDX", "^NDX", "^NDX", "^NDX", "^NDX", "^NDX", "^NDX…
## $ date <date> 1985-10-01, 1985-10-02, 1985-10-03, 1985-10-04, 1985-10-07, …
## $ open <dbl> 110.620, 112.140, 110.840, 110.870, 110.075, 108.200, 107.160…
## $ high <dbl> 112.160, 112.540, 111.185, 110.870, 110.135, 108.270, 108.990…
## $ low <dbl> 110.565, 110.780, 110.120, 109.855, 108.175, 106.750, 107.115…
## $ close <dbl> 112.140, 110.825, 110.870, 110.075, 108.200, 107.160, 108.630…
## $ volume <dbl> 153160000, 164640000, 147300000, 147900000, 128640000, 144100…
## $ adjusted <dbl> 112.140, 110.825, 110.870, 110.075, 108.200, 107.160, 108.630…On obtenir une data frame de 9636 observations reprenant différentes valeurs de l’indice pour différentes journées de cotations. Voyons les dates de début et de fin de la série.
c(debut=min(dat$date),fin=max(dat$date))## debut fin
## "1985-10-01" "2023-12-29"Les données obtenues débutent le 1er novembre 1985 (nous n’avons pas le début de l’indice mais on est pas loin) et se terminent le 22 décembre 2022. Limitons-nous au date et à la valeur de clôture.
dat<-dat %>%
select(date,close)Calculons le rendement journalier simple.
dat<-dat %>% mutate(ret=close/lag(close)-1,
ret_c=log(close/lag(close)))
summary(dat$ret)## Min. 1st Qu. Median Mean 3rd Qu. Max. NA's
## -0.1507762 -0.0067142 0.0012126 0.0006557 0.0083705 0.1877131 1Le calcul a généré une valeur manquante pour la première observation. Supprimons-la.
dat_<-dat %>%
drop_na()Maintenant que les données sont prêtes, nous pouvons générer notre premier histogramme. Pour cela, nous mobilisons simplement le geom_histogram().
ggplot(data=dat_,aes(x=ret))+
geom_histogram()## `stat_bin()` using `bins = 30`. Pick better value with `binwidth`.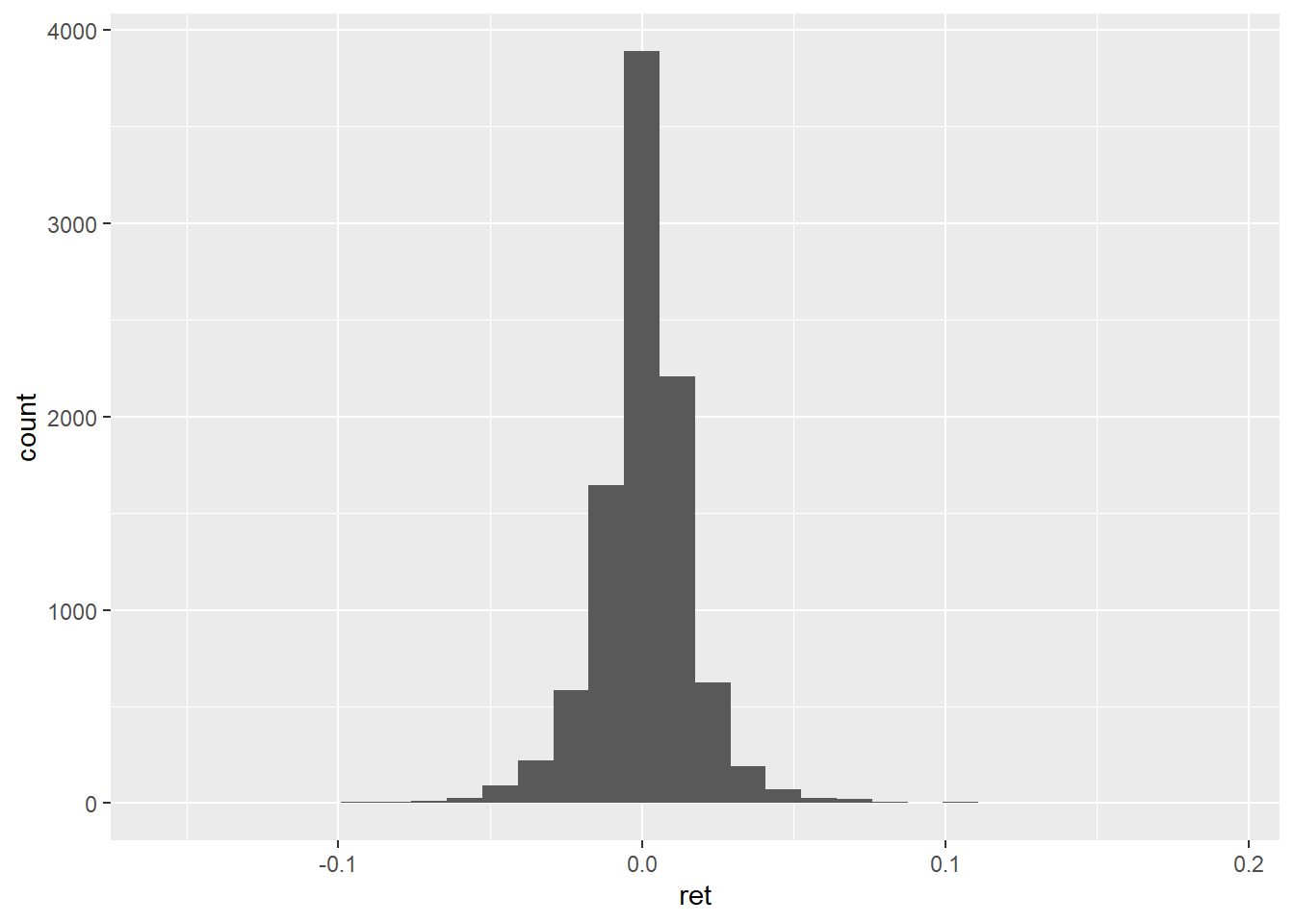
Le résultat n’est pas terrible mais on peut améliorer les choses avec un peu de travail. Commençons par traiter le message généré. Le graphe par défaut est établi avec 30 intervalles (bins) ce qui peut ne pas être adapté.
Générons une bordure blanche pour nos barres avec l’option color et modifions le nombre d’intervalles avec l’option bins. Générons-en 100.
ggplot(data=dat_,aes(x=ret))+
geom_histogram(color='white',bins = 100)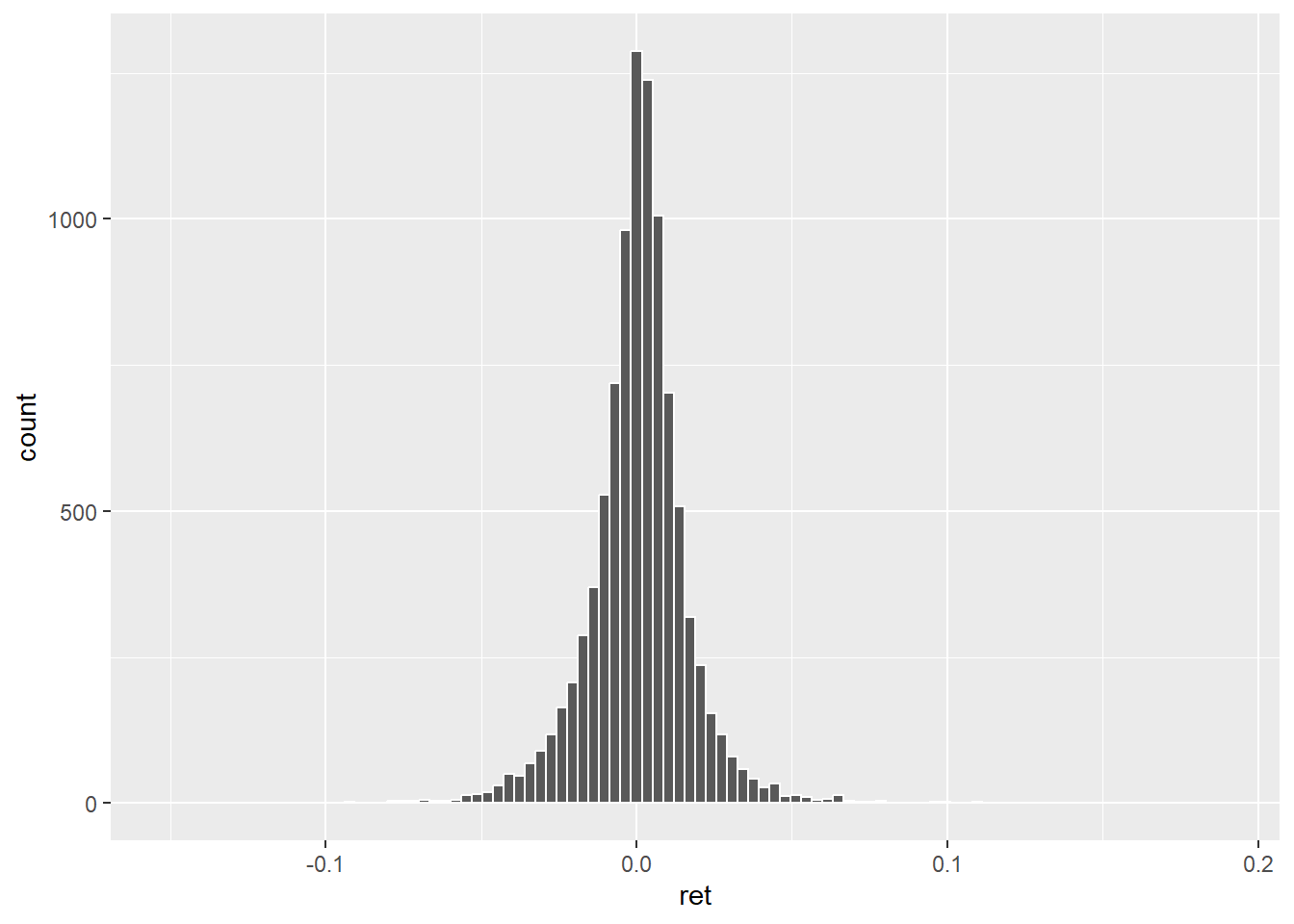
C’est un peu mieux mais le choix du nombre d’intervalles reste arbitraire. Quelques règles empiriques peuvent nous aider dans ce choix néanmoins leurs résultats devra être évalués au regard de la clarté de la représentation générée.
La règle de Sturges \(K=1+log_2(N)\) où K est le nombre d’intervalles et N le nombre d’observation.
1+log(9636,2)## [1] 14.23422On a alors.
ggplot(data=dat_,aes(x=ret))+
geom_histogram(color='white',bins = 15)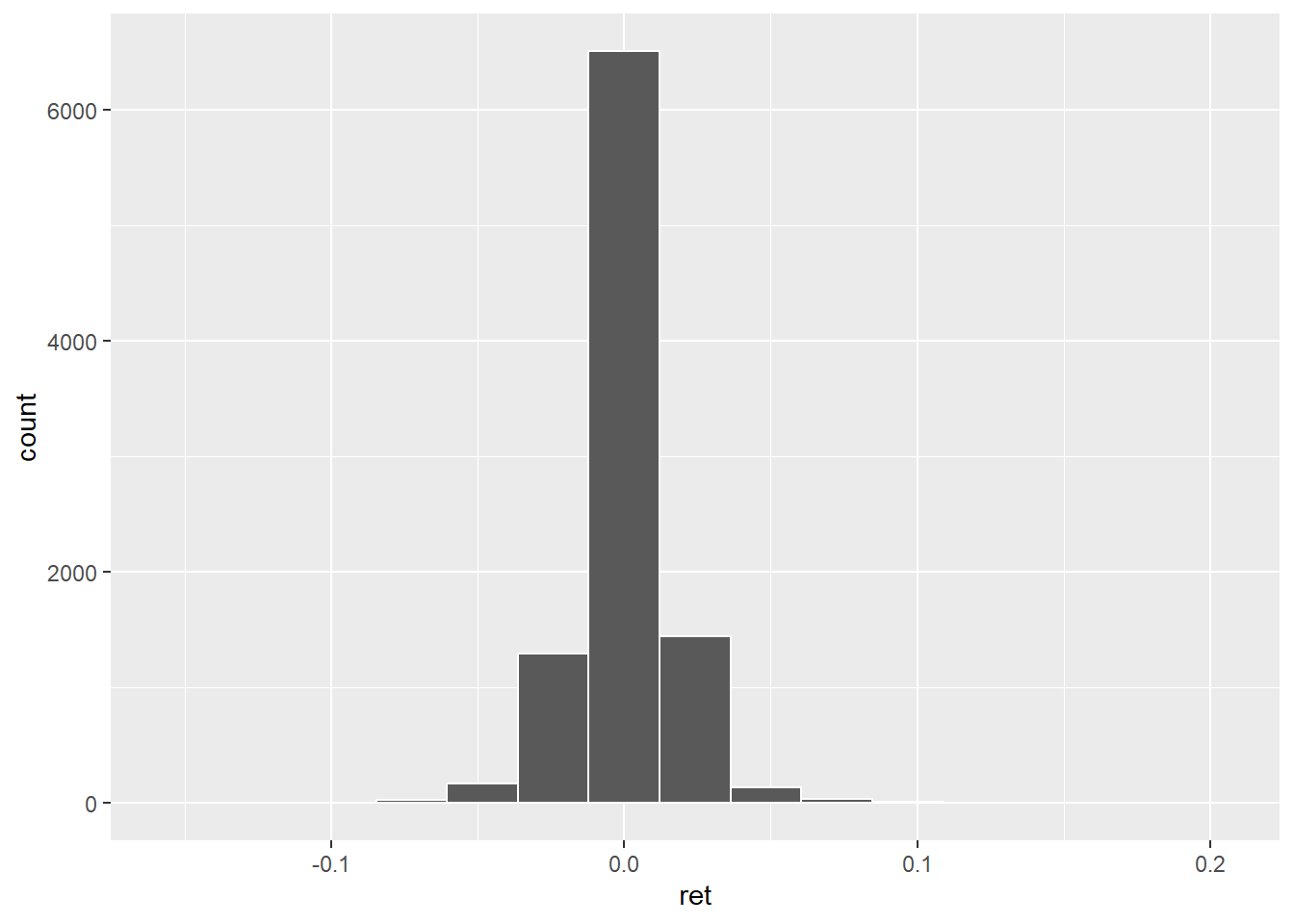
La règle de Rule \(K=1+\sqrt[3]{N}\).
2*9635^(1/3)## [1] 42.55794On a alors.
ggplot(data=dat_,aes(x=ret))+
geom_histogram(color='white',bins = 43)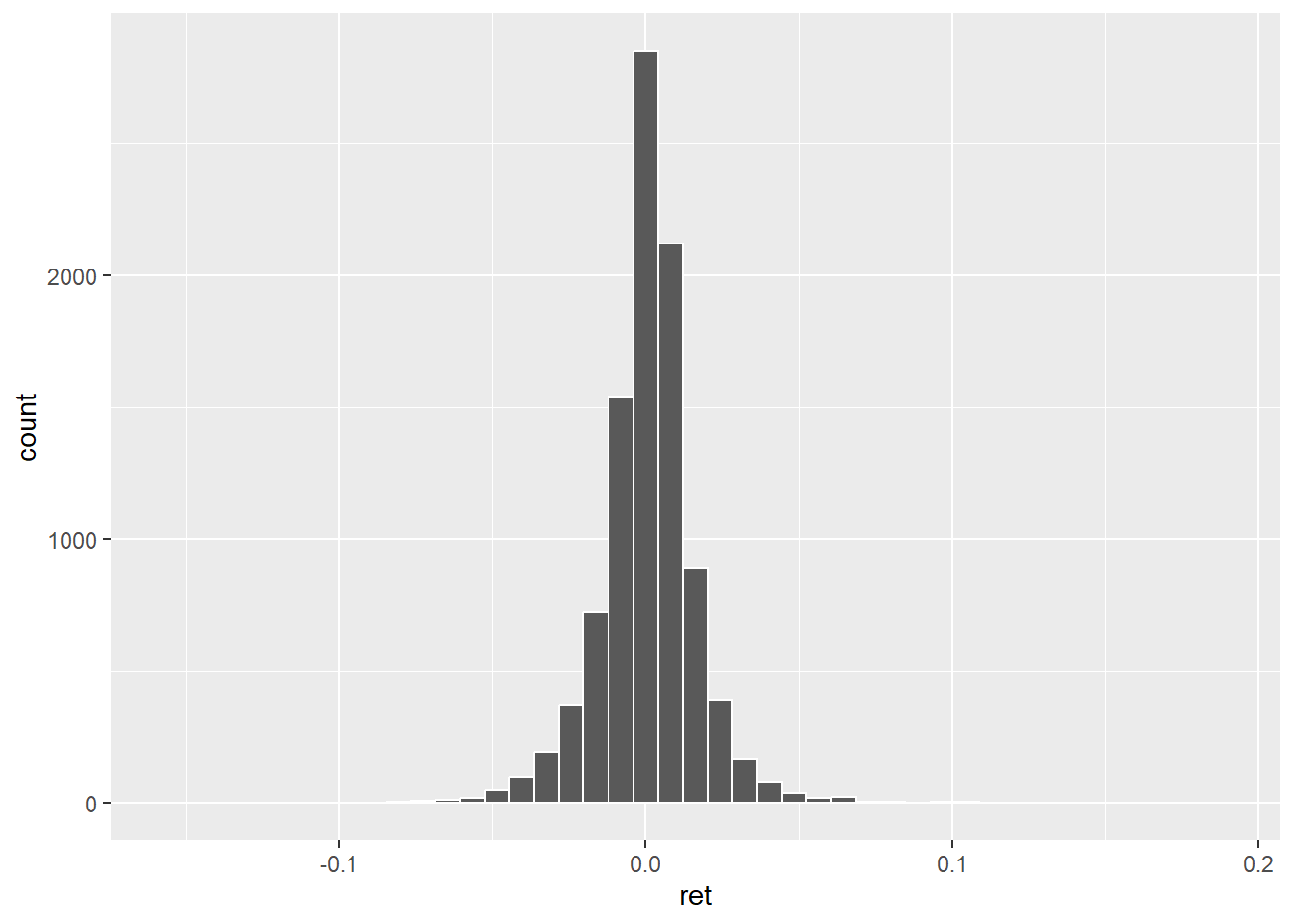
Une autre règle propose simplement de prendre la racine carré du nombre d’observations.
sqrt(9635)## [1] 98.15804Cela donne le graphe suivant.
ggplot(data=dat_,aes(x=ret))+
geom_histogram(color='white',bins = 98)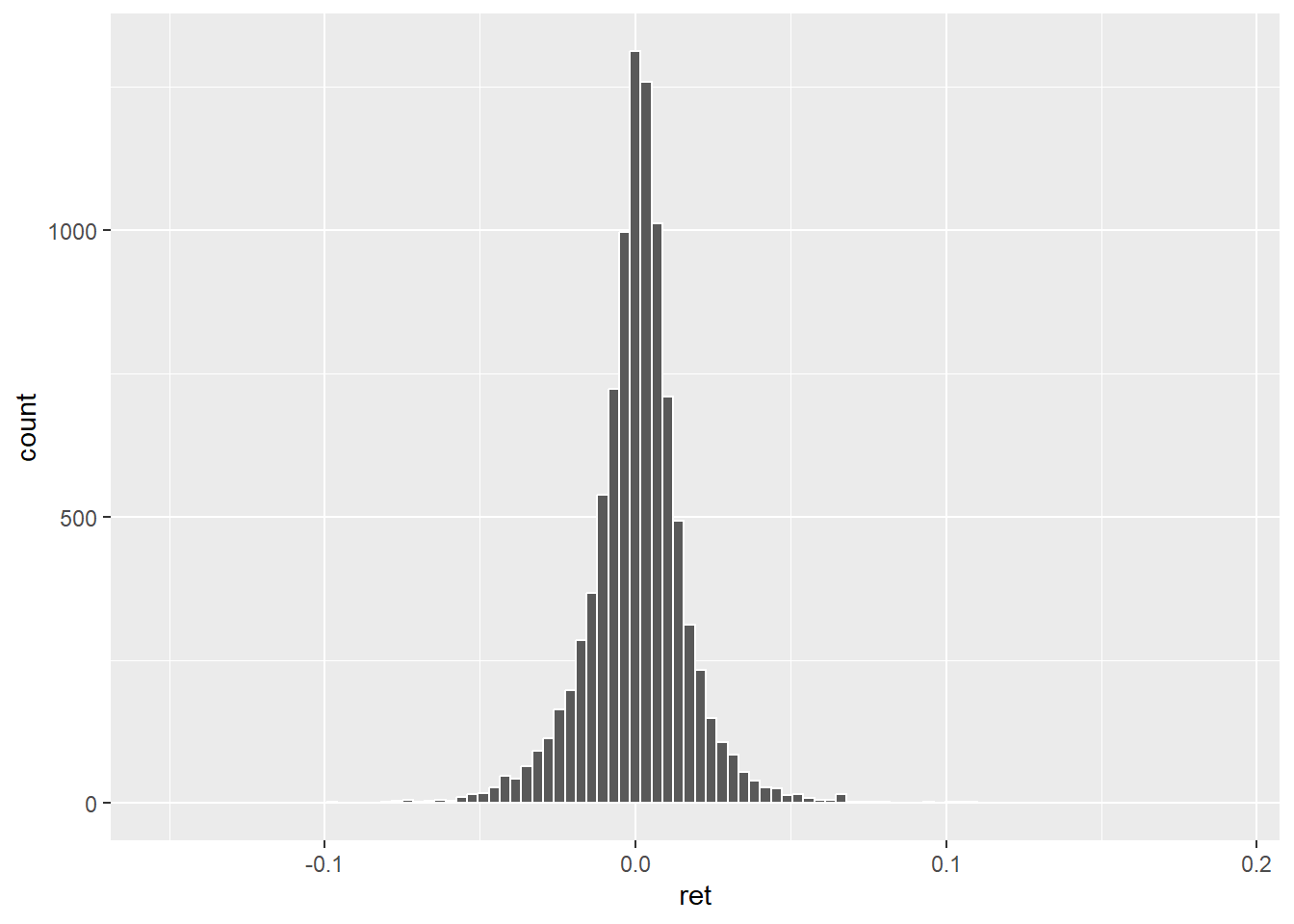
J’ai tendance à préférer cette dernière solution restons donc dessus. Poursuivons notre mise en forme avec un changement de thème, l’ajout d’un titre et d’autres annotations.
ggplot(data=dat_,aes(x=ret))+
geom_histogram(color='white',bins = 98)+
labs(title="Indice NASDAQ 100",
subtitle="à la clôture - 2 nov. 1985 : 22 dec. 2023",
caption="Source: GoogleFinance",
x="Rendements Journaliers",
y="Nb. obs.")+
scale_x_continuous(labels = label_percent())+
theme_minimal()+
theme(
plot.title = element_text(hjust=0.5,face='bold'),
plot.subtitle = element_text(hjust=0.5,face='italic')
)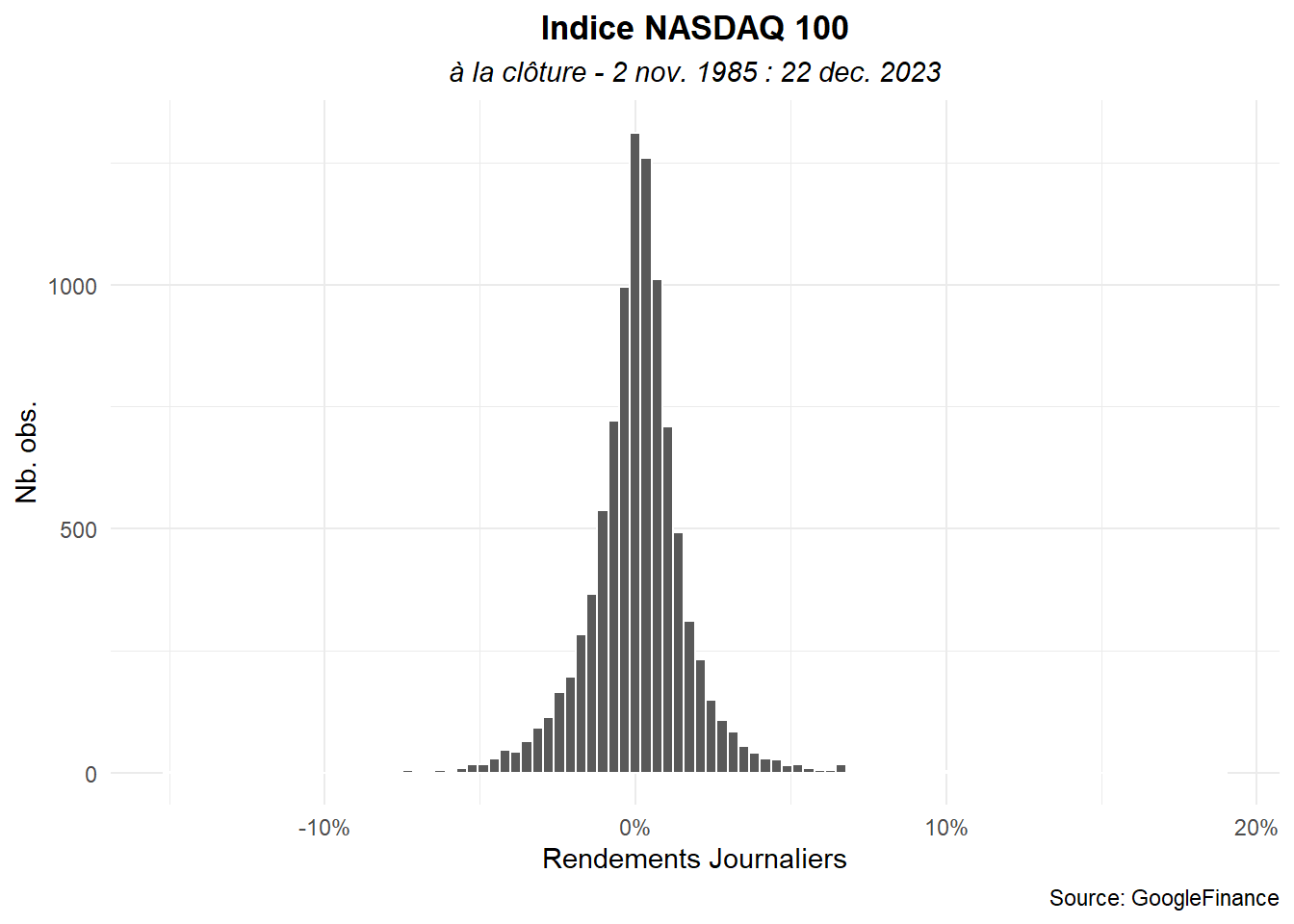
Le graphe est plus élégant mais il reste un problème important les quelques valeurs forts extrêmes sont peu visibles. Pour améliorer les choses, passons les lignes autour des barres en noire, réduisons leur épaisseur et marquons les valeurs observées sur l’axes des abscisses en utilisant le geom_rug().
ggplot(data=dat_,aes(x=ret))+
geom_histogram(color='black',linewidth=0.001,bins = 98)+
geom_rug()+
labs(title="Indice NASDAQ 100",
subtitle="à la clôture - 2 nov. 1985 : 22 dec. 2023",
caption="Source: GoogleFinance",
x="Rendements Journaliers",
y="Nb. obs.")+
scale_x_continuous(labels = label_percent())+
theme_minimal()+
theme(
plot.title = element_text(hjust=0.5,face='bold'),
plot.subtitle = element_text(hjust=0.5,face='italic')
)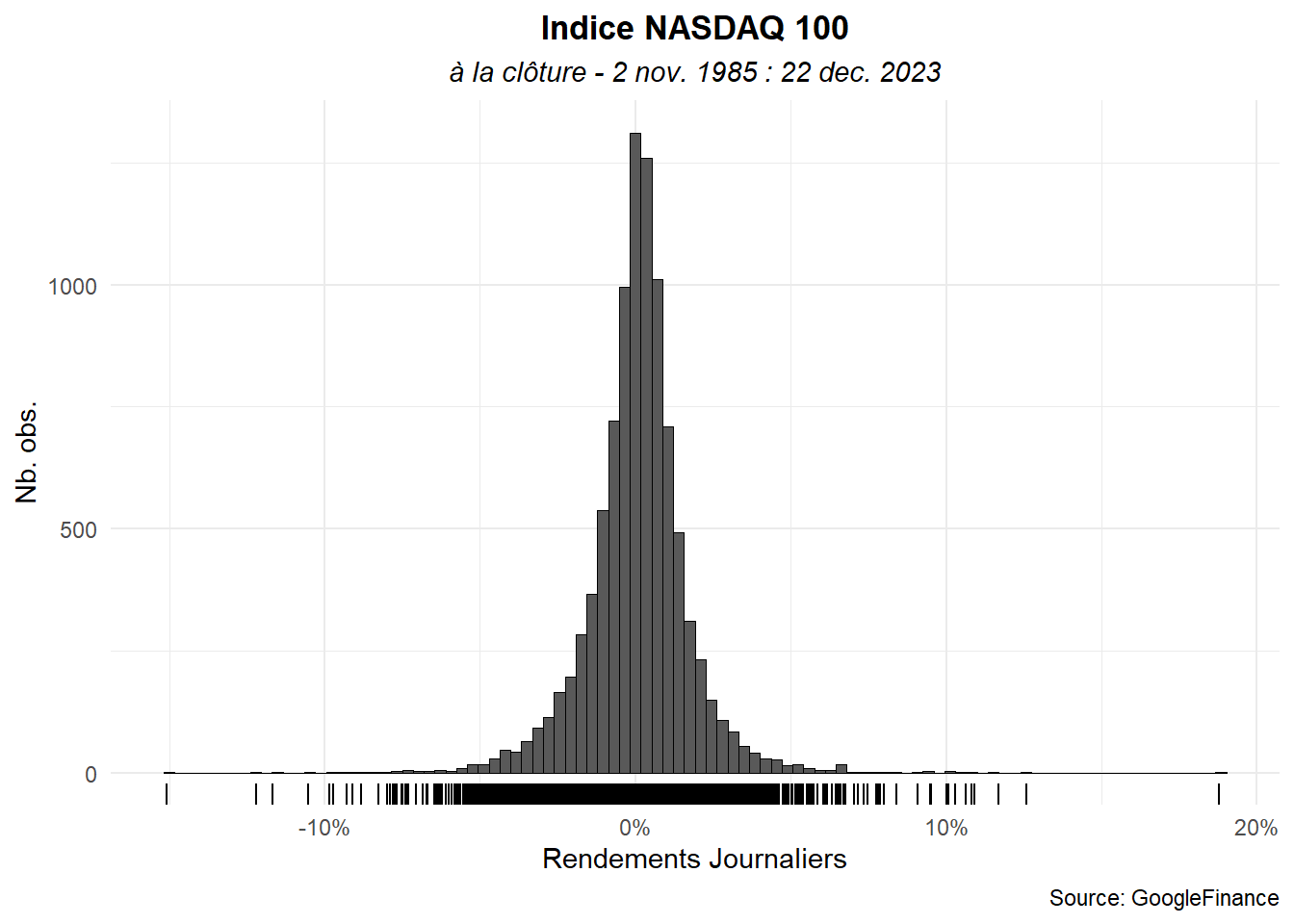
Le résultat est satisfaisant. Nous pourrions nous arrêter là. Néanmoins, il serait intéressant de marquer le rendement moyenne et de permettre la comparaison de l’histogramme avec la distribution normale correspondant aux données.
Utilisons geom_vline() pour la moyenne. Optons une ligne en pointillées rouges.
ggplot(data=dat_,aes(x=ret))+
geom_histogram(color='black',linewidth=0.001,bins = 98)+
geom_rug()+
geom_vline(aes(xintercept = mean(ret)),
color='red',linetype = "dashed")+
labs(title="Indice NASDAQ 100",
subtitle="à la clôture - 2 nov. 1985 : 22 dec. 2023",
caption="Source: GoogleFinance",
x="Rendements Journaliers",
y="Nb. obs.")+
scale_x_continuous(labels = label_percent())+
theme_minimal()+
theme(
plot.title = element_text(hjust=0.5,face='bold'),
plot.subtitle = element_text(hjust=0.5,face='italic')
)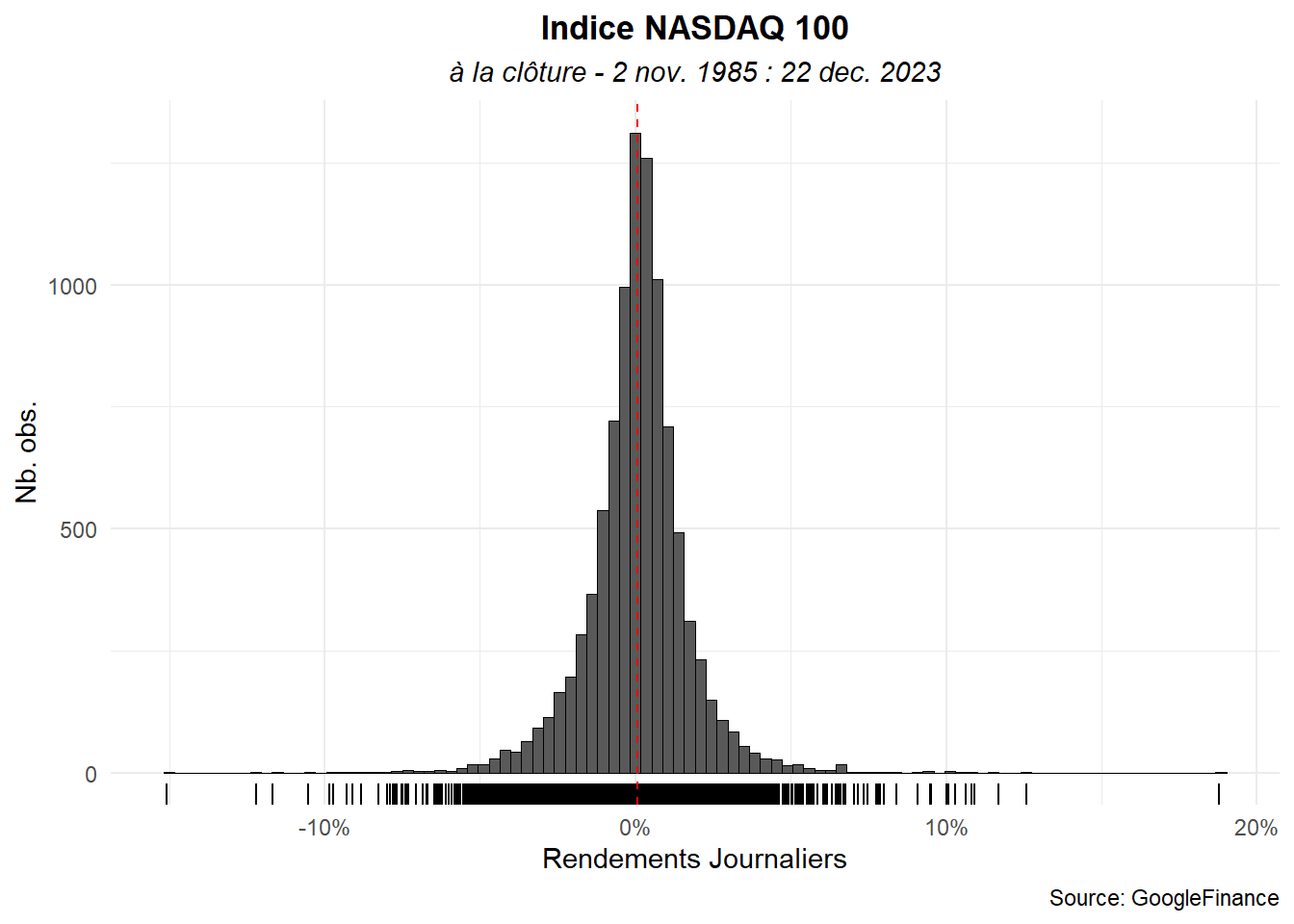
Pour la distribution normale, passons l’histogramme en densité et marquons la fonction d’une ligne violette pleine. Traçons-la en utilisant stat_function() avec fun égale dnorm.
ggplot(data=dat_,aes(x=ret))+
geom_histogram(aes(y=after_stat(density)),
color='black',linewidth=0.001,
bins = 98)+
geom_rug()+
geom_vline(aes(xintercept = mean(ret)),
color='red',linetype = "dashed")+
stat_function(fun=dnorm,
args=list(mean(dat_$ret),sd(dat_$ret)),
color='purple')+
labs(title="Indice NASDAQ 100",
subtitle="à la clôture - 2 nov. 1985 : 22 dec. 2023",
caption="Source: GoogleFinance",
x="Rendements Journaliers",
y="Densité")+
scale_x_continuous(labels = label_percent())+
theme_minimal()+
theme(
plot.title = element_text(hjust=0.5,face='bold'),
plot.subtitle = element_text(hjust=0.5,face='italic')
)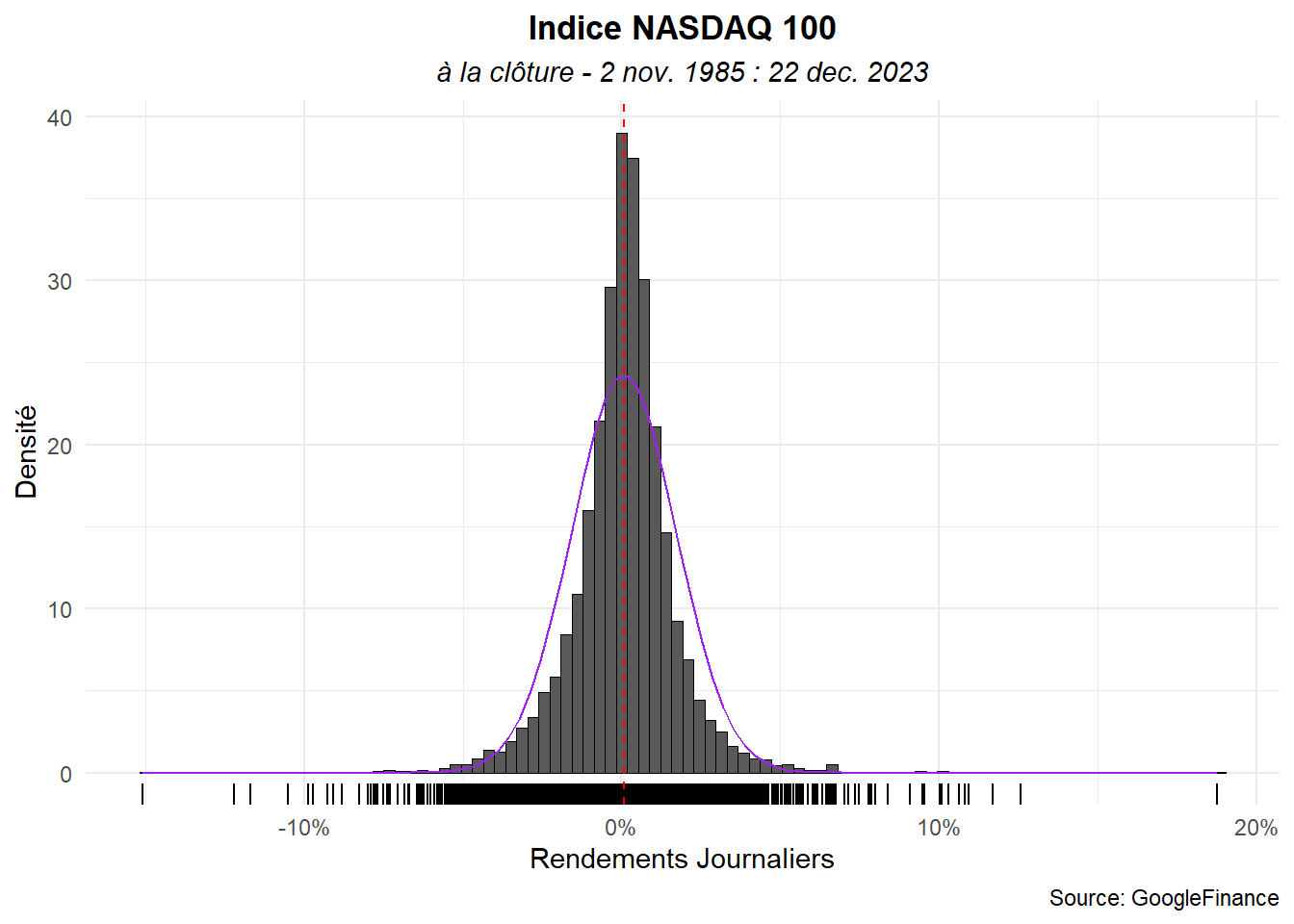
Ajoutons une étiquette pour la moyenne et une pour la distribution.
ggplot(data=dat_,aes(x=ret))+
geom_histogram(aes(y=after_stat(density)),
color='black',linewidth=0.001,
bins = 98)+
geom_rug()+
geom_vline(aes(xintercept = mean(ret)),
color='red',linetype = "dashed")+
stat_function(fun=dnorm,
args=list(mean(dat_$ret),sd(dat_$ret)),
color='purple')+
geom_text(aes(x=0.045,y=35,
label=paste("moyenne:",
round(mean(ret)*100,digits=2),"%")),
color="red",size=3)+
geom_text(aes(x=0.055,y=20,
label="distribution normale"),
color="purple",size=3)+
labs(title="Indice NASDAQ 100",
subtitle="à la clôture - 2 nov. 1985 : 22 dec. 2023",
caption="Source: GoogleFinance",
x="Rendements Journaliers",
y="Densité")+
scale_x_continuous(labels = label_percent())+
theme_minimal()+
theme(
plot.title = element_text(hjust=0.5,face='bold'),
plot.subtitle = element_text(hjust=0.5,face='italic')
)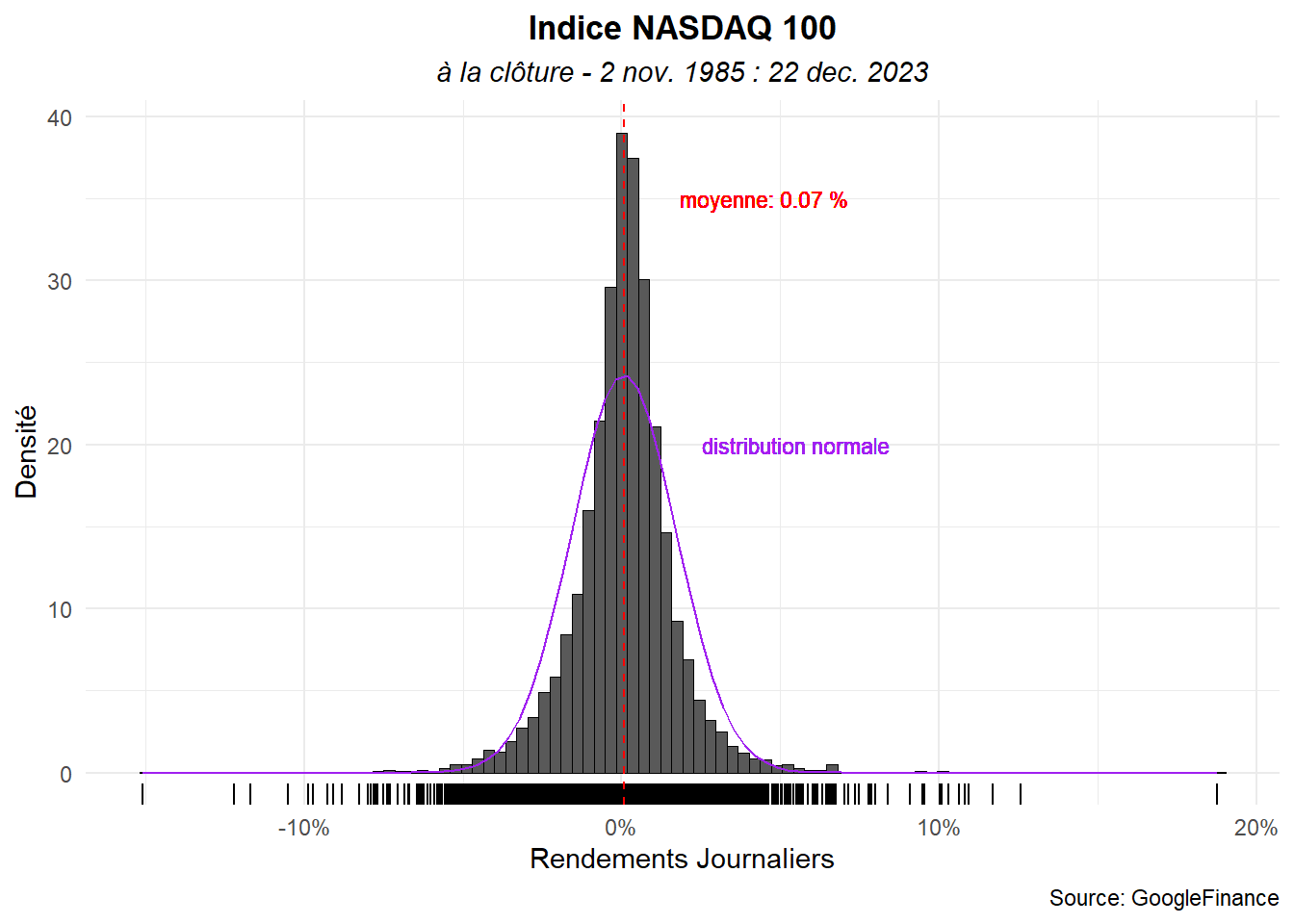
Retenons ce graphe. Créons une fonction permettant de le reproduire sur d’autres données sans les étiquettes.
hist_<-function(df,x,bi=100,
tit="",subt="",cap="",x_lab=""){
attach(df)
esp<-mean(x)
et<-sd(x)
detach()
g1<-ggplot(data=df,aes(x=x))+
geom_histogram(aes(y=after_stat(density)),
color='black',linewidth=0.001,
bins = bi)+
geom_vline(aes(xintercept = esp),
color='red',linetype = "dashed")+
geom_rug()+
stat_function(fun=dnorm,
args=list(esp,et),
color='purple')+
labs(title=tit,
subtitle=subt,
caption=cap,
x=x_lab,
y="Densité")+
scale_x_continuous(labels = label_percent())+
scale_y_continuous(labels = label_percent(scale=1))+
theme_minimal()+
theme(
plot.title = element_text(hjust=0.5,face='bold'),
plot.subtitle = element_text(hjust=0.5,face='italic')
)
return(g1)
}Voyons cela. Établissons cette fois les rendements sur une base hebdomadaires. Utilisons la fonction yearweek() du package tsibble.
dat_h<-dat %>%
mutate(yw=yearweek(date,week_start = 1)) %>%
group_by(yw) %>%
reframe(n=row_number(),
yw=yw,close=close) %>%
filter(n==1) %>%
select(-n) %>%
mutate(ret_h=close/lag(close)-1,
ret_c_h=log(close/lag(close))) %>%
drop_na()Avant d’établir le graphe, calculons le nombre d’intervalles à retenir avec la dernière méthode abordée (la racine carré du nombre d’observations ici 45). Plaçons également les annotations.
hist_(dat_h,ret_h,bi=45,
x_lab="Rendements Hebdomadaires",
tit="Indice NASDAQ 100",
sub="à la clôture - 2 nov. 1985 : 22 dec. 2023",
cap="Source: GoogleFinance")+
geom_text(aes(x=0.08,y=12,
label=paste("moyenne:",
round(mean(ret_h)*100,digits=2),"%")),
color="red",size=3)+
geom_text(aes(x=0.1,y=5,
label="distribution normale"),
color="purple",size=3)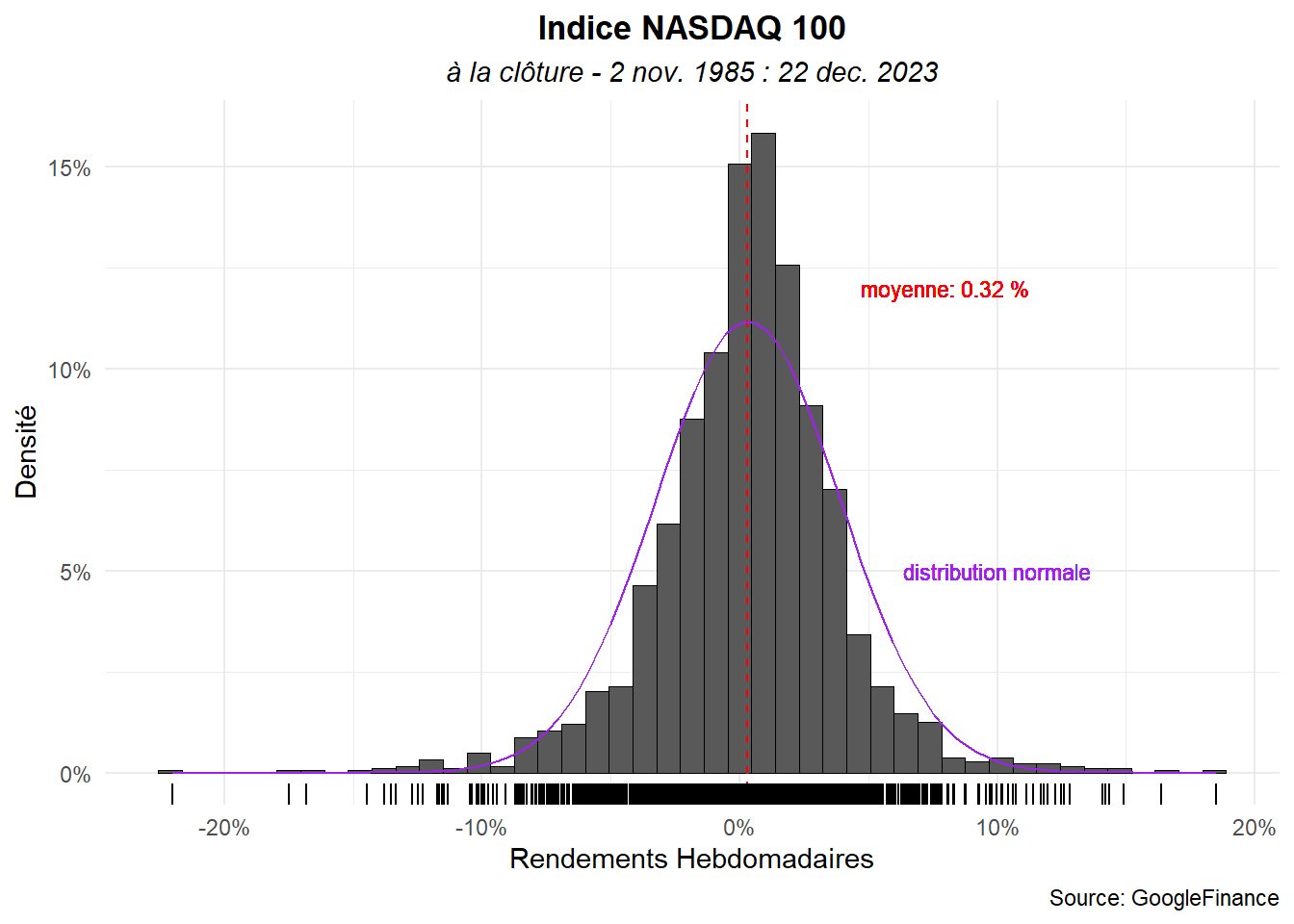
Voyons sur le même modèle les rendements mensuels.
dat_m<-dat %>%
mutate(ym=yearmonth(date)) %>%
group_by(ym) %>%
reframe(n=row_number(),
ym=ym,close=close) %>%
filter(n==1) %>%
select(-n) %>%
mutate(ret_m=close/lag(close)-1,
ret_c_m=log(close/lag(close))) %>%
drop_na()
summary(dat_m$ret_m)## Min. 1st Qu. Median Mean 3rd Qu. Max.
## -0.27424 -0.02357 0.01430 0.01344 0.05170 0.26535Établissons l’histogramme sur le même modèle que précédemment.
hist_(dat_m,ret_m,bi=22,
x_lab="Rendements Mensuels",
tit="Indice NASDAQ 100",
sub="à la clôture - 2 nov. 1985 : 22 dec. 2023",
cap="Source: GoogleFinance")+
geom_text(aes(x=0.08,y=8,
label=paste("moyenne:",
round(mean(ret_m)*100,digits=2),"%")),
color="red",size=3)+
geom_text(aes(x=0.15,y=5,
label="distribution normale"),
color="purple",size=3)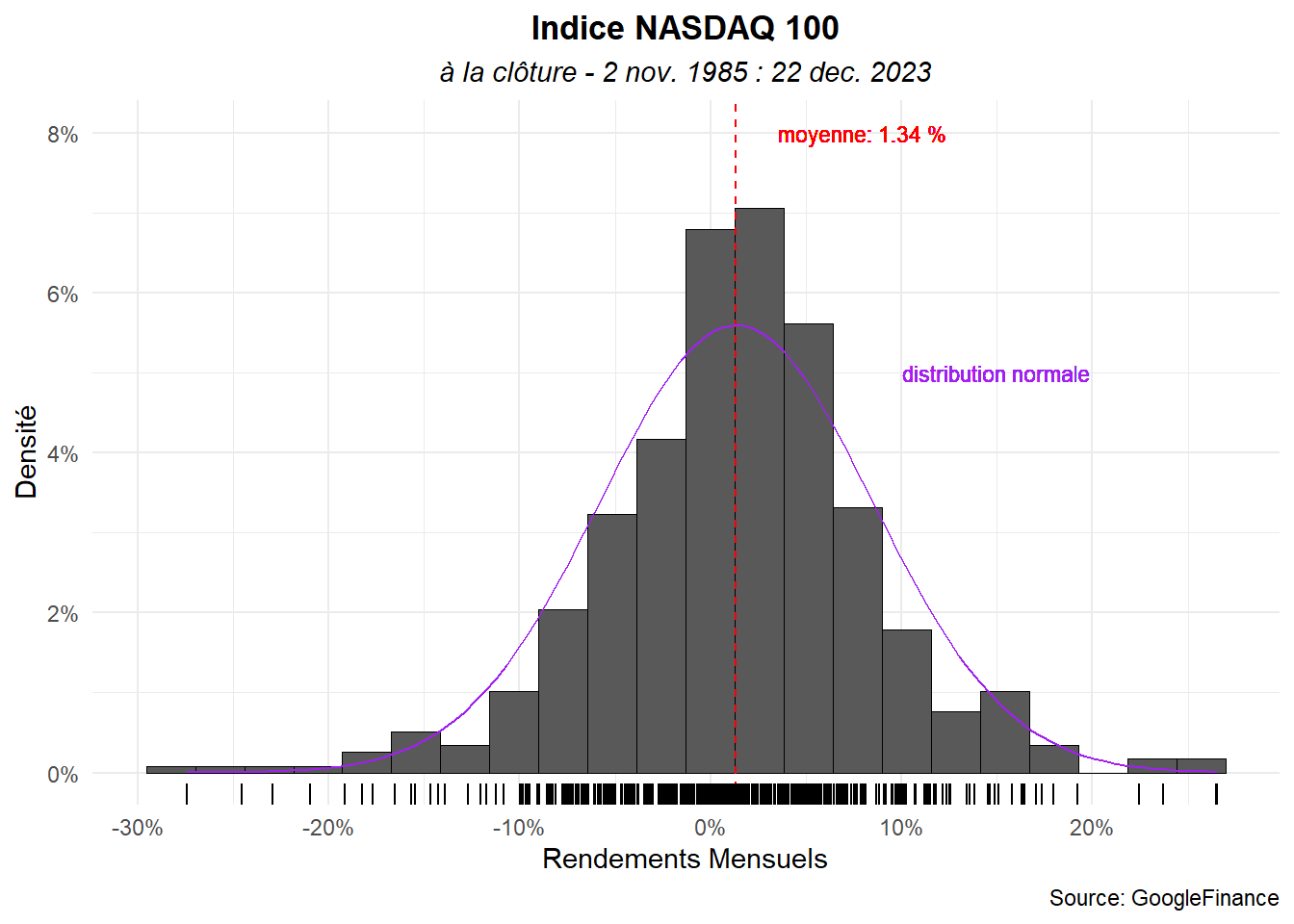
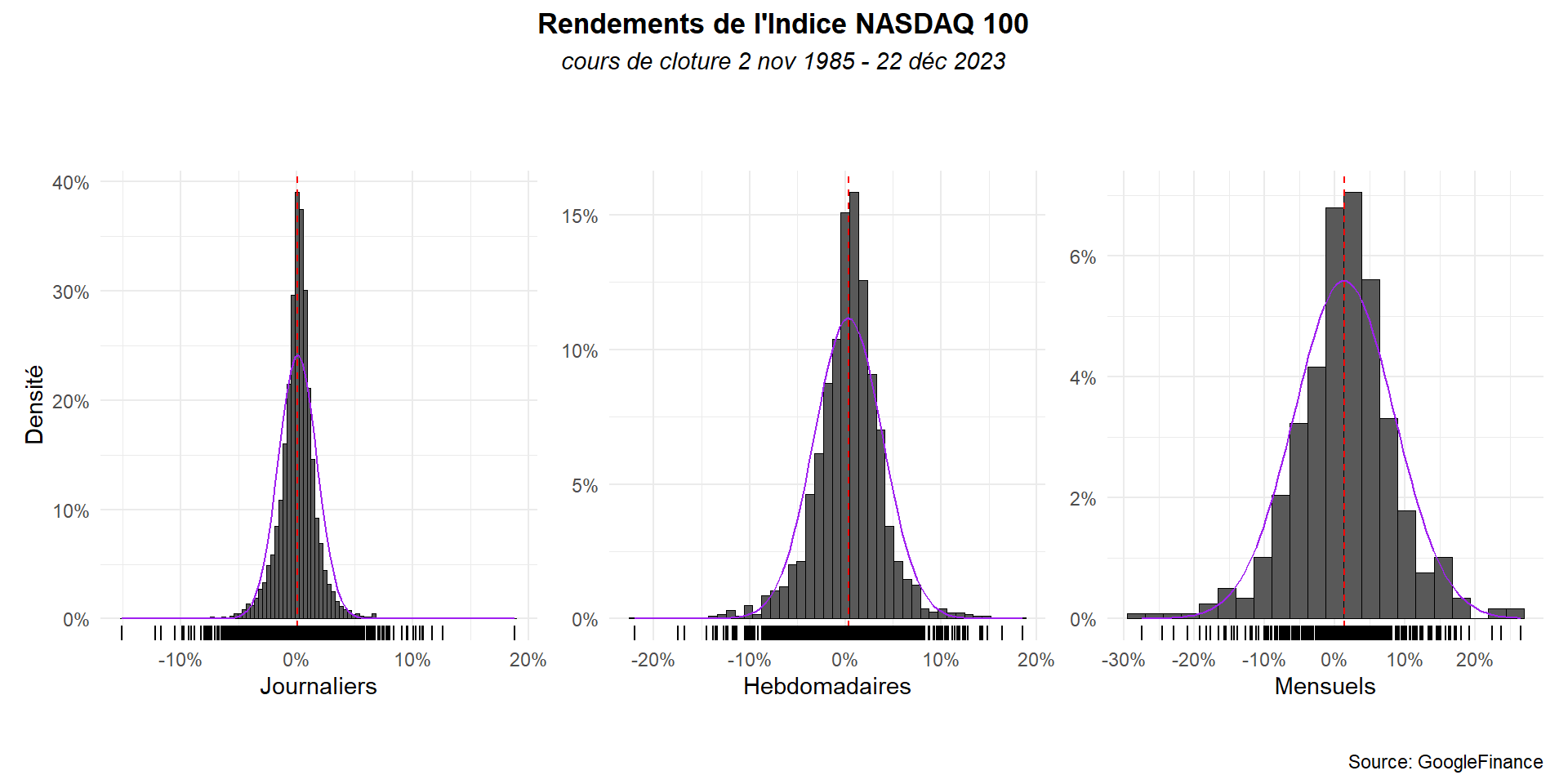
Pour mieux les comparer, mettons les trois graphes en vis-à-vis.
g1<-hist_(dat_,ret,bi=98,x_lab="Journaliers")
g2<-hist_(dat_h,ret_h,bi=45,x_lab="Hebdomadaires")+
theme(axis.title.y = element_blank())
g3<-hist_(dat_m,ret_m,bi=22,x_lab="Mensuels")+
theme(axis.title.y = element_blank())
g1+g2+g3+ plot_annotation(
title = "Rendements de l'Indice NASDAQ 100",
subtitle = 'cours de cloture 2 nov 1985 - 22 déc 2023',
caption = 'Source: GoogleFinance')&
theme(
plot.title = element_text(hjus=.5,face='bold'),
plot.subtitle = element_text(hjus=.5,face='italic')
)
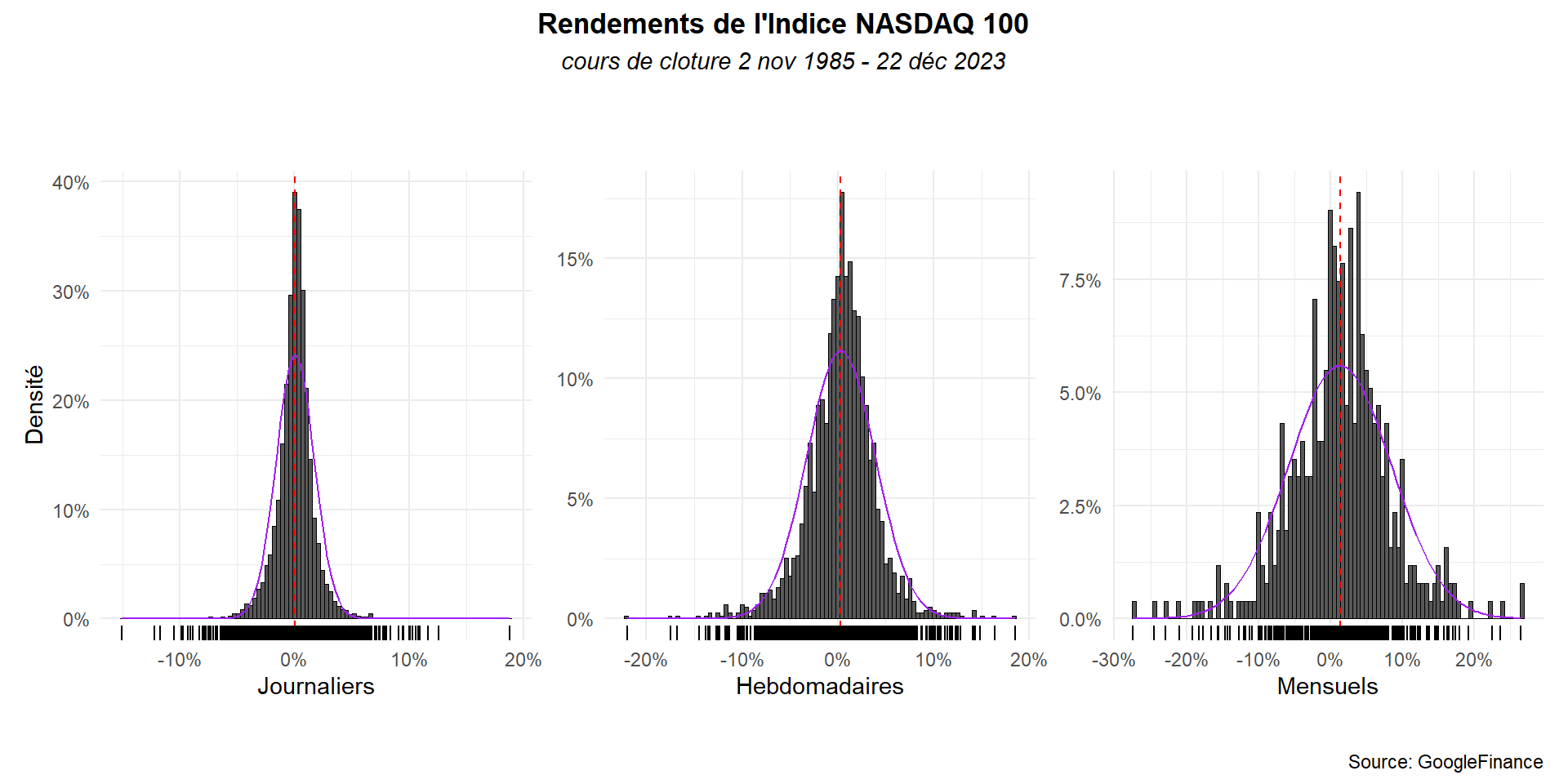
Passons l’ensemble des graphes à 98 intervalles.
g1<-hist_(dat_,ret,bi=98,x_lab="Journaliers")
g2<-hist_(dat_h,ret_h,bi=98,x_lab="Hebdomadaires")+
theme(axis.title.y = element_blank())
g3<-hist_(dat_m,ret_m,bi=98,x_lab="Mensuels")+
theme(axis.title.y = element_blank())
g1+g2+g3+ plot_annotation(
title = "Rendements de l'Indice NASDAQ 100",
subtitle = 'cours de cloture 2 nov 1985 - 22 déc 2023',
caption = 'Source: GoogleFinance')&
theme(
plot.title = element_text(hjus=.5,face='bold'),
plot.subtitle = element_text(hjus=.5,face='italic')
)
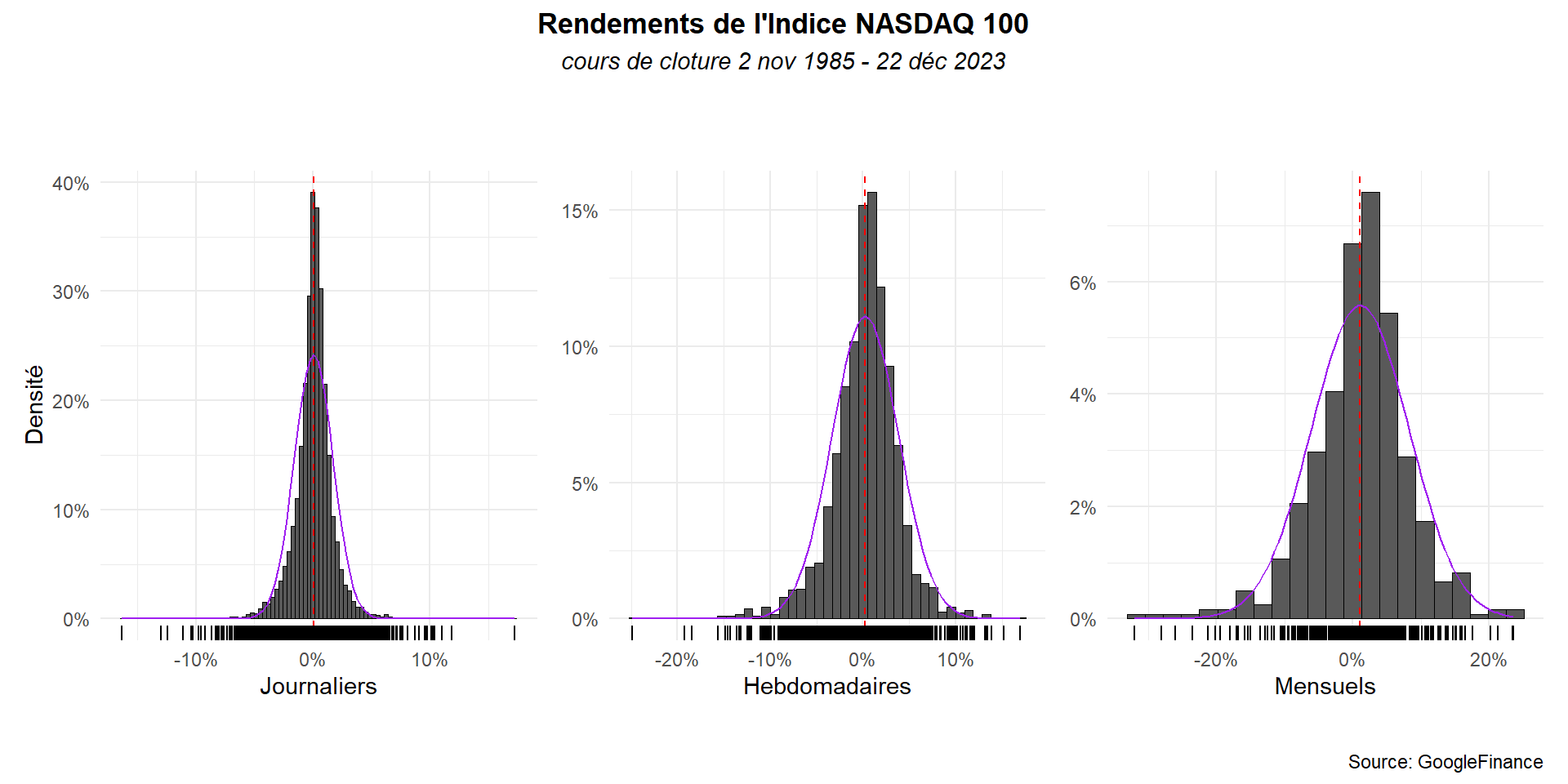
Voyons ce que les graphes donnes à partir des rendements continus.
g1<-hist_(dat_,ret_c,bi=98,x_lab="Journaliers")
g2<-hist_(dat_h,ret_c_h,bi=45,x_lab="Hebdomadaires")+
theme(axis.title.y = element_blank())
g3<-hist_(dat_m,ret_c_m,bi=22,x_lab="Mensuels")+
theme(axis.title.y = element_blank())
g1+g2+g3+ plot_annotation(
title = "Rendements de l'Indice NASDAQ 100",
subtitle = 'cours de cloture 2 nov 1985 - 22 déc 2023',
caption = 'Source: GoogleFinance')&
theme(
plot.title = element_text(hjus=.5,face='bold'),
plot.subtitle = element_text(hjus=.5,face='italic')
)
Voilà pour les histogrammes classiques. D’autres éléments de personnalisation pourrait être envisagés, nous y reviendrons à l’occasion.