Pour ce dernier post de la série consacrée au td de TQG, nous allons nous intéresser à ce qu’on appel l’effet lundi. Il s’agit de la propension qu’ont (qu’avaient?) les marchés actions à présenter des rendements moyens plus faibles les lundi que les autres jours de la semaine (Cross, 19731; French, 19802; Gibbons-Hess, 1981 3; et bien d’autres à la suite…). Le données utilisées sont issues de CRPS, une base qui a la particularité de conserver les titres éteins et donc de permettre d’éviter le biais du survivant (conclusion à tord parce que l’on observe qu’une partie de la réalité d’un phénomène, celle des seuls survivants). Elles concernent uniquement les titres côtés sur les marchés américains. Nous allons utiliser la régression linéaire sur variable binaire (dummy) pour test l’hypothèse de rendements différents des autres jours les lundi.
Pour commencer, comme à chaque fois, chargeons les packages que nous allons mobiliser.
library(tidyverse)
library(lubridate)Pour ce qui est des données, vous pouvez les télécharger ici. N’oubliez pas de les mettre dans votre dossier de travail. Cela facilite l’adressage pour l’importation des données dans R. Réalisons-la avec la fonction read_csv().
dat <- read_csv("monday_data.csv")## Rows: 24038 Columns: 8
## ── Column specification ────────────────────────────────────────────────────────
## Delimiter: ","
## dbl (8): YYYYMMDD, VWID, VWI, EWID, EWI, SP500, YYYY, day
##
## ℹ Use `spec()` to retrieve the full column specification for this data.
## ℹ Specify the column types or set `show_col_types = FALSE` to quiet this message.Ceci fait. On peut regarder ce que l’on a comme information. Utilisons-la fonction glimpse().
glimpse(dat)## Rows: 24,038
## Columns: 8
## $ YYYYMMDD <dbl> 19260102, 19260104, 19260105, 19260106, 19260107, 19260108, 1…
## $ VWID <dbl> 0.005689, 0.000706, -0.004821, -0.000423, 0.004988, -0.003238…
## $ VWI <dbl> 0.005689, 0.000706, -0.004867, -0.000427, 0.004953, -0.003549…
## $ EWID <dbl> 0.009516, 0.005780, -0.001927, 0.001182, 0.008453, -0.001689,…
## $ EWI <dbl> 0.009516, 0.005780, -0.002030, 0.001155, 0.008384, -0.001938,…
## $ SP500 <dbl> NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, N…
## $ YYYY <dbl> 1926, 1926, 1926, 1926, 1926, 1926, 1926, 1926, 1926, 1926, 1…
## $ day <dbl> 6, 1, 2, 3, 4, 5, 6, 1, 2, 3, 4, 5, 6, 1, 2, 3, 4, 5, 6, 1, 2…On a une indication de date (YYYMMDD), différents indices de marché, une variable année (YYYY) et une variable indiquant le jour de la semaine (day). L’ensemble est au format double.
Créons une variable exprimant la date dans un format compris comme une date. Pour cela, utilisons la fonction ymd() du package lubridate. A partir de cette nouvelle variable, nous pouvons créer la variable jours qui indique le jours de la semaine de la date considéré. Cela nous permettra de vérifier que la valeur 1 de day correspond bien au lundi. Pour cela, utilisons la fonction wday() (qui encore une fois est issue de lubridate).
dat<-dat %>% mutate(date=ymd(YYYYMMDD),
jours=wday(date,week_start=1,label=TRUE,abbr=FALSE))
head(dat)[,8:10]## # A tibble: 6 × 3
## day date jours
## <dbl> <date> <ord>
## 1 6 1926-01-02 samedi
## 2 1 1926-01-04 lundi
## 3 2 1926-01-05 mardi
## 4 3 1926-01-06 mercredi
## 5 4 1926-01-07 jeudi
## 6 5 1926-01-08 vendrediLa valeur 1 de day correspond bien au lundi. Codons une variable binaire prenant la valeur TRUE (1) si day égale 1 (lundi) et FALSE (0) dans le cas contraire. Appelons la Monday_bin.
dat <- dat %>% mutate(Monday_bin=day==1)Limitons nous pour la suite au premier indice présenté VWID (vous pouvez répliquer ce qui suit avec les autres. Cela peut être un bon exercice. Les résultat seront qualitativement les mêmes).
Commençons par une rapide représentation graphe des rendements de l’indice les lundi contre l’ensemble des autres jours. Marquons en rouge la moyenne globale des rendements et en bleu celle des seuls lundi et celle des autres jours.
ggplot(data=dat,aes(x=Monday_bin,y=VWID))+
geom_point()+
geom_hline(yintercept=mean(dat$VWID),color='red',
linetype='dashed')+
geom_point(aes(y=mean(filter(dat,Monday_bin==TRUE)$VWID),x=TRUE),
color='blue')+
geom_point(aes(y=mean(filter(dat,Monday_bin==FALSE)$VWID),x=FALSE),
color='blue')+
theme_minimal()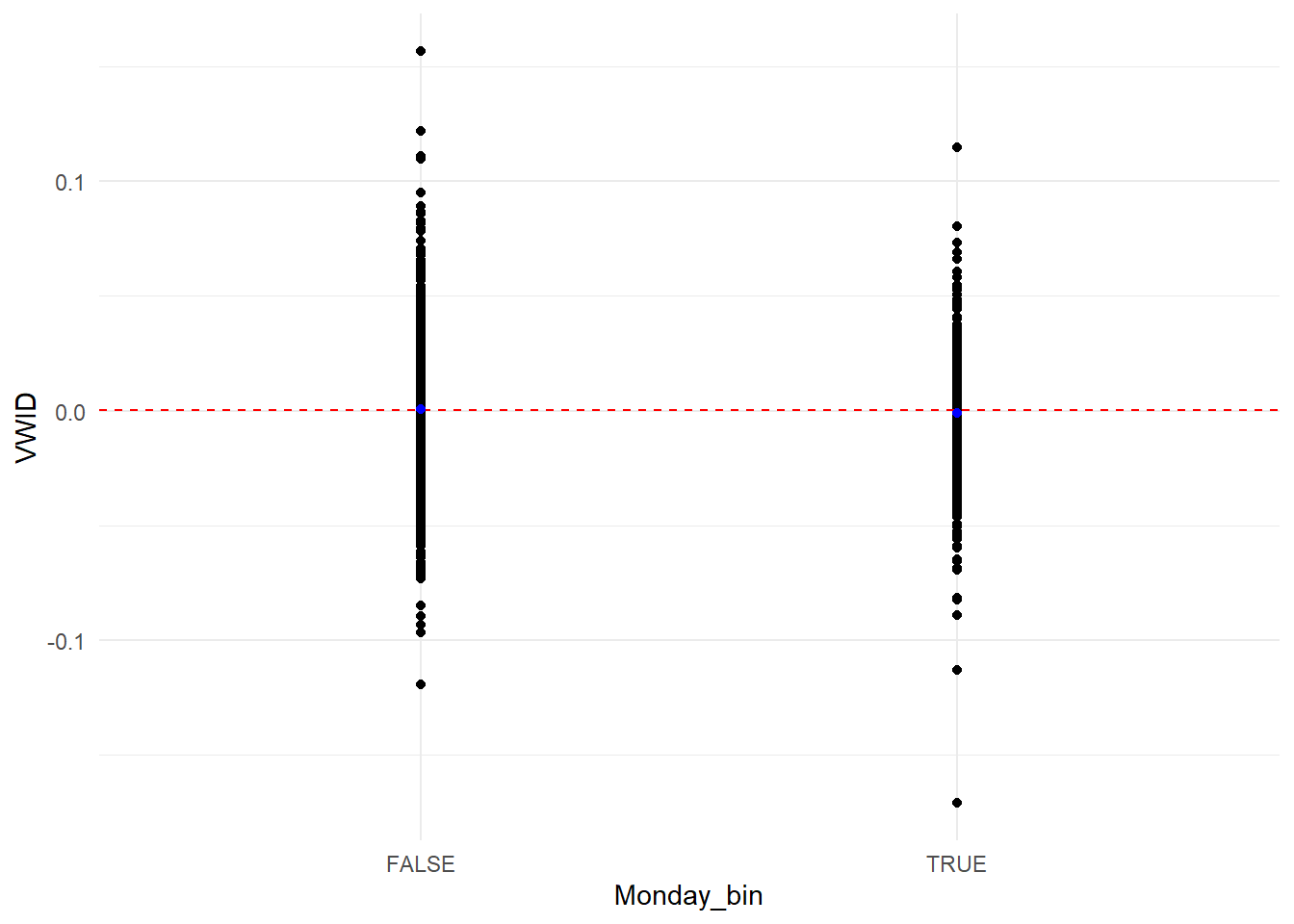
On peut voir que les deux distributions ne se superposent pas complément. Les rendements du lundi apparaissent légèrement plus petits que ceux des autres jours. Néanmoins, les choses peuvent être plus compliquées. Réalisons un test de différence de moyenne pour avoir une image plus nette.
round(data.frame(moy_tot=mean(dat$VWID),
moy_lundi=mean(filter(dat,Monday_bin==TRUE)$VWID),
moy_aut_jours=mean(filter(dat,Monday_bin==FALSE)$VWID),
t_stat=t.test(VWID~Monday_bin,data=dat)$statistic,
p_val=t.test(VWID~Monday_bin,data=dat)$p.value),
digits=7)## moy_tot moy_lundi moy_aut_jours t_stat p_val
## t 0.000407 -0.0010861 0.0007422 9.610673 0L’hypothèse H0 d’égalité des moyennes des rendements entre les lundi et les autres jours est clairement rejetée. Voyons si on aboutit à la même conclusion sur la base d’une régression simple.
reg_m<-lm(VWID~Monday_bin,data=dat)
summary(reg_m)##
## Call:
## lm(formula = VWID ~ Monday_bin, data = dat)
##
## Residuals:
## Min 1Q Median 3Q Max
## -0.170263 -0.004222 0.000327 0.004578 0.156096
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 7.422e-04 7.568e-05 9.808 <2e-16 ***
## Monday_binTRUE -1.828e-03 1.767e-04 -10.345 <2e-16 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 0.0106 on 24036 degrees of freedom
## Multiple R-squared: 0.004433, Adjusted R-squared: 0.004391
## F-statistic: 107 on 1 and 24036 DF, p-value: < 2.2e-16Le coefficient associé aux lundi est négatif et statistiquement significatif ce qui va dans le sens ce que l’on a vue avec le test de différence de moyennes (bon ce n’est pas une surprise mais…). On peut à partir du modèle sortir l’intervalle de confiance du coefficient avec confint().
confint(reg_m,parm=2,level=0.95)## 2.5 % 97.5 %
## Monday_binTRUE -0.002174795 -0.001481941Sur tout l’intervalle à 95%, le coefficient est négatif. Les rendements des lundi sont plus petits dans les rendements des autres jours.
On peut retrouver les moyennes des groupes à partir des coefficients de régression. On a ainsi:
round(data.frame(rend_aut_jr=coef(reg_m)[1] %>% unname(),
rend_lundi=sum(coef(reg_m))),
digits=7)## rend_aut_jr rend_lundi
## 1 0.0007422 -0.0010861Voyons maintenant si cet effet lundi est toujours présent aprés les années 90. Pour cela, commençons par créer une variable marquant les observations post 1990.
dat<-dat %>% mutate(post90=YYYY>=1990)Réalisons le test de différence de moyenne sur la base réduite.
dat_90<-filter(dat,post90==TRUE)
round(data.frame(moy_tot=mean(dat_90$VWID),
moy_lundi=mean(filter(dat_90,Monday_bin==TRUE)$VWID),
moy_aut_jours=
mean(filter(dat_90,Monday_bin==FALSE)$VWID),
t_stat=t.test(VWID~Monday_bin,data=dat_90)$statistic,
p_val=t.test(VWID~Monday_bin,data=dat_90)$p.value),
digits=7)## moy_tot moy_lundi moy_aut_jours t_stat p_val
## t 0.0004143 0.00015 0.0004758 0.8800766 0.3789364La différence entre les deux moyennes n’est plus statistiquement significative. La p value du test est trop élevée pour que l’on rejette H0 (égalité des moyennes) à un niveau de confiance raisonnable (90%,95%,99%).
Cette absence de différence se voit bien sur le graphe du nuage de points des rendements sur les deux groupes d’observations (lundi vs autres jours).
ggplot(data=dat_90,aes(x=Monday_bin,y=VWID))+
geom_point()+
geom_hline(yintercept=mean(dat_90$VWID),color='red',linetype='dashed')+
geom_point(aes(y=mean(filter(dat_90,Monday_bin==TRUE)$VWID),x=TRUE),
color='blue')+
geom_point(aes(y=mean(filter(dat_90,Monday_bin==FALSE)$VWID),x=FALSE),
color='blue')+
theme_minimal()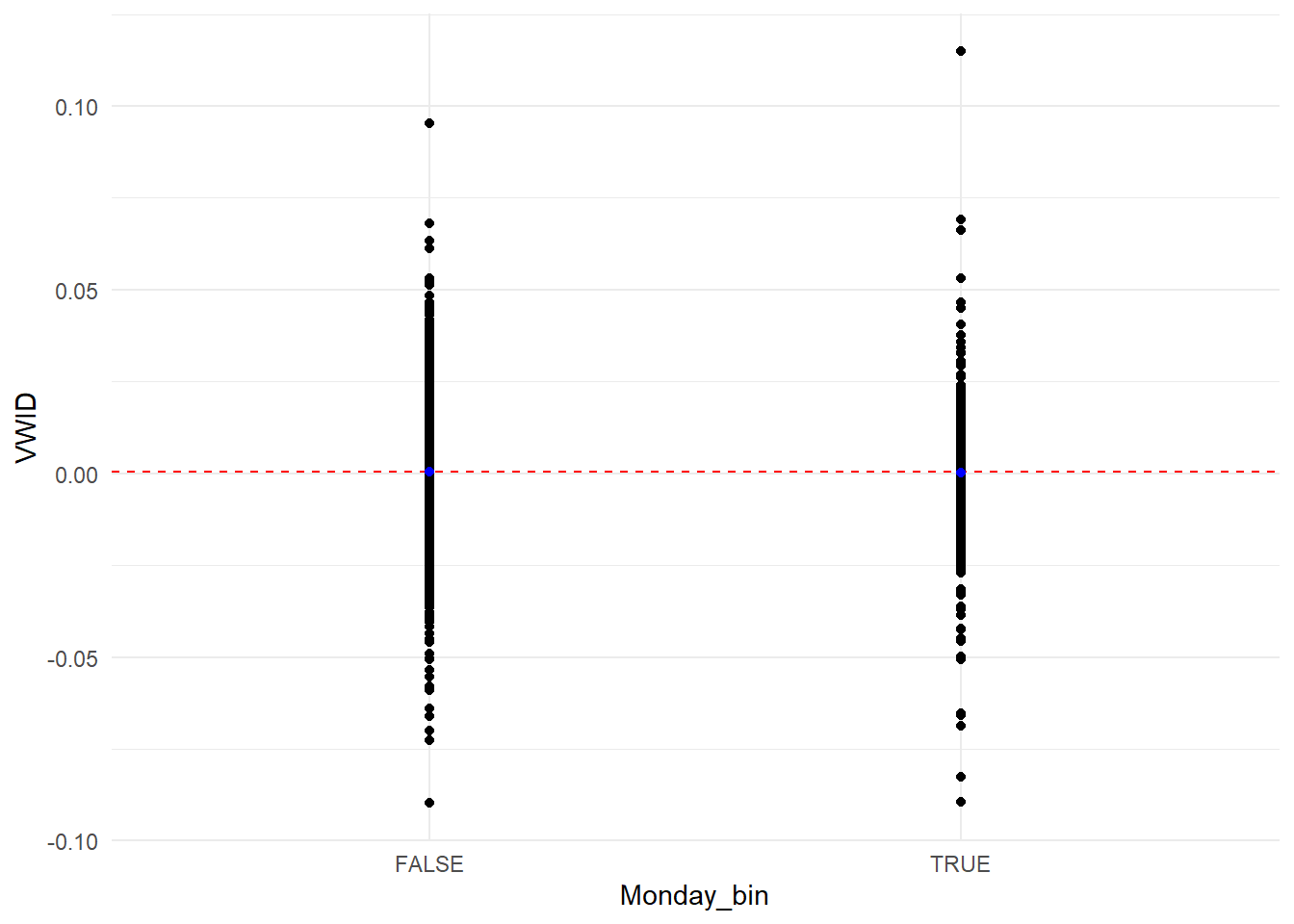
Réalisons à nouveau le test au travers d’une régression simple.
reg_m90<-lm(VWID~Monday_bin,data=dat_90)
summary(reg_m90)##
## Call:
## lm(formula = VWID ~ Monday_bin, data = dat_90)
##
## Residuals:
## Min 1Q Median 3Q Max
## -0.090247 -0.004771 0.000331 0.005143 0.114737
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 0.0004758 0.0001492 3.189 0.00144 **
## Monday_binTRUE -0.0003259 0.0003433 -0.949 0.34248
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 0.01109 on 6803 degrees of freedom
## Multiple R-squared: 0.0001325, Adjusted R-squared: -1.452e-05
## F-statistic: 0.9012 on 1 and 6803 DF, p-value: 0.3425Le coefficient de la variable marquant les lundi n’est pas significativement différent de zéro. L’effet lundi ne semble plus être présent après 1990.
Encore une fois, on peut retrouver les moyennes des groupes à partir des coefficients de la régression.
round(data.frame(rend_aut_jr=coef(reg_m90)[1] %>% unname(),
rend_lundi=sum(coef(reg_m90))),
digits=7)## rend_aut_jr rend_lundi
## 1 0.0004758 0.00015Une autre façon de procéder pourrait consister à régresser l’interaction entre la variable marquant les lundi et celle marquant la période post 1990.
reg_m90alt<-lm(VWID~Monday_bin*post90,data=dat)
summary(reg_m90alt)##
## Call:
## lm(formula = VWID ~ Monday_bin * post90, data = dat)
##
## Residuals:
## Min 1Q Median 3Q Max
## -0.169754 -0.004230 0.000303 0.004595 0.155992
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 8.464e-04 8.921e-05 9.488 < 2e-16 ***
## Monday_binTRUE -2.442e-03 2.096e-04 -11.649 < 2e-16 ***
## post90TRUE -3.706e-04 1.682e-04 -2.203 0.0276 *
## Monday_binTRUE:post90TRUE 2.116e-03 3.894e-04 5.434 5.55e-08 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 0.0106 on 24034 degrees of freedom
## Multiple R-squared: 0.005655, Adjusted R-squared: 0.005531
## F-statistic: 45.57 on 3 and 24034 DF, p-value: < 2.2e-16On obtient trois coefficients en plus de la constante. On peut à partir de ces indications retrouver les moyennes des rendements sur les groupes d’observations constitué à partir à partir des deux variables.
round(data.frame(
aut_jrs_avant90=coef(reg_m90alt)[1] %>% unname(),
lundi_avant90=sum(coef(reg_m90alt)[1:2]),
aut_jrs_post90=sum(coef(reg_m90alt)[c(1,3)]),
lundi_post90=sum(coef(reg_m90alt))),digits=7)## aut_jrs_avant90 lundi_avant90 aut_jrs_post90 lundi_post90
## 1 0.0008464 -0.0015955 0.0004758 0.00015Un des résultats important pour la compréhension du phénomène mis en évidence par la littérature (voir Doyle et Chen, 20094) est que l’intensité de celui-ci serait lié à la performance des marchés la semaine précédent le lundi considéré. Testons nous-même cette hypothèse. Introduisons dans notre base générale une variable reflétant sur les lundi la performance sur la semaine précédente (il s’agit d’une variable d’interaction Monday_bin et performance sur la semaine précédente).
dat_twi<-dat %>% select(VWID,date,YYYY,jours,Monday_bin) %>%
arrange(date) %>%
mutate(week=week(date-2)) %>%
group_by(YYYY,week) %>%
mutate(moy_we_r=mean(VWID)) %>%
ungroup() %>%
mutate(monday_perf_l=Monday_bin*lag(moy_we_r))Régression les performances de l’indice sur la variable lundi et notre nouvelle variable (d’intéraction). Si la performance sur la semaine précédente guide la performe du lundi, le coefficient de la nouvelle variable devrait être positif.
reg_m_tw<-lm(VWID~Monday_bin+monday_perf_l,data=dat_twi)
summary(reg_m_tw)##
## Call:
## lm(formula = VWID ~ Monday_bin + monday_perf_l, data = dat_twi)
##
## Residuals:
## Min 1Q Median 3Q Max
## -0.154422 -0.004233 0.000259 0.004488 0.156096
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 7.420e-04 7.457e-05 9.95 <2e-16 ***
## Monday_binTRUE -2.201e-03 1.747e-04 -12.60 <2e-16 ***
## monday_perf_l 8.843e-01 3.295e-02 26.84 <2e-16 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 0.01045 on 24034 degrees of freedom
## (1 observation effacée parce que manquante)
## Multiple R-squared: 0.0334, Adjusted R-squared: 0.03332
## F-statistic: 415.3 on 2 and 24034 DF, p-value: < 2.2e-16Le coefficient de la variable d’intéraction est positif et statistiquement significatif. Il apparaît que l’effet lundi est bien corrélé avec la performance de la semaine précédente. Pour illustrer l’ensemble retrouvons les moyennes à partir des coefficients. Commençons par calculer la performance moyenne des semaines précédentes.
moy_perf_l<-mean(dat_twi$monday_perf_l[dat_twi$monday_perf_l!=0],
na.rm=TRUE)Appliquons nos coefficients pour obtenir nos performances.
round(data.frame(
aut_jrs=coef(reg_m_tw)[1] %>% unname(),
lundi_perf0=sum(coef(reg_m_tw)[1:2]),
lundi_perfM=
sum(coef(reg_m_tw)[1:2])+unname(coef(reg_m_tw)[3]*moy_perf_l)),
digits=7)## aut_jrs lundi_perf0 lundi_perfM
## 1 0.000742 -0.0014592 -0.0010861Voyons si le lien perdure après 1990.
reg_m_twr<-lm(VWID~Monday_bin+monday_perf_l,
data=filter(dat_twi,YYYY>=1990))
summary(reg_m_twr)##
## Call:
## lm(formula = VWID ~ Monday_bin + monday_perf_l, data = filter(dat_twi,
## YYYY >= 1990))
##
## Residuals:
## Min 1Q Median 3Q Max
## -0.090247 -0.004889 0.000316 0.005115 0.123810
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 0.0004758 0.0001481 3.212 0.00132 **
## Monday_binTRUE -0.0006235 0.0003421 -1.823 0.06837 .
## monday_perf_l 0.6382785 0.0635539 10.043 < 2e-16 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 0.01101 on 6802 degrees of freedom
## Multiple R-squared: 0.01474, Adjusted R-squared: 0.01445
## F-statistic: 50.89 on 2 and 6802 DF, p-value: < 2.2e-16Recalculons la performance moyenne des semaines précédentes sur l’échantillon limité à la période post 1990.
moy_perf_lr<-mean(filter(dat_twi,
YYYY>=1990)$monday_perf_l[dat_twi$monday_perf_l!=0],
na.rm=TRUE)Cela nous permet de ré-estimer les performances moyennes pour les groupes désignés.
round(data.frame(
aut_jrs=coef(reg_m_twr)[1] %>% unname(),
lundi_perf0=sum(coef(reg_m_twr)[1:2]),
lundi_perfM=
sum(coef(reg_m_twr)[1:2])+unname(coef(reg_m_twr)[3]*moy_perf_lr)),
digits=7)## aut_jrs lundi_perf0 lundi_perfM
## 1 0.0004758 -0.0001477 -0.0001786Je vous laisse interpréter ces nouveaux éléments… Et, aux étudiants qui par hasard auraient lu cette série de post, je souhaites bonne chance pour l’examen.
Cross, F., 1973, The behavior of stock prices on Fridays and Mondays, Financial Analysts Journal, 29, Nov.-Dec., 67-69.↩︎
French, K., 1980, Stock returns and the weekend effect, Journal of Financial Economics, 8, March, 55-69.↩︎
Gibbons, M. and P. Hess, 1981, Day of the week effects and asset returns, Journal of Business, 54, Oct., 579-596.↩︎
Doyle, J. and C. Chen, 2009, The wandering weekday effect in major stock markets, Journal of Banking and Finance, 33, 1388-1399.↩︎