Entamer l’écriture un nouveau papier est l’occasion de revenir sur des méthodes que j’ai déjà utiliser et d’en découvrir de nouvelles. J’en profites pour réviser et partager quelques réflexions techniques. Il s’agit de travailler des données des panels. Bon rien d’original ici. La grande majorité de mes travaux utilisent ce type d’informations notamment au travers de modèles à effets fixes. Le défaut de la méthode est qu’elle nécessite que l’ensemble des informations traitées varies à la fois entre les individus et dans le temps. Une solution que je viens de découvrir au fil des lectures pour mobiliser en complément des variables fixes dans l’analyse est de passer par des modèles hybrides de type between-within. Ceux-ci sont développés par Allison (2009) et Bell et Jones (2015). Mais avant d’entamer leur analyse, débutons une série de postes pour revenir sur quelques basiques concernant les données des panels.
Pour commencer, chargeons quelques packages: le tidyverse, broom, qui permet de gérer les estimations de modèle comme des tibbles, plm, qui permet d’estimer les modèles de panel classiques, et panelr, qui permet notamment d’estimer les modèles hybrides.
library(tidyverse)
library(broom)
library(plm)
library(panelr)
library(lmtest) Chargeons également un jeu de données afin de réaliser nos différentes expérimentations. Utilisons le jeu WageData qui est inclus dans panelr.
wages<-WageData
glimpse(wages)## Rows: 4,165
## Columns: 14
## $ exp <dbl> 3, 4, 5, 6, 7, 8, 9, 30, 31, 32, 33, 34, 35, 36, 6, 7, 8, 9, 10,…
## $ wks <dbl> 32, 43, 40, 39, 42, 35, 32, 34, 27, 33, 30, 30, 37, 30, 50, 51, …
## $ occ <dbl> 0, 0, 0, 0, 0, 0, 0, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1…
## $ ind <dbl> 0, 0, 0, 0, 1, 1, 1, 0, 0, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 0…
## $ south <dbl> 1, 1, 1, 1, 1, 1, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0…
## $ smsa <dbl> 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1…
## $ ms <dbl> 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 0, 0, 0…
## $ fem <dbl> 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1…
## $ union <dbl> 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 1, 1, 1, 1, 1, 1, 1, 0…
## $ ed <dbl> 9, 9, 9, 9, 9, 9, 9, 11, 11, 11, 11, 11, 11, 11, 12, 12, 12, 12,…
## $ blk <dbl> 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1…
## $ lwage <dbl> 5.56068, 5.72031, 5.99645, 5.99645, 6.06146, 6.17379, 6.24417, 6…
## $ t <dbl> 1, 2, 3, 4, 5, 6, 7, 1, 2, 3, 4, 5, 6, 7, 1, 2, 3, 4, 5, 6, 7, 1…
## $ id <dbl> 1, 1, 1, 1, 1, 1, 1, 2, 2, 2, 2, 2, 2, 2, 3, 3, 3, 3, 3, 3, 3, 4…La base comprend 4 165 observations sur 14 variables. Deux d’entre-elles structurent l’ensemble id, identifiant des individus sur lesquels l’information est collectée, et t, qui marque la date de cette collecte.
paste('On a',length(unique(wages$id)),'individus')## [1] "On a 595 individus"paste('observés sur',length(unique(wages$t)),'périodes')## [1] "observés sur 7 périodes"paste('soit',595*7,'observations')## [1] "soit 4165 observations"Le panel est cylindré. La variable que l’on va expliquer ici est lwage, le log du salaire sur la période. Elle sera reprise par la suite comme yit. Voyons à quoi ressemble sa distribution.
wages %>%
summarise(min_=min(lwage),
Prem_Q=quantile(lwage,probs=0.25),
median_=median(lwage),
Trois_Q=quantile(lwage,probs=0.75),
max_=max(lwage),
mean_=mean(lwage),
sd_=sd(lwage))## min_ Prem_Q median_ Trois_Q max_ mean_ sd_
## 1 4.60517 6.39526 6.68461 6.95273 8.537 6.676346 0.4615122On a quelque chose proche d’une loi normale. L’hétérogénéité des situations est ici marquée par l’écart type. Cette hétérogénéité a deux sources : la variation des situations individuelles au travers le temps (variance intra-individuelle) et les différences de situations individuelles indépendantes du temps (variance inter-individuelle).
Pour s’en donner une idée, présentons deux graphes s’organisant sur le même principe. On présente la moyenne de la variable expliquée (lwage) et son intervalle de confiance à 95% calculés en fonction du découpage suivi. Pour la premier, consacré à la variation intra-individuelle, le calcule s’opère pour tout les individus (595) sur chaque période.
het_gr <- function(df, var1, var2, titre,mx_){
var1 <- enquo(var1); var2 <- enquo(var2);
df_<-df %>% group_by(!!var1) %>%
summarise(mean_=mean(!!var2),
bas=t.test(!!var2)$conf.int[1],
haut=t.test(!!var2)$conf.int[2],
)
ggplot(data=df_,aes(x=!!var1))+
geom_point(aes(y=mean_),color='red')+
geom_line(aes(y=mean_),color='red',size=0.5)+
geom_segment(aes(xend=!!var1,x=!!var1,yend=haut,y=bas))+
labs(title=titre)+
scale_x_continuous(breaks=mx_)+
theme_minimal()+
theme(plot.title = element_text(hjust=0.5))}
het_gr (df = wages, var1 = t, var2 = lwage,
titre='Hétérogénéité entre les périodes',mx_=1:7)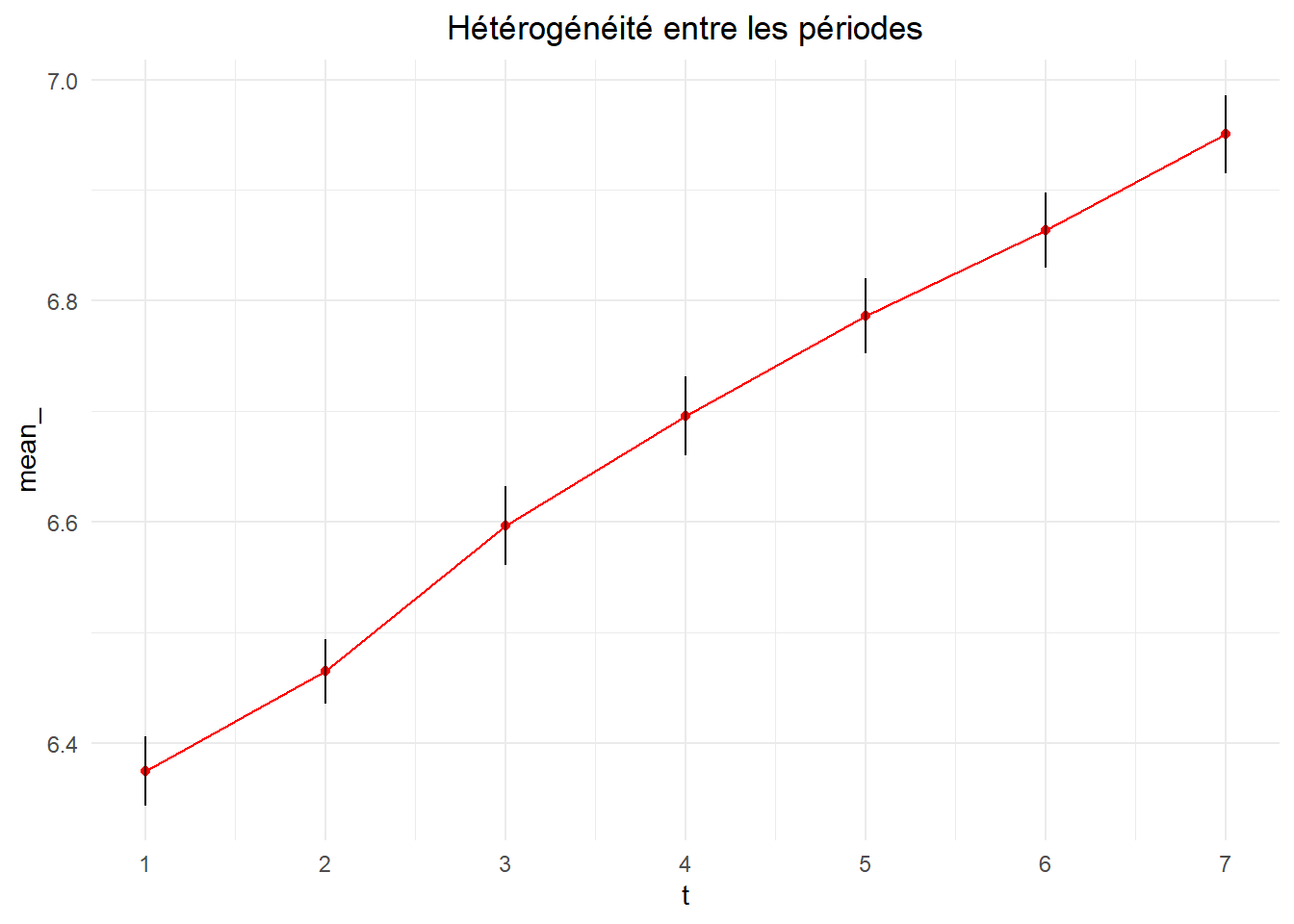
On voit ici une nette tendance haussière des salaires sur la période d’étude. Le second graphe s’établit sur une base individuel. Les calculs sont fait sur chaque individu (id) pour la période d’étude (7).
het_gr (df = wages, var1 = id, var2 = lwage,
titre='Hétérogénéité entre les individus',mx_=seq(0,600,50))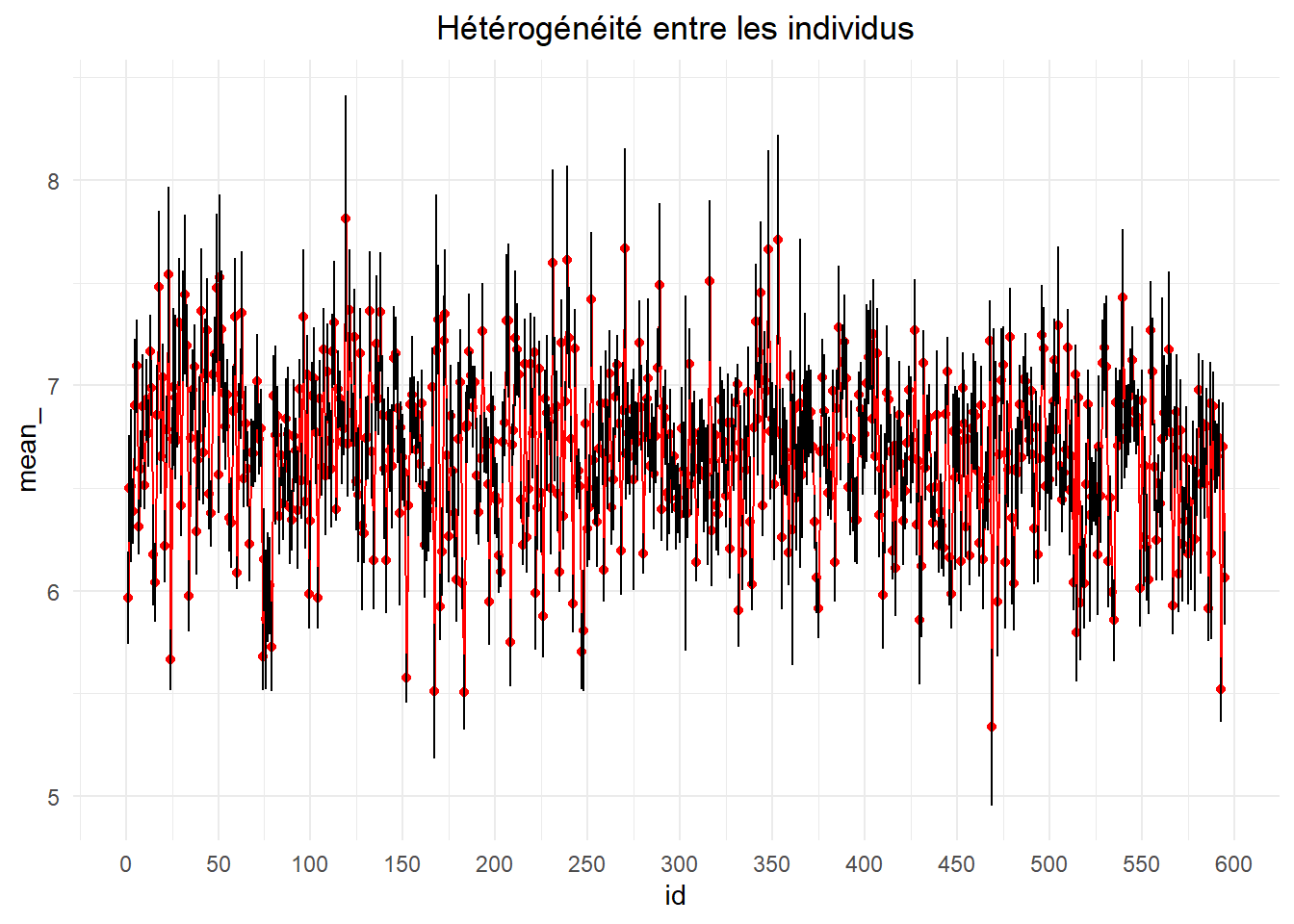
L’ordre des individus est celui de leur identifiant. Celui-ci est assigné de manière aléatoire. Il n’y a donc pas de tendance qui se dégage. On peut néanmoins observer la variabilité inter-individuelle.
Ceci étant observé, intéressons-nous à la manière dont le nombre de semaines travaillées (wks) influence le salaire (lwage). Cette variable explicative sera nommée de manière générale xit. Le premier réflexe que l’on a souvent est d’ignorer la décomposition de l’hétérogéniété et d’estimer simplement un modèle linéaire classique.
yit=α+β1.xit+uit
Ce type de modèle utilisé sur de données de panel est appelé modèle de pooling. Estimons-le avec la fonction lm().
lm(lwage~wks,data=wages) %>% tidy() ## # A tibble: 2 × 5
## term estimate std.error statistic p.value
## <chr> <dbl> <dbl> <dbl> <dbl>
## 1 (Intercept) 6.43 0.0656 98.1 0
## 2 wks 0.00527 0.00139 3.78 0.000157Le même résultat est obtenu avec la fonction plm() du package du même nom. Précisons y les variables indexant les individus et les périodes.
g <- plm(lwage ~ wks, data=wages, index=c("id"),model="pooling")
g %>% tidy()## # A tibble: 2 × 5
## term estimate std.error statistic p.value
## <chr> <dbl> <dbl> <dbl> <dbl>
## 1 (Intercept) 6.43 0.0656 98.1 0
## 2 wks 0.00527 0.00139 3.78 0.000157Quel que soient la fonction d’estimation utilisée, il s’agit de résumer l’information contenu dans le nuage de points (noirs) à partir de la droite (en rouge) dont nous venons trouver les paramètres.
ggplot(data=wages,aes(x=wks,y=lwage))+
geom_point()+
geom_smooth(method = "lm",color='red',se=FALSE)+
coord_cartesian(expand=FALSE,xlim=c(4,53),ylim=c(4.5,8.7))+
theme_minimal()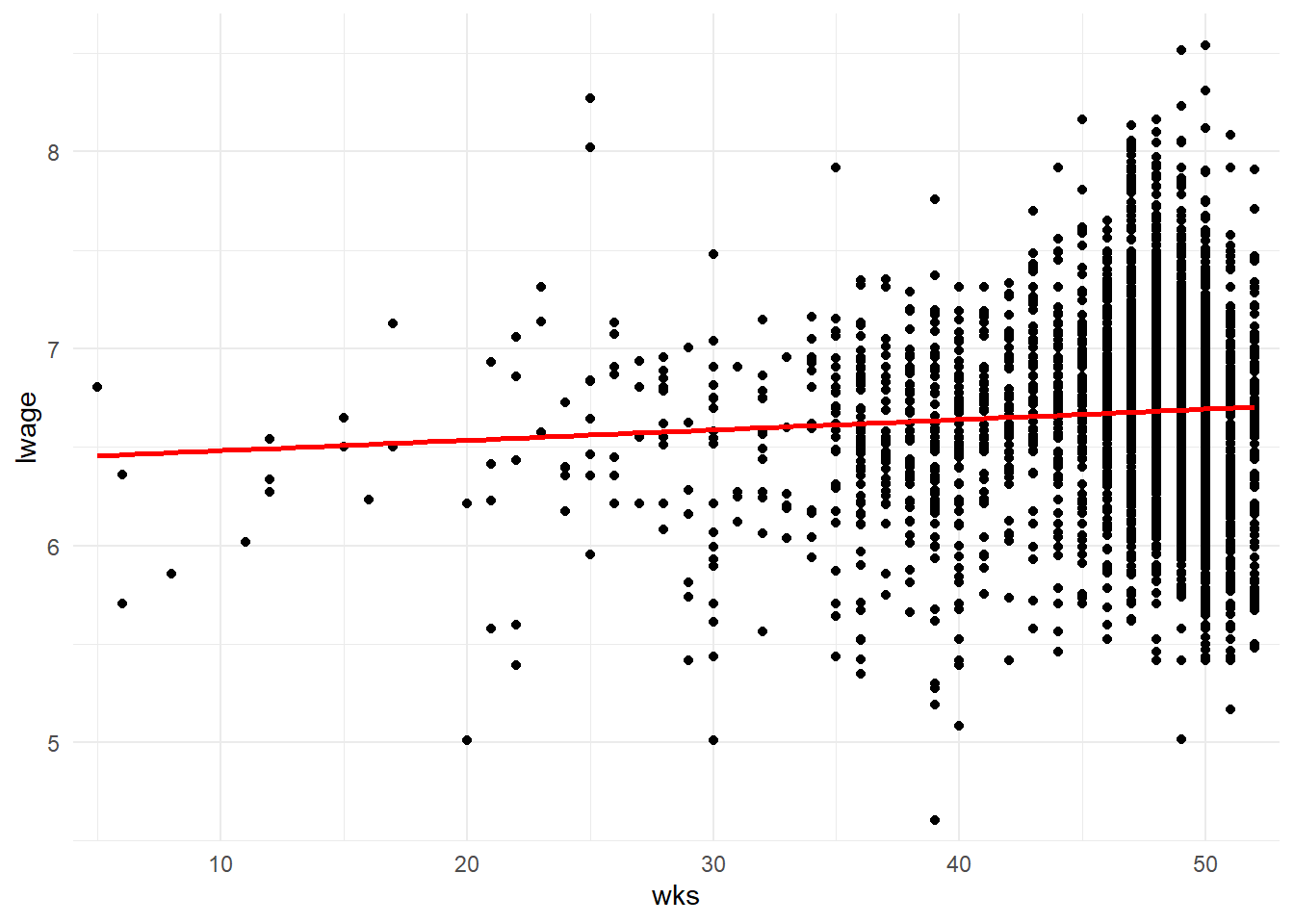
cette approche est appropriée si l’erreur uit est indépendante à la fois du régresseur xit et de sa composante individuelle de l’erreur γi (et/ou sa composante temporelle μt). Dans le cas contraire, l’estimateur de MCO est inconsistant.
Qu’est-ce que cela signifie d’un point de vue pratique? Simplement que le coefficient estimé via le pooling n’est pas différent (statistiquement) des coefficients estimés sur des bases réduites à chaque individu. Pour le savoir, on procède à un test de Chow (test de stabilité basé sur la statistique de Fisher proposé par Baltagi 2005). Le package plm offre des éléments pour réaliser la procédure. Il y a tout d’abord la fonction pvcm() qui permet de générer les estimations des modèles individus par individus (within intra-individuel).
g_i <- pvcm(lwage~wks, data=wages,index="id", model="within")
g_i$coefficients[1:20,]## (Intercept) wks
## 1 6.149891 -0.004927473
## 2 6.087555 0.013014641
## 3 7.209684 -0.013861464
## 4 6.838213 -0.009429041
## 5 5.729354 0.025000016
## 6 7.882495 -0.017218049
## 7 5.977440 0.007051670
## 8 6.241745 0.007061485
## 9 10.844273 -0.082230767
## 10 7.335141 -0.019013199
## 11 7.257963 -0.007769501
## 12 11.658995 -0.104738140
## 13 9.833990 -0.055933809
## 14 18.177601 -0.251869798
## 15 7.842392 -0.035667109
## 16 4.293681 0.035446029
## 17 8.650151 -0.036946197
## 18 -13.139425 0.438735008
## 19 6.993980 -0.008029874
## 20 16.573101 -0.195735772print("reste 575 modèles")## [1] "reste 575 modèles"Le résultat des estimations (g_i) peut alors être introduit dans la fonction pooltest() avec le résultat de l’estimation du modèle de pooling (g) pour réaliser le test.
pooltest(g, g_i)##
## F statistic
##
## data: lwage ~ wks
## F = 9.9386, df1 = 1188, df2 = 2975, p-value < 2.2e-16
## alternative hypothesis: unstabilityLe test rejette clairement l’hypothèse d’égalité de coefficients (de stabilité). Le modèle de pooling est donc inconsistant. Le même résultat peut être obtenu (plus rapidement) à partir d’une syntaxe incluant la spécification des modèles testés en lieu est place des objets associés à leur estimation.
pooltest(lwage~wks,data=wages,index='id', model = "within")##
## F statistic
##
## data: lwage ~ wks
## F = 1.7654, df1 = 594, df2 = 2975, p-value < 2.2e-16
## alternative hypothesis: unstabilityLe graphe ci-contre résume bien la situation. Y sont repris de le nuage de point et la droit du modèle de pooling mais aussi une dizaine d’autres droites (tirées au hasard) dont les paramètres sont issus des estimations individuelles.
ggplot(data=wages,aes(x=wks,y=lwage))+
geom_point()+
geom_abline(slope=g_i$coefficients[5,2],
intercept = g_i$coefficients[5,1],color='blue')+
geom_abline(slope=g_i$coefficients[55,2],
intercept = g_i$coefficients[55,1],color='blue')+
geom_abline(slope=g_i$coefficients[555,2],
intercept = g_i$coefficients[555,1],color='blue')+
geom_abline(slope=g_i$coefficients[366,2],
intercept = g_i$coefficients[366,1],color='blue')+
geom_abline(slope=g_i$coefficients[70,2],
intercept = g_i$coefficients[70,1],color='blue')+
geom_abline(slope=g_i$coefficients[66,2],
intercept = g_i$coefficients[66,1],color='blue')+
geom_abline(slope=g_i$coefficients[8,2],
intercept = g_i$coefficients[8,1],color='blue')+
geom_abline(slope=g_i$coefficients[28,2],
intercept = g_i$coefficients[28,1],color='blue')+
geom_abline(slope=g_i$coefficients[82,2],
intercept = g_i$coefficients[82,1],color='blue')+
geom_abline(slope=g_i$coefficients[43,2],
intercept = g_i$coefficients[43,1],color='blue')+
geom_smooth(method = "lm",color='red',se=FALSE)+
coord_cartesian(expand=FALSE,xlim=c(4,53),ylim=c(4.5,8.7))+
theme_minimal()## `geom_smooth()` using formula 'y ~ x'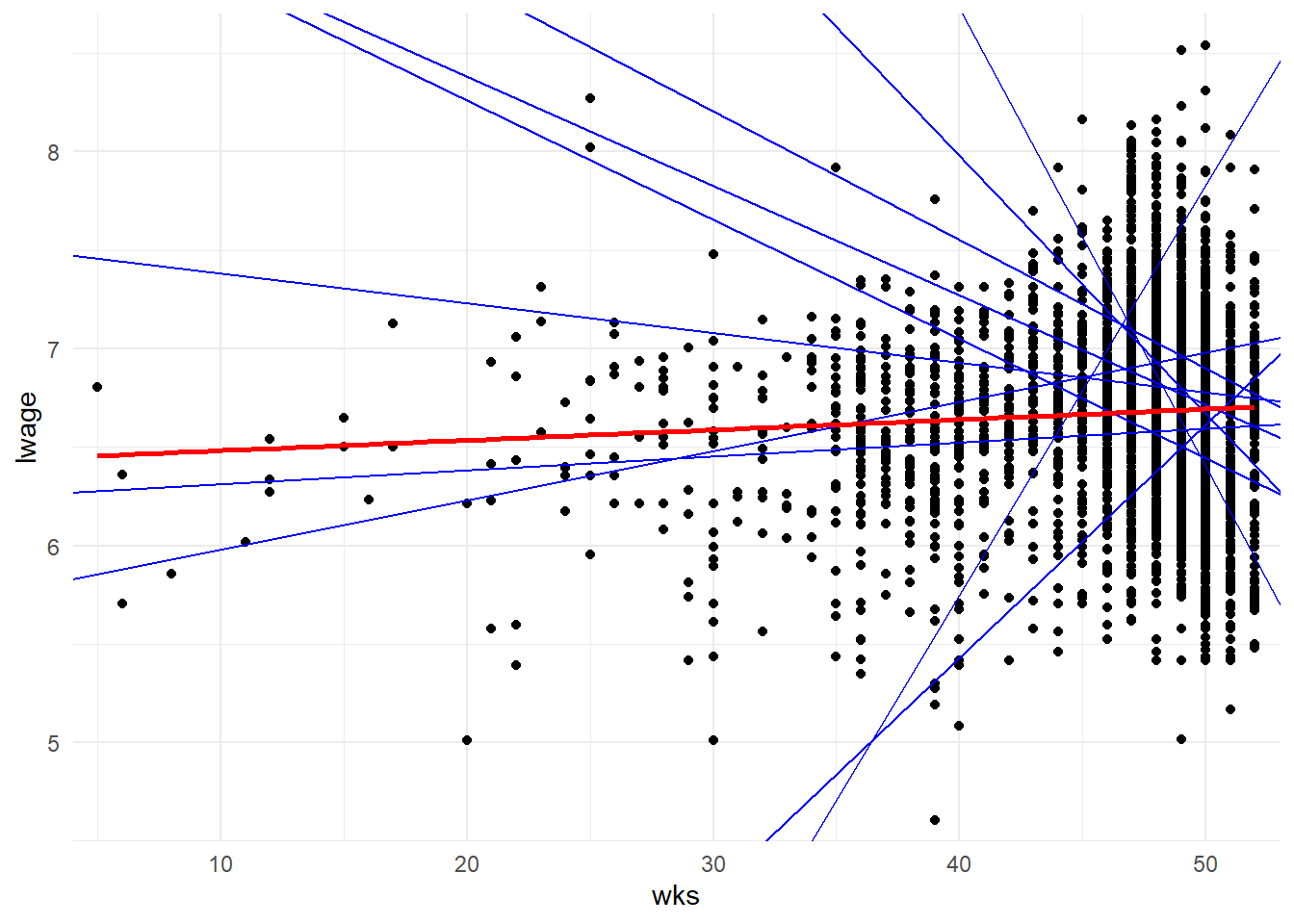
La droite en rouge résume difficilement l’information contenue dans les droites en bleu.
Un second test permet de confirmer l’existence d’un problème de variables manquantes et donc la présence d’effets à contrôler. Celui-ci est basé sur le multiplicateur de Lagrange. Il s’agit d’évaluer l’hypothèse nulle postulant que la variance inter- individus (ou période) est nulle et donc qu’il n’y a pas d’effet de panel. Le test est réalisé à partie de la fonction plmtest() de plm. Il suffit d’indiquer le modèle de pooling (ou son équation) et le type de procédure retenue. Ici, nous utiliserons la version la plus ancienne Breusch-Pagan (bp).
plmtest(g, type=c("bp"))##
## Lagrange Multiplier Test - (Breusch-Pagan) for balanced panels
##
## data: lwage ~ wks
## chisq = 5792.8, df = 1, p-value < 2.2e-16
## alternative hypothesis: significant effectsL’hypothèse d’absence d’effets de panel à prendre en compte est largement rejetée. Ce test est généralement doublé d’un second permettant de comparer le modèle de pooling (MCO simple) avec le modèle à effets fixes (“within”). La fonction pFtest() permet de le mettre en oeuvre en suivant la même type syntaxe. On peut soit indiqué les modèles à comparer avec le modèle “within” en premier et le modèle de pooling en second ou juste l’indication du premier.
pFtest(lwage~wks, data=wages,index='id', effect="individual")##
## F test for individual effects
##
## data: lwage ~ wks
## F = 16.065, df1 = 594, df2 = 3569, p-value < 2.2e-16
## alternative hypothesis: significant effectsIci aussi, l’hypothèse d’absence d’effets à prendre en compte est rejetée. Le modèle à effets fixes apparaît meilleur que le modèle de pooling.
Dans les deux cas, H0 est rejetée. Il y a bien un effet de panel. Il reste alors à déterminer qu’elle type d’effets retenir: fixes ou aléatoire.
Estimons les deux et procédons à un test de Durbin–Wu–Hausman afin de déterminer le plus pertinent.
Commençons par le modèle à effets aléatoires.
yit=α+β1.xit+μi+uit
La variabilité intra individuelle est intégrée au terme d’erreur. Il est pour cela nécessaire que l’effet soit à la fois indépendant de la variable explicative et du terme d’erreur du modèle. D’un point de vue pratique, pour l’estimer, il suffit d’utiliser la fonction plm() et de préciser “random” dans l’option model.
alea<-plm(lwage ~ wks, data=wages, index=c("id"),model="random")
alea %>% tidy()## # A tibble: 2 × 5
## term estimate std.error statistic p.value
## <chr> <dbl> <dbl> <dbl> <dbl>
## 1 (Intercept) 6.61 0.0495 134. 0
## 2 wks 0.00144 0.00100 1.44 0.150La spécification générale associée aux effets fixes individuels est la suivante:
yit=αi+β1.xit+uit
La variabilité intra individuelle est prise en compte en faisant varier l’ordonnée à l’origine de modèle. On n’a ainsi un bêta fixe et un alpha différent selon l’individu considéré. Pour l’estimer, il suffit d’utiliser la fonction plm() et de préciser “within” dans l’option model.
wit<-plm(lwage ~ wks, data=wages, index=c("id"),model="within")
wit %>% tidy()## # A tibble: 1 × 5
## term estimate std.error statistic p.value
## <chr> <dbl> <dbl> <dbl> <dbl>
## 1 wks 0.00101 0.00102 0.988 0.323Le test est réalisé à partir de la fonction phtest() en intégrant les noms des modèles à comparer.
phtest(wit,alea)##
## Hausman Test
##
## data: lwage ~ wks
## chisq = 4.3878, df = 1, p-value = 0.0362
## alternative hypothesis: one model is inconsistentLe modèle à effet aléatoire est diagnostiqué comme inconsistant. Le modèle à effet fixe apparaît ici comme le meilleur. Mais en quoi consiste-t-il au juste?
Dans sa version la plus simple, il s’agit d’une estimation par les MCO d’un modèle incluant une variable indicatrice par individu (id). Ici, on aura donc 595 variables binaire supplémentaire (moins une si on garde la constante dans le modèle).
dum_mod<-lm(lwage~wks+factor(id)-1,data=wages)
dum_mod%>% tidy()## # A tibble: 596 × 5
## term estimate std.error statistic p.value
## <chr> <dbl> <dbl> <dbl> <dbl>
## 1 wks 0.00101 0.00102 0.988 0.323
## 2 factor(id)1 5.93 0.105 56.3 0
## 3 factor(id)2 6.47 0.103 62.6 0
## 4 factor(id)3 6.46 0.111 58.3 0
## 5 factor(id)4 6.34 0.110 57.8 0
## 6 factor(id)5 6.86 0.109 62.8 0
## 7 factor(id)6 7.05 0.109 64.8 0
## 8 factor(id)7 6.26 0.109 57.3 0
## 9 factor(id)8 6.54 0.110 59.3 0
## 10 factor(id)9 6.85 0.110 62.4 0
## # … with 586 more rowsSi cette version permet bien de contrôler des effets fixes individuels et donc de l’inobservable variant en fonction de l’individu et pas dans le temp, elle reste laborieuse à manipuler. Aussi, il existe une alternative plus pratique produisant le même résultat sans les variables indicatrice individuelles : le modèle “within”. Il s’agit de transformer les variables en leur soustrayant leur moyenne calculé sur une base individuel et d’appliquer les MCO sur le résultat de la transformation. On a ainsi:
(yit−¯yi)=αi+β1.(xit−¯xi)+(uit−¯ui)
Réalisons la transformation “within” sur nos données.
wi_d<-wages %>% group_by(id) %>%
mutate(m_lwage=mean(lwage),m_wks=mean(wks),
w_lwage=lwage-m_lwage,w_wks=wks-m_wks)Estimons le modèle à partir de la fonction lm().
w_l<-lm(w_lwage~w_wks-1,data=wi_d)
w_l %>% tidy()## # A tibble: 1 × 5
## term estimate std.error statistic p.value
## <chr> <dbl> <dbl> <dbl> <dbl>
## 1 w_wks 0.00101 0.000945 1.07 0.286On retrouve bien le même coefficient estimé que dans la version intégrant les variables indicatrices individuelles et dans celle générée à partir de plm(.,model=“within”). Par contre, l’erreur standard est différente. Voyons ce qu’il en est. Commençons par recalculer en détaillant les différentes étapes la statistique pour nos différents modèle.
Voyons d’abord par le dernière modèle. Mais avant, un petit rappel. Le point de départ pour obtenir l’erreur standard des coefficients est la matrice variance covariance du modèle (var(ˆβ)).
VAR(ˆβ)=ˆσ2.(X′.X)−1
Celle-ci est diagonalisée et passée à la racine carrée.
s.e.(ˆβ)=√diag(VAR(ˆβ))
La fonction vcoc() permet d’obtenir la matrice à partir du modèle.
vcov(w_l)## w_wks
## w_wks 8.929782e-07Mais on peut aussi détailler le calcul permettant d’obtenir ce résultat
invXtX <- solve(crossprod(wi_d$w_wks))
(sum(w_l$residuals^2)/(w_l$df.residual))*invXtX## [,1]
## [1,] 8.929782e-07Reste à diagonaliser et passer l’ensemble à la racine carré.
sqrt(diag(vcov(w_l)))## w_wks
## 0.0009449752On retrouve bien notre erreur standard. Voyons ce qu’il en est avec les deux autres modèles.
c(sqrt(diag(vcov(wit))),sqrt(diag(vcov(dum_mod)))[1])## wks wks
## 0.00102071 0.00102071Nous avons retrouvons bien les mêmes erreurs standards. Ceci étant posé, il nous reste à comprendre comment le modèle “within” ajuste les choses pour produire la même valeur le modèle à variables indicatives. En fait, il va ajuster sa matrice variance covariance de manière à ce que les mêmes restrictions en matière de degrés de liberté des résidus soit considéré. Pour rappel, dans le modèle dum_mod nous avons un paramètre par individu donc 595 et un paramètre pour wks. On a donc 4165-596 degrés de liberté soit 3569.
invXtX<-solve(crossprod(wi_d$w_wks))
var_b<-(sum(w_l$residuals^2)/(3569))*invXtX
sqrt(diag(var_b))## [1] 0.00102071Bon voilà, je pense que ce premier poste est déjà assez long. (suite au prochain numéro… On tient peut être là une série estivale? qui sait?)