Le premier contact avec une interface de programmation des lycéens de mon époque (le début des années 90) se limitait à la prise en main de calculatrices programmables (TI80 ou Casio Graph…). Nous l’utilisions principalement pour réaliser des tracés de fonctions de manière à vérifier les résultats des calculs que nous effectuions manuellement. Bon,il est vrai que certains y stockaient des antisèches ou y codaient des jeux vidéo rudimentaires (casse-briques, space invaders…). Mais, ce n’était pas mon cas. En fait, l’outil ne m’intéressait pas beaucoup (et c’est encore un peu le cas). Pour l’anecdote, j’ai appris que l’on pouvez y stocker des informations textuelles en déjeunant avec des amis une heure avant d’aller passer l’épreuve de mathématiques du BAC… Il était alors trop tard pour commencer à tricher et heureusement je n’en ai jamais eu besoin. A l’époque, les machines, compte tenue de leur faible puissance, fonctionnaient uniquement avec un langage dédié assez rudimentaire. Les modèles plus récents intègrent des langages script modernes comme Python. Aussi, je me suis demandé récemment si les applications que j’utilisais alors, et que mes étudiants utilisent aujourd’hui en analyse, pouvaient être répliquées avec R. Voyons ce qu’il en est.
Même s’il n’a pas été conçu pour les mathématiques en générale, mais pour les statistiques en particulier (qui en sont une branche), R base propose certaines fonctionnalités permettant ce type de traitement. Celles-ci sont d’ailleurs complétées et améliorées par des Packages dédiés à la résolution de certains problèmes types. Commençons notre exploration par la seule chose que je faisais à l’époque avec ma Casio.
Tracer les courbes des fonctions étudiées
La commande function(){} permet d’encapsuler un élément de code dans un objet dédié afin pouvoir le rappeler ultérieurement en utilisant juste le nom attribué accompagné des arguments nécessaire à son fonctionnement. Cette technique peut être mobilisée dans le cadre d’exercices d’analyse. Il suffit d’indiquer l’expression mathématique étudiée comme corps de la fonction. Illustrons cela au travers d’un exemple simple:
f(x)=x2
Intégrons l’expression dans une fonction R. Celle-ci prend un seul argument la valeur de la variable x et l’élève au carré.
f_<-function(x) x^2On a donc pour une valeur de x égale à 2 (évidemment cela marche aussi pour des fonctions plus compliquées mais disons que je manque d’imagination) f(x)=4.
f_(2)## [1] 4On peut profiter du fonctionnement vectoriel de R pour très rapidement évaluer la fonctions pour plusieurs valeurs de x.
f_(-3:3)## [1] 9 4 1 0 1 4 9Présentons cela au travers d’un tableau.
x<--3:3
tab<-rbind(x,f_(x));rm(x)
row.names(tab)<-c('x','f_(x)')
colnames(tab)<-rep('',7)
tab##
## x -3 -2 -1 0 1 2 3
## f_(x) 9 4 1 0 1 4 9Ces facultés de calcul rapide sont exploités pour établir le graph de la fonction. Cela est réalisé dans R base au travers de la commande curve() qui prend comme premier argument le nom (ici f_) ou l’énoncé de la fonction et comme arguments suivant les bornes de l’intervalle sur lequel elle sera tracée (from= -3,to=3).
curve(f_,from=-3, to=3)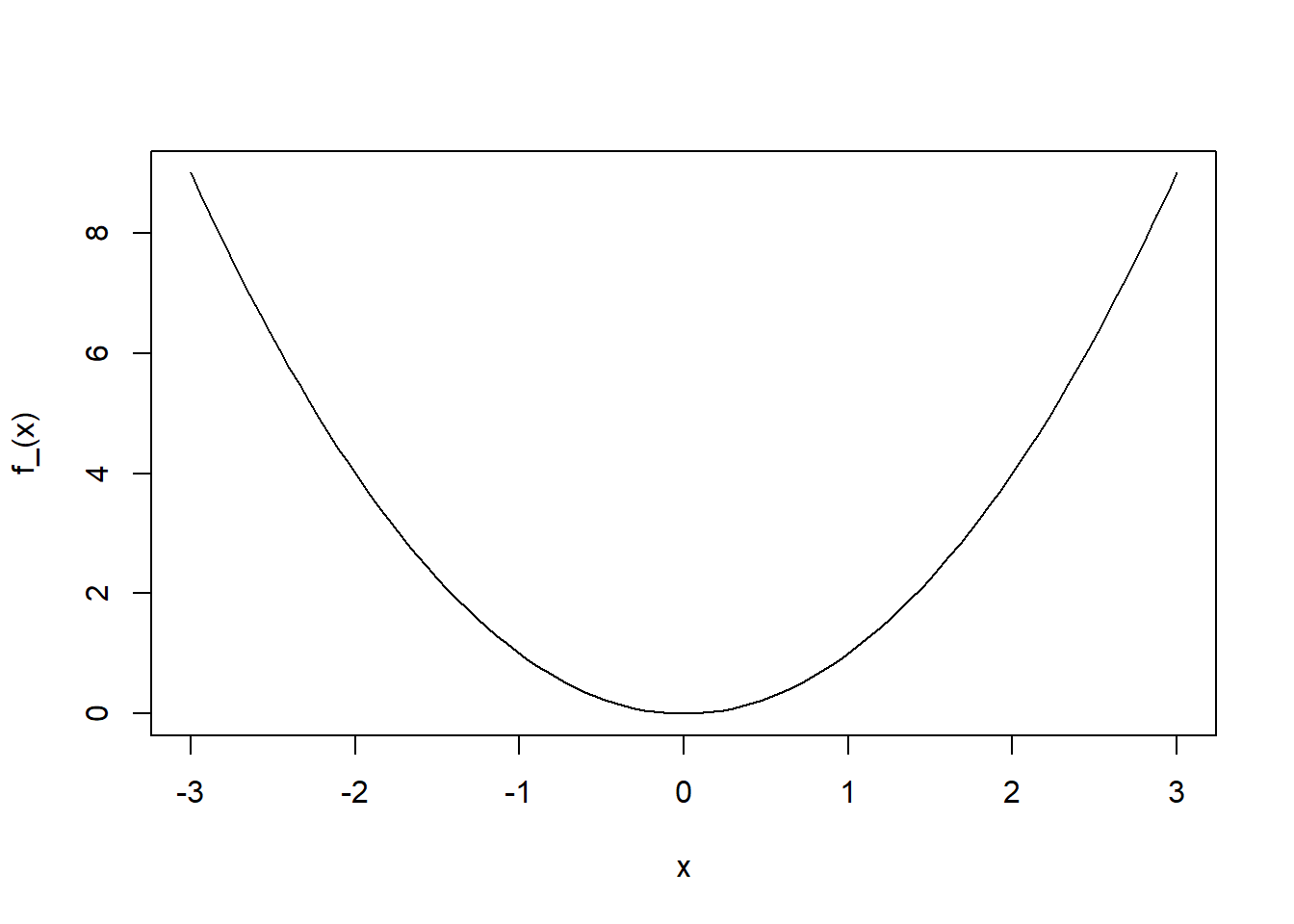
On obtient bien une parabole. Celle-ci est tracée dans le repaire classique des graphes R avec les axes sur la gauche et en bas et une graduation différente pour chacun d’eux.
Voyons ce qu’il est possible de faire pour obtenir quelque chose de visuellement plus plaisant avec GGPLOT2. Chargeons le via le tidyverse. Puis, créons un graphe en désignant la page de valeur de x sur lequel la fonction va être tracée celle-ci étant appelée à l’aide du geom_function().
library(tidyverse)
ggplot() + xlim(-3,3) + geom_function(fun = f_)
Essayons de rapprocher le graphe de celui obtenu via une calculatrice. Commençons par ajuster le thème pour quelque chose de plus simple (theme_minimal())et colorons en rouge la courbe de notre fonction.
ggplot() + xlim(-3, 3) +
geom_function(fun = f_,color='red')+
theme_minimal()+
theme(panel.grid.major=element_line(color='#E5E7E9'))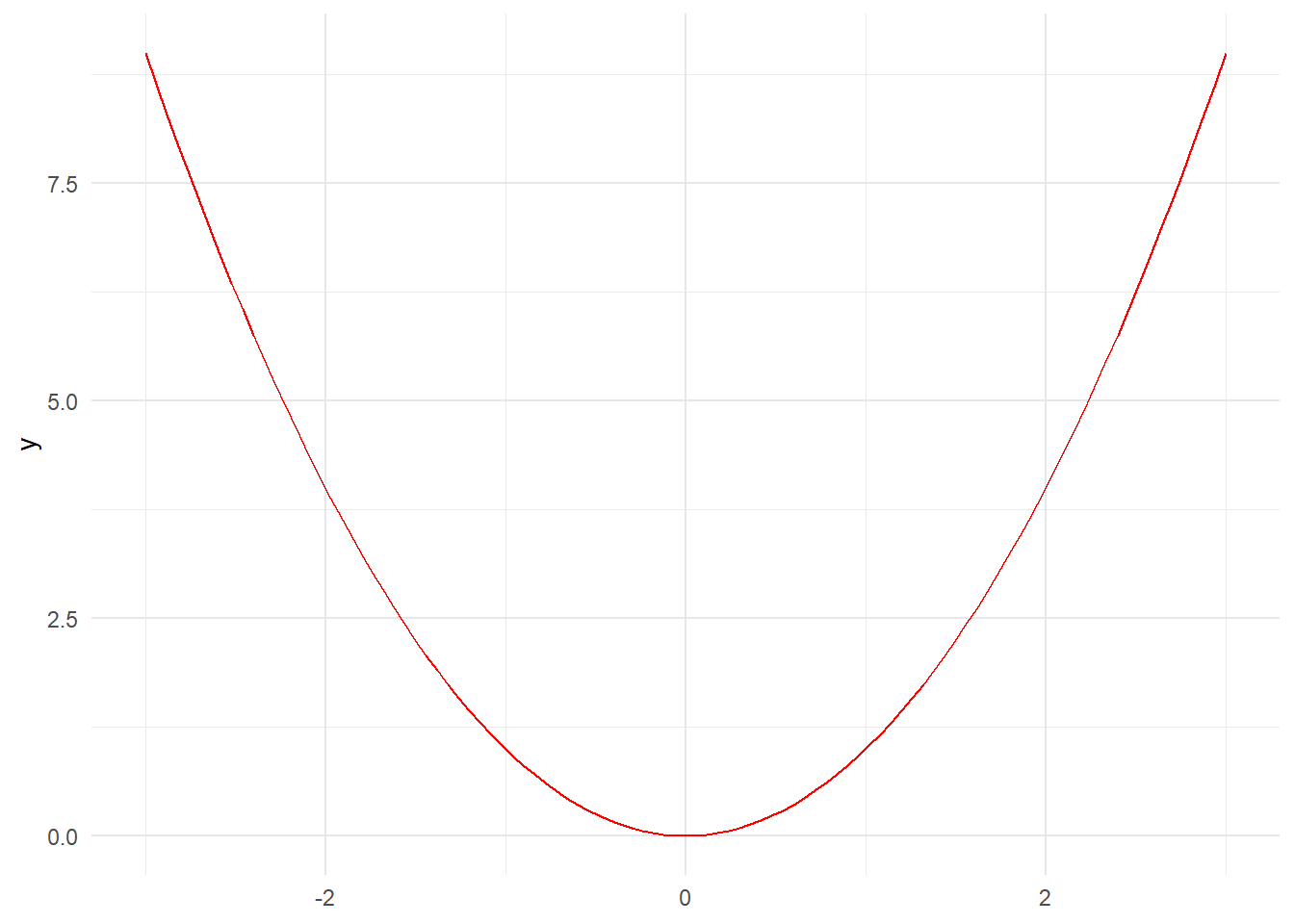
Ajustons l’ensemble pour obtenir une courbe centré dans une repaire orthonormé (avec des graduations équivalentes dans les deux dimensions). Pour cela, étendons la fenêtre d’estimation (-9:9) et zoom sur les valeurs de x et f(x) sur l’intervalle d’origine (-3:3).
ggplot() + xlim(-9, 9) +
geom_hline(yintercept=0)+
geom_vline(xintercept=0)+
geom_function(fun = f_,color='red')+
coord_cartesian(xlim=c(-9,9),ylim=c(-9,9),expand=FALSE)+
theme_minimal()+
theme(panel.grid.major=element_line(color='#E5E7E9'),
panel.grid.minor=element_line(color='#F8F9F9'),
axis.title.x = element_blank(),
axis.title.y = element_blank())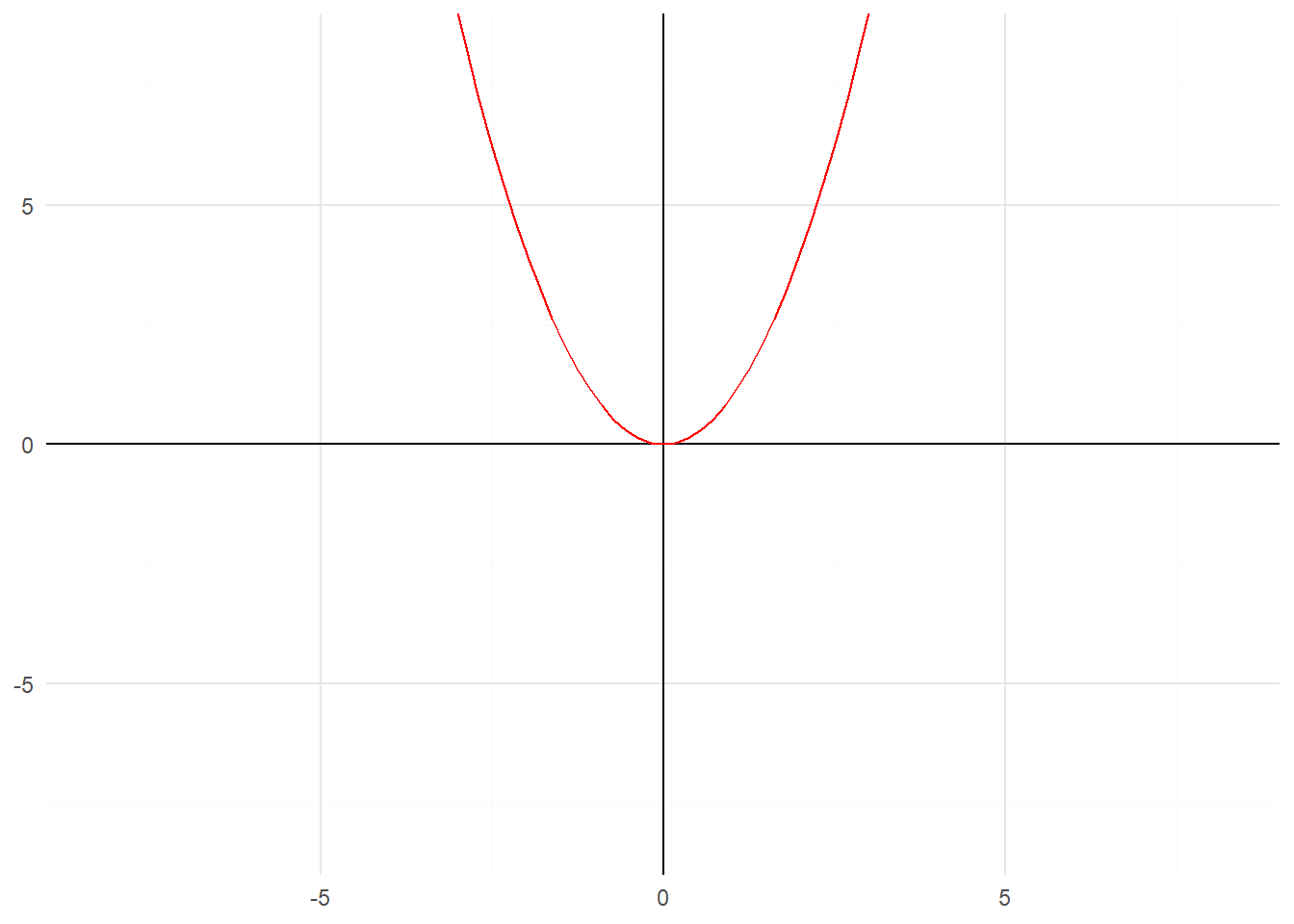
Ajoutons des éléments textuels pour habiller les axes et nommer la courbe. Pour cela, utilisons le geom_richtext() proposé par le package ggtext.
library(ggtext)
ggplot() + xlim(-9, 9) +
geom_hline(yintercept=0)+
geom_vline(xintercept=0)+
geom_function(fun = f_,color='red')+
geom_richtext(aes(x=0.2,y=8.7),label='*y*',family='serif',
fill = NA, label.color = NA)+
geom_richtext(aes(x=8.7,y=-0.2),label='*x*',family='serif',
fill = NA, label.color = NA)+
geom_richtext(aes(x=4,y=8),label='*f(x)=x^2*',family='serif',
fill = NA, label.color = NA,color='red')+
coord_cartesian(xlim=c(-9,9),ylim=c(-9,9),expand=FALSE)+
theme_minimal()+
theme(panel.grid.major=element_line(color='#E5E7E9'),
panel.grid.minor=element_line(color='#F8F9F9'),
axis.title.x = element_blank(),
axis.title.y = element_blank())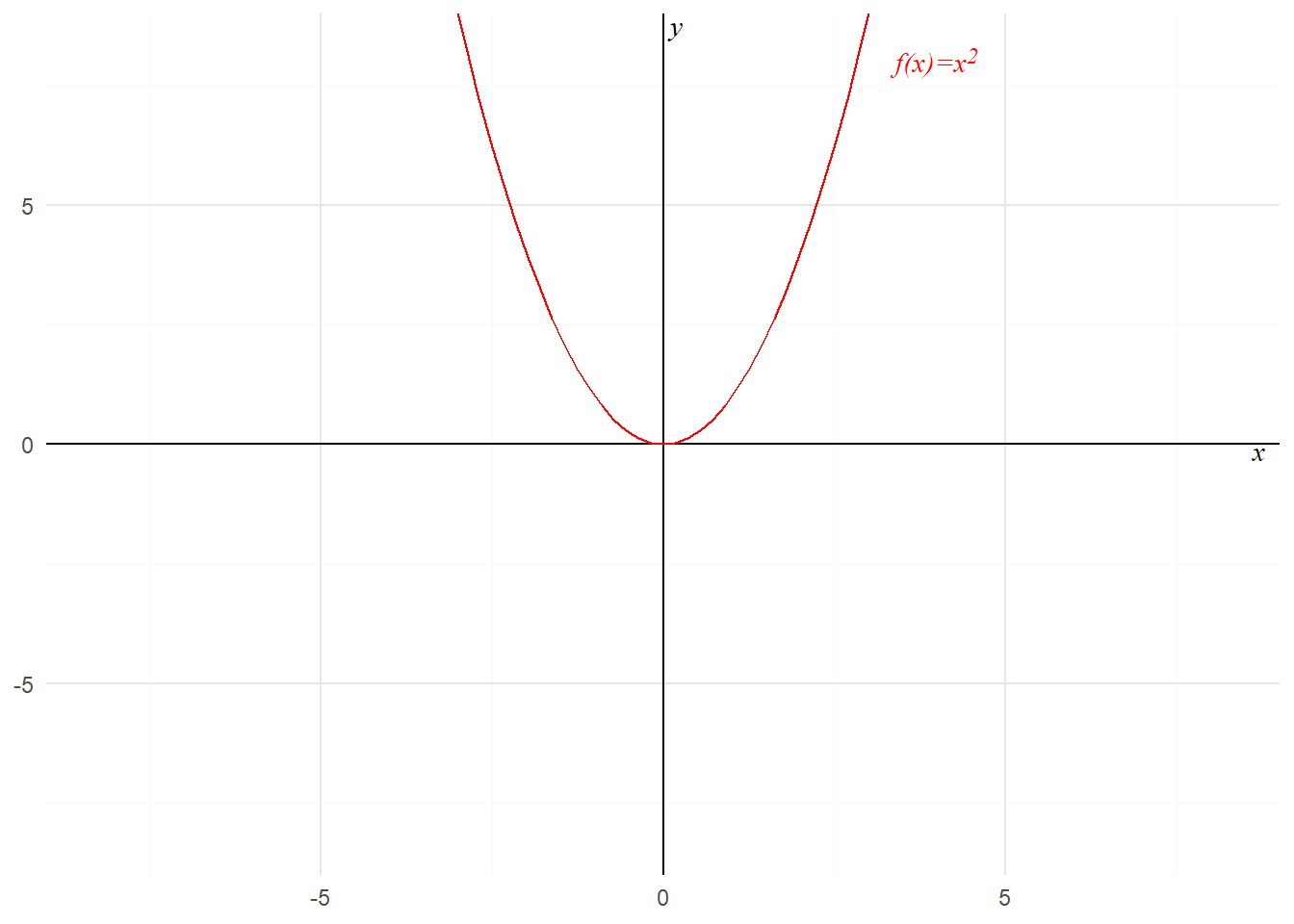
On peut sans difficultés représenter plusieurs fonctions sur le même graphe. Ajoutons au notre la courbe de :
g(x)=x3−2
g_<-function(x) x^3-2
ggplot() + xlim(-9, 9) +
geom_hline(yintercept=0)+
geom_vline(xintercept=0)+
geom_function(fun = f_,color='red')+
geom_function(fun = g_,color='blue')+
geom_richtext(aes(x=0.2,y=8.7),label='*y*',family='serif',
fill = NA, label.color = NA)+
geom_richtext(aes(x=8.7,y=-0.2),label='*x*',family='serif',
fill = NA, label.color = NA)+
geom_richtext(aes(x=4,y=8),label='*f(x)=x^2*',family='serif',
fill = NA, label.color = NA,color='red')+
geom_richtext(aes(x=1,y=8),label='*g(x)=x^3 - 2*',family='serif',
fill = NA, label.color = NA,color='blue')+
coord_cartesian(xlim=c(-9,9),ylim=c(-9,9),expand=FALSE)+
theme_minimal()+
theme(panel.grid.major=element_line(color='#E5E7E9'),
panel.grid.minor=element_line(color='#F8F9F9'),
axis.title.x = element_blank(),
axis.title.y = element_blank())
Le résultat obtenu pour les fonctions polynomiales avec geom_function() sont assez satisfaisant mais qu’en est-il pour une fonction rationnelle dont le graphe est une hyperbole? Voyons cela avec :
z(x)=1x
z_<-function(x) 1/x
ggplot() + xlim(-9, 9) +
geom_hline(yintercept=0)+
geom_vline(xintercept=0)+
geom_function(fun = z_,color='red')+
geom_richtext(aes(x=0.2,y=8.7),label='*y*',family='serif',
fill = NA, label.color = NA)+
geom_richtext(aes(x=8.7,y=-0.2),label='*x*',family='serif',
fill = NA, label.color = NA)+
geom_richtext(aes(x=1,y=8),label='z(x)=1/x)',family='serif',
fill = NA, label.color = NA,color='red')+
coord_cartesian(xlim=c(-9,9),ylim=c(-9,9),expand=FALSE)+
theme_minimal()+
theme(panel.grid.major=element_line(color='#E5E7E9'),
panel.grid.minor=element_line(color='#F8F9F9'),
axis.title.x = element_blank(),
axis.title.y = element_blank())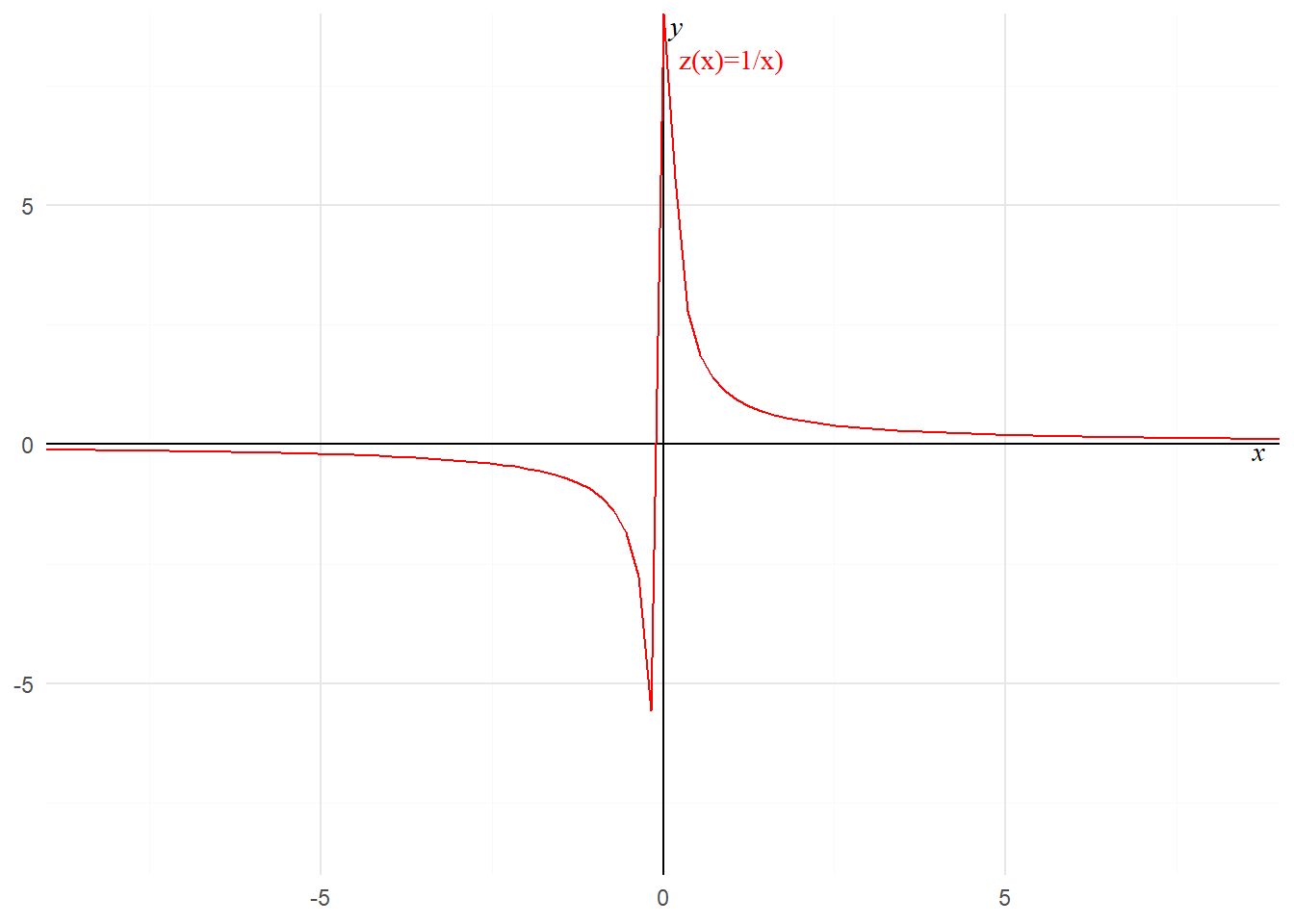
La présentation est loin d’être satisfaisante (ici le résultat obtenu avec la fonction curve() est meilleure…). Elle fait apparaître des valeurs de z(x) qui n’existent pas en reliant arbitrairement les valeurs de z(x) quand x tend vers 0. Cette difficulté peut être surmonté en utilisant à la place du geom_function(), qui donne un tracé continu, la commande stat_function(). Elle permet de désigner le type de geom que l’on veut mobiliser pour représenter les valeurs de la fonction. Choisissons ici des points. Indiquons que l’on veut en avoir suffisamment pour donner l’illusion d’une continuité des valeurs (200000). Profitons de l’opération pour présenter de manière plus adéquate le texte associé à la fonction z(x). Pour cela, utilisons le package latex2exp et sa fonction TeX().
library(latex2exp)
ggplot() + xlim(-9, 9) +
geom_hline(yintercept=0)+
geom_vline(xintercept=0)+
stat_function(fun = z_,color='red',geom = "point", n = 200000,
size=0.01)+
geom_richtext(aes(x=0.2,y=8.7),label='*y*',family='serif',
fill = NA, label.color = NA)+
geom_richtext(aes(x=8.7,y=-0.2),label='*x*',family='serif',
fill = NA, label.color = NA)+
geom_text(aes(x=1,y=8),label=TeX("$z(x)=\\frac{1}{x}$"),family='serif',
fill = NA, label.color = NA,color='red')+
coord_cartesian(xlim=c(-9,9),ylim=c(-9,9),expand=FALSE)+
theme_minimal()+
theme(panel.grid.major=element_line(color='#E5E7E9'),
panel.grid.minor=element_line(color='#F8F9F9'),
axis.title.x = element_blank(),
axis.title.y = element_blank())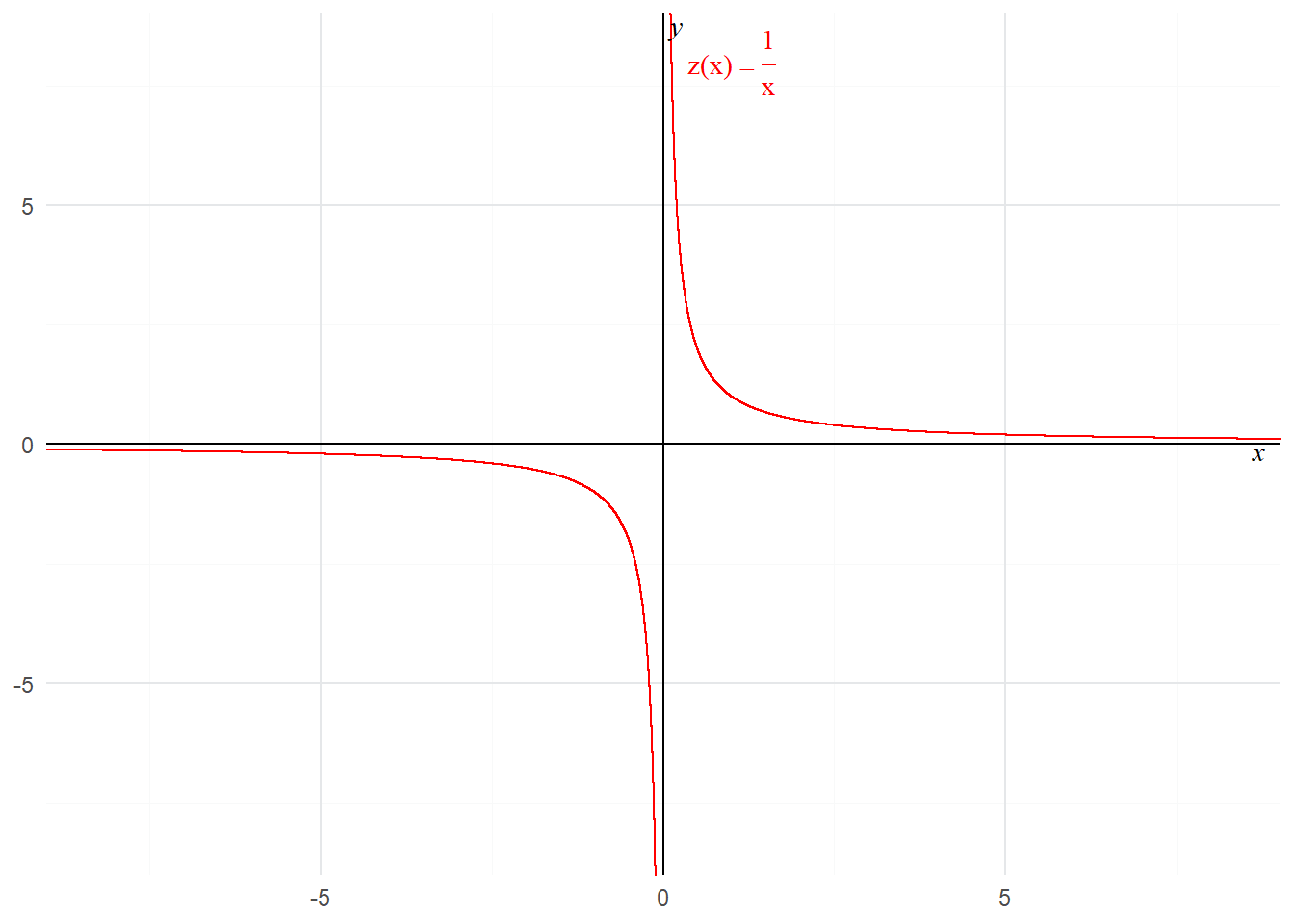
Résolution algébrique
Les propriétés des courbes des fonctions étudiées peuvent se déduire sans recourir au tracé à l’aide de différents calculs et là aussi R peut être mobilisé. Même si ici encore, il apparaît moins pratique que les logiciels spécialisés dans le calcul symbolique de type Mathlab, Mapple…
Dérivation
Rappelons qu’une fonction est croissante sur un intervalle si et seulement si sa dérivée est positive sur le dit intervalle. Elle est décroissante si et seulement si celle-ci est négative.
La commande D() permet d’obtenir cette dérivé directement. Elle prend comme argument un objet de type expression et comme second la désignation de la variable par rapport à laquelle la dérivée sera établie. Cela permet de générer les dérivées partielles des fonctions à plusieurs variables.
Illustrons son utilisation sur f_. Rappelons son contenu avec la commande body() et assurons-nous qu’il soit au format expression en le passant à as.expression().
f_prim<-body(f_) %>% as.expression() %>% D('x')
f_prim## 2 * xLe résultat est donné sous une forme qui n’est pas toujours pratique.
Extremum(s)
Il s’agit de points autour desquels la variation de la courbe change. Elle passe de croissante à décroissante ou de décroissante à croissante. Pour le déterminer, il suffit de trouver la valeur de la variable permettant d’annuler la dérivée de la fonction.
R propose différentes solutions pour résoudre différents types d’équations et système d’équations. Je n’en retiendrai ici qu’une seule: le package Ryacas. Celui-ci introduit les fonctionnalités du logiciel (gratuit) de calcules yacas (Yet Another Computer Algebra System). Il offre énormément de flexibilité dans les traitements réalisés.
Utilisons sa commande solve() sur notre dérivée de f_. Pour ce faire, nous devenons au préalable indiquer que x doit être considéré comme un symbole et non comme un vecteur de valeur dans les calculs réalisés. Cela se fait à l’aide de la commande ysum().
library(Ryacas)
f_prim %>% as.expression() %>% ysym() %>% solve('x')## {x==0}Notre dérivée s’annule en x=0. On a un extremum en 0.
Bon, ici les choses ne sont pas très spectaculaires. La fonction est bien trop simple (je manque d’imagination). Je laisse au lecteur le loisir de s’amuser avec des exemples plus élaborer. Mais avant, voyons quelques applications de fonctionnalité du package qui peuvent s’avérer utiles.
- développer une expression avec la fonction y_fn() et l’option Expand.
x<-ysym('x')
y_fn((x-1)^5,'Expand')## y: x^5-5*x^4+10*x^3-10*x^2+5*x-1Attention la déclaration de x comme élément symbolique yacas et non comme vecteur est important lorsque l’on utilise ce type de commandes.
- factoriser une expression avec la fonction y_fn() et l’option Factor.
x^5-5*x^4+10*x^3-10*x^2+5*x-1 %>% y_fn('Factor')## y: x^5-5*x^4+10*x^3-10*x^2+5*x-1- simplifier une expression avec la fonction simplify().
"(x^2-1)/(x-1)" %>% ysym() %>% simplify()## y: x+1- les résultats obtenus à l’aide d’une de ces fonctions peut-être rendu au format latex en utilisant dessus la fonction tex().
(2*(1+4*x^2+4))/((2-2*x)^2) %>% simplify() ## y: (4*x^2+5)/(2*(x^2-2*x+1))tex(simplify((2*(1+4*x^2+4))/((2-2*x)^2)))## [1] "\\frac{4 x ^{2} + 5}{2 \\left( x ^{2} - 2 x + 1\\right) }"Maximum ou minimum
Pour savoir si le ou les points identifiés comme des extremums sont des minimums ou des maximums. Il faut établir le sens de variation de la fonction avant et après celui-ci. Il s’agit d’un minimum si avant la fonction décroissante puis après elle est croissante. Il s’agit d’un maximum si avant la fonction est croissante puis après elle est décroissante.
Dans le premier cas, la fonction est convexe. Sa dérivée est négative avant le point et positive après. Sa dérivée seconde est positive. Dans le second cas, la fonction est concave. Sa dérivée est positive avant et négative après. Sa dérivée seconde est négative.
Pour obtenir cette dérivée seconde, il suffit d’appliquer la commande D() en série (deux fois). Illustrons les choses avec notre fonction f_.
body(f_) %>% as.expression() %>% D('x') %>% D('x') ## [1] 2La dérivée seconde de f_ est une constante positive (2). La fonction est donc convexe sur l’ensemble des ses valeurs. Le point x égale 0 est un minimum.
Points d’inflexion
La fonction peut également établir un autre type de points remarquables les points d’inflexion. Ils marquent les changements de concavité de la fonction. On les identifie en annulant la dérivée seconde.
Ici, on ne peut pas utiliser f_ pour illustrer la procédure 2, sa dérivée seconde est une constante. Travaillons donc avec g_ (g(x)=x3). Commençons par établir sa dérivée seconde. Assurons-nous qu’elle soit présentée sous forme simplifiée.
g_sec<-body(g_) %>% as.expression() %>% D('x') %>% D('x') %>%
as.expression() %>% ysym() %>% simplify()
g_sec## y: 6*xReste alors à rechercher la valeur de x permettant d’annuler cette expression.
g_sec %>% solve('x')## {x==0}Le point pour lequel x=0 est l’unique point d’inflexion de g_ celui qui fait passer la fonction d’une forme concave à une forme convexe ou inversement. Pour déterminer, il suffit d’observer le signe de la dérivée seconde avant et après le point d’inflexion. Faisons-le à partir d’une série de valeur de x avant et après et injectons les dans notre expression de g_sec. Attention, celle-ci est au format liste. Il faut donc procéder à quelques transformations pour réaliser l’opération (bon, il est vrai qu’on aurait pu simplement recopier la dérivée seconde pour les besoins du calcul… mais c’est plus drôle comme ça. Non?)
x<--2:2
E <- function (...) {eval(parse(text=paste(...,collapse=" ")))}
E(g_sec$yacas_cmd)## [1] -12 -6 0 6 12On va bien que la dérivée seconde de g_ est négative avant 0 et positive après. Elle est donc concave avant 0 et convexe après.
Limites
Souvent exercices d’étude fonction se complétaient d’établissement de leur valeurs limite. Ryacas permet également de les déterminer très facilement avec la commande lim(). Illustrons son utilisation avec la f_.
limx→−∞f(x)=?
x<-ysym('x')
f_ %>% body() %>% as.expression() %>% ysym() %>% lim('x',-Inf)## y: Infinitylimx→−∞f(x)=+∞
limx→0+f(x)=?
f_ %>% body() %>% as.expression() %>% ysym() %>% lim('x',0,from_left=TRUE)## y: 0limx→0+f(x)=0
limx→0−f(x)=?
f_ %>% body() %>% as.expression() %>% ysym() %>% lim('x',0,from_right=TRUE)## y: 0limx→+∞f(x)=0
f_ %>% body() %>% as.expression() %>% ysym() %>% lim('x',+Inf)## y: Infinitylimx→+∞f(x)=+∞
Quelle Conclusion peut-on tirer de tous cela? On peut réaliser sans grandes difficultés réaliser des exercices d’analyse de seconde avec R, mais qui en doutait? Nous utiliserons ces différentes fonctionnalités dans de prochains post sur des problèmes et applications plus complexes (et intéressants). A suivre…